第2章 时域离散信号和系统的频域分析(12上).ppt

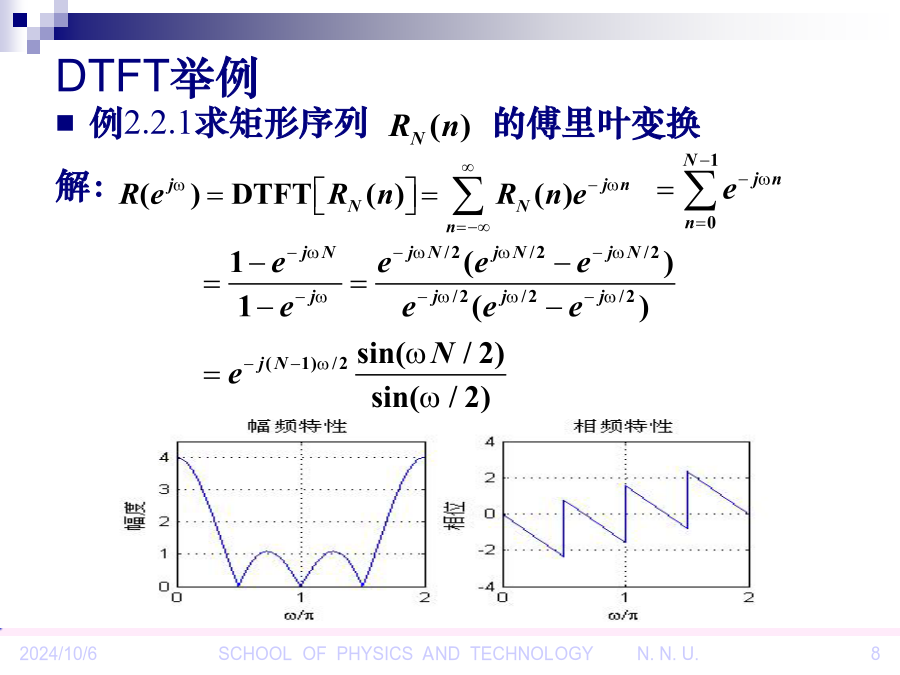
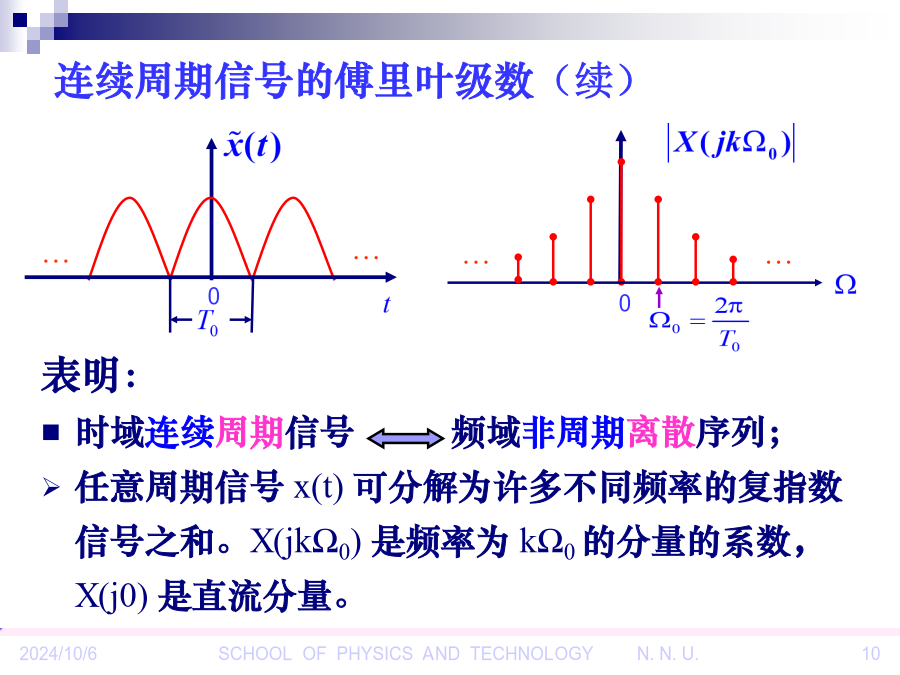
第2章时域离散信号和系统的频域分析本章主要内容2.1引言2.2时域离散信号的傅里叶变换连续信号的傅里叶变换（FT）2.2.1时域离散信号的傅里叶变换的定义反变换（IDTFT）定义：

证明：

由于

于是DTFT举例2.2.2周期信号的离散傅里叶级数（DFS）表明：
时域连续周期信号频域非周期离散序列；
任意周期信号x(t)可分解为许多不同频率的复指数信号之和。X(jkΩ0)是频率为kΩ0的分量的系数，X(j0)是直流分量。周期序列的离散傅里叶级数（DFS）周期序列的离散傅里叶级数（续）k、n均取整数；是周期函数，周期为N
是周期为N的周期序列，即
令

则：离散傅里叶级数（DFS）对：周期序列的离散傅里叶级数（续）例2.2.2设，将以N=8为周期进行周期延拓，得到周期序列，试求的离散傅里叶级数的系数得：四种傅立叶变换:四种傅立叶变换2.2.3周期信号的傅里叶变换1.复指数序列的傅里叶变换复指数序列的傅里叶变换（续）求证：2.一般周期序列的傅里叶变换一般周期序列的傅里叶变换（续）例2.2.3设，将以N=8为周期进行周期延拓，得到周期序列，试求的傅里叶变换幅频特性：例2.2.4令，为有理数，求其傅里叶变换。余弦信号的傅里叶变换是在处的冲激函数；强度为；以为周期进行周期性延拓。正弦序列，为有理数，求其傅里叶变换。基本序列的傅里叶变换[P/31]2.2.4时域离散信号傅里叶变换的性质周期性的意义
对信号进行频域分析时，只需分析一个周期即可；
在处，表示直流分量；
在附近为低频分量
在附近为高频分量2.时域卷积定理证明该定理说明，两序列卷积的DTFT，结果服从相乘的关系。
对于线性时不变系统输出的DTFT，等于输入信号的DTFT乘以单位脉冲响应的DTFT。因此求系统的输出信号，可以在时域用卷积公式计算，也可以在频域按照前式作乘积，求出输出的DTFT，再作IDTFT求出输出信号。3.频域卷积定理证明例2.2.5设，
求的傅里叶变换。2024/10/63.傅里叶变换的对称性傅里叶变换的对称性（续）序列分解为实部和虚部——纯虚数序列的傅里叶变换具有共轭反对称性质因如果将序列傅里叶变换写成：小结：2.3时域离散信号的Z变换Z变换的意义Z变换的意义2.3.1Z变换的定义及其与傅里叶变换的关系Z变换的定义（续）得到：2.Z变换与离散时间傅里叶变换之间的关系Table3.8:Somecommonlyusedz-transformpairs.2.3.2Z变换的收敛域与序列特性之间的关系1.有限长序列Z变换的收敛域2.右边序列Z变换的收敛域3.左边序列Z变换的收敛域4.双边序列Z变换的收敛域例：2.3.2求的Z变换及其收敛域例：2.3.3求的Z变换及其收敛域例：2.3.4求的Z变换及其收敛域收敛域包含单位圆，其傅里叶变换存在，可直接求出2.3.3逆Z变换1.幂级数法（长除法）例：2.部分分式法部分分式法的一种计算方法：对X(z)仅有单阶极点的情况，可用留数方法求得部分分式。例2.3.5用部分分式法求逆Z变换双边序列
3.围线积分法若为单阶极点（单重极点），则多阶极点留数的计算比较麻烦，可以改求围线以外的极点的留数之和。
如F(z)在z平面上有N个极点，围线c内有个，围线c外有个围线积分的计算例子：F(z)的极点为，被围线c包围，于是例2.3.7所以2024/10/62024/10/62024/10/62024/10/62.3.4Z变换的性质线性2.3.4Z变换的性质(1)解：序列移位解：时间反转2.3.4Z变换的性质(4)微分解：利用微分性质，将非有理函数转换成有理函数表达式2.3.4Z变换的性质(6)2.3.4Z变换的性质(7)解：因为输入输出序列都为因果序列，n≥0，围线包围2个极点z=a，1，所以复卷积定理解（1）：直接简单求解方法是分别求出x(n)和y(n)，相乘后再作Z变换。V平面上的收敛域因此，V平面上的收敛域V平面上的极点W(z)的收敛域初值定理x(n)为因果序列，X(z)在单位圆上只能有一个一阶极点，其它极点均在单位圆内。2.3.4Z变换的性质(10)补充:序列的Z变换与连续时间信号的Laplace变换、Fourier变换的关系理想抽样信号的Laplace变换其Z变换：Z平面：（极坐标）单位圆外部S平面到Z平面的
映射是多值映射。2024/10/62.4利用Z变换对信号和系统进行分析Z变换域分析的意义2.4.1系统的传输函数和系统函数系统的传输函数的意义（1）输出信号的频谱取决于输入信号的频谱特性和系统的传输函数
这里仍然起着改变输入信号频谱结构的作用，因此又将称为系统的“频率响应函数”
设计不同的频率响应函数，可以实现对信号的放大、滤波、相位均衡等功能。系统函数2.4.2根据系统函数极点的分布分析系统的因果性和稳定性A影响输