《概率论与数理统计》第15讲.ppt

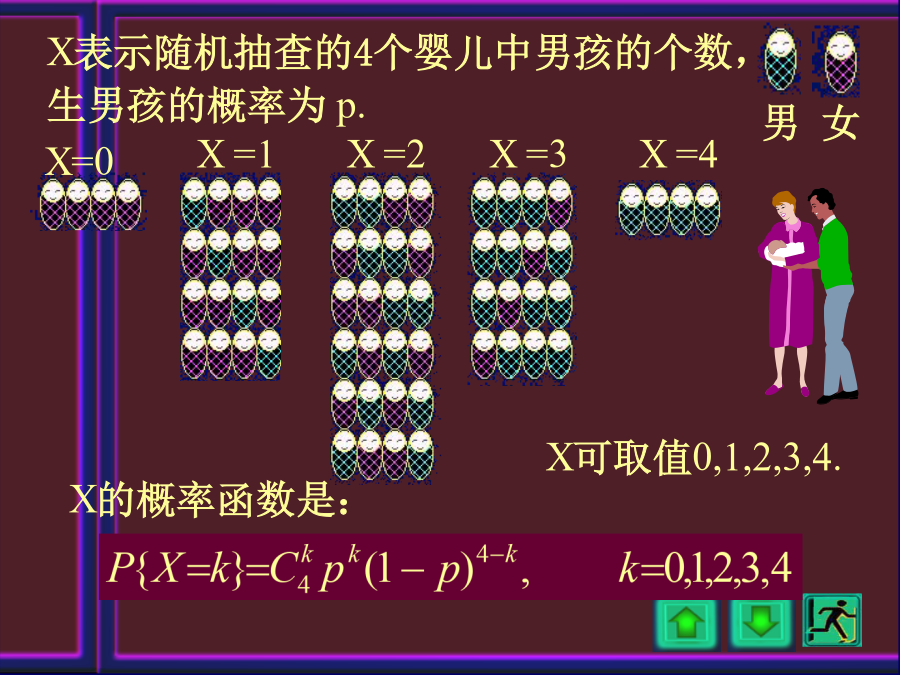
例1设生男孩的概率为p,生女孩的概率为
q=1-p，令X表示随机抽查出生的4个婴儿中“男孩”的个数.X的概率函数是：例2将一枚均匀骰子抛掷3次，
令X表示3次中出现“4”点的次数掷骰子：“掷出4点”，“未掷出4点”这样的n次独立重复试验称作n重贝努里试验，简称贝努里试验或贝努里概型.用X表示n重贝努里试验中事件A（成功）出现的次数，则例3已知100个产品中有5个次品，现从中
有放回地取3次，每次任取1个，求在所取的3个中恰有2个次品的概率.注：若将本例中的“有放回”改为”无放回”，那么各次试验条件就不同了，不是贝努里概型，此时，只能用古典概型求解.贝努里概型对试验结果没有等可能的要求，但有下述要求：例4某类灯泡使用时数在1000小时以上
的概率是0.2，求三个灯泡在使用1000
小时以后最多只有一个坏了的概率.对于固定n及p，当k增加时,概率P(X=k)先是随之增加直至达到最大值,随后单调减少.对于固定n及p，当k增加时,概率P(X=k)先是随之增加直至达到最大值,随后单调减少.想观看二项分布的图形随参数n,p的具体变化，请看演示二、二项分布的泊松近似证明见教材.n100,np10时近似效果就很好此例说明，当p不是很小，而是很大(接近于1)，可将问题略为转换一下，仍然可以应用泊松近似.例5为保证设备正常工作，需要配备适量的维修人员.设共有300台设备，每台的工作相互独立，发生故障的概率都是0.01.若在通常的情况下，一台设备的故障可由一人来处理.问至少应配备多少维修人员，才能保证当设备发生故障时不能及时维修的概率小于0.01?300台设备，独立工作，出故障概率都是0.01.一台设备故障一人来处理.
问至少配备多少维修人员，才能保证当设备发生故障时不能及时维修的概率小于0.01?300台设备，独立工作，出故障概率都是0.01.一台设备故障一人来处理.
问至少配备多少维修人员，才能保证当设备发生故障时不能及时维修的概率小于0.01?解：设X为300台设备同时发生故障的台数，即至少需配备8个维修人员.这一讲，我们介绍了二项分布.