高考数学总复习 5.1平面向量课件 文 大纲人教版 课件.ppt

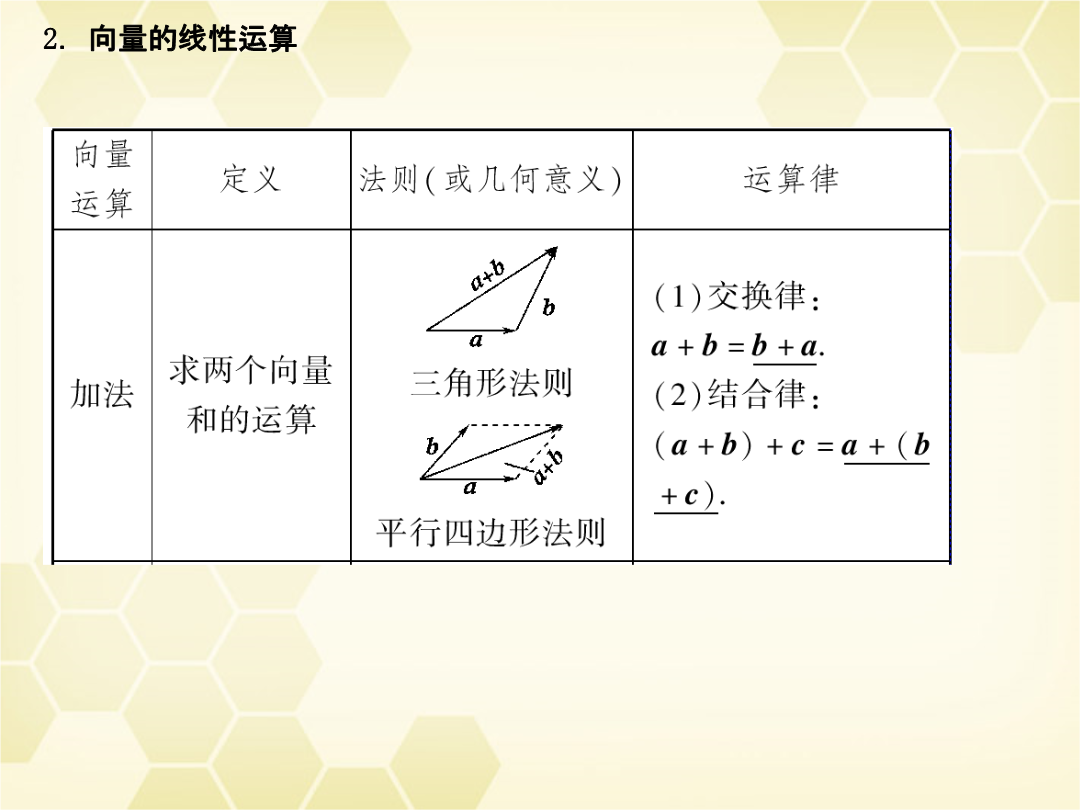
第五章平面向量平面向量的数量积第1课时平面向量的概念及运算(4)平行向量：方向相同或的向量；平行向量又叫向量．规定：0与任一向量．(5)相等向量：长度且方向的向量．(6)相反向量：长度且方向的向量．2．向量的线性运算3.两个重要定理(1)共线向量定理向量b与非零向量a共线的充要条件是有且仅有一个实数λ使得．(2)平面向量基本定理如果e1、e2是同一平面内的两个向量那么对于这一平面内的任一向量a有且仅有一对实数λ1、λ2使a＝.4．向量的坐标(1)平面向量的坐标表示在直角坐标系内分别取与x轴、y轴方向相同的两个单位向量i、j作为基底．由平面向量基本定理知该平面内的任一向量a可表示成a＝由于向量a与数对是一一对应的因此把叫做向量a的(直角)坐标记作a＝其中叫做a在x轴上的坐标叫做a在y轴上的坐标．(2)平面向量的坐标运算设a＝(x1y1)b＝(x2y2)．①a＋b＝②a－b＝③λa＝④若a∥b则.1．若a＝(32)b＝(0－1)则2b－a的坐标是()A．(3－4)B．(－34)C．(34)D．(－3－4)解析：∵2b－a＝2×(0－1)－(32)＝(0－2)－(32)＝(－3－4)故2b－a＝(－3－4)．答案：D解析：解析：4．已知a与b是两个不共线向量且向量a＋λb与－(b－3a)共线则λ＝________.解析：由已知得a＋λb＝－k(b－3a)解析：1．以平面内任意两个不共线的向量为一组基底该平面内的任意一个向量都可表示成这组基底的线性组合基底不同表示也不同．2．对于两个向量ab将它们用同一组基底表示我们可通过分析这两个表示式的关系来反映a与b的关系．3．利用已知向量表示未知向量实质就是利用平行四边形法则或三角形法则进行向量的加减运算或进行数乘运算．如图在平行四边形ABCD中MN分别为DCBC的中点[变式训练]1．向量的坐标运算主要是利用加、减、数乘运算法则进行若已知有向线段两端点的坐标则应先求出向量的坐标解题过程中要注意方程思想的运用．2．利用坐标运算求向量的基底表示一般先求出基底向量和被表示向量的坐标再用待定系数法求出系数．解析：(1)由已知得[变式训练]2.已知A(－24)B(3－1)C(－3－4)且a∥b的充要条件有两种表达形式：(1)a∥b(b≠0)a＝λb(λ∈R)；(2)设a＝(x1y1)b＝(x2y2)则a∥bx1y2－x2y1＝0.两种充要条件的表达形式不同第(1)种是用线性关系的形式表示的而且有前提条件b≠0.而第(2)种是用坐标形式表示的且没有b≠0的限制．已知a＝(10)b＝(21)(1)当k为何值时ka－b与a＋2b共线．解析：1．共线向量有以下四种情况：方向相同且模相等；方向相同且模不等；方向相反且模相等；方向相反且模不等．这样也就找到了共线向量与相等向量的关系即共线向量不一定是相等向量而相等向量一定是共线向量．2．共线定理的作用：用向量共线定理可以证明几何中的三点共线和直线平行问题．但是向量平行与直线平行是有区别的直线平行不包括重合的情况．要证明三点共线或直线平行都是先探索有关的向量满足向量等式b＝λa再结合条件或图形有无公共点证明几何位置．3．平面向量基本定理的应用平面向量基本定理是说同一平面内的任一向量都可以表示为两个不共线向量的线性组合这就为向量的坐标表示奠定了基础平面向量基本定理在向量运算及利用向量证明有关问题方面都有广泛的应用．通过对近三年高考试题的统计分析在整个命题过程中有以下的规律：1．考查热点：向量的几何表示和运算．2．考查形式：选择题、填空题和解答题均可能出现．3．考查角度：一是对向量的几何表示的考查、掌握这类问题首先要理解向量的加法、减法、实数与向量的积的几何表示．二是对向量共线的考查．首先正确理解两个向量共线的充要条件．三是对平面向量基本定理的考查．四是对平面向量的基本运算的考查．向量的基本运算包括几何运算和坐标运算．4．命题趋势：以平面图形为载体借助基向量表达交点位置或借助向量的坐标形式表达共线等问题．解析：如图所示∠1＝∠2解析：解析：解析：4．(2009·北京卷)已知向量a、b不共线c＝ka＋b(k∈R)d＝a－b.如果c∥d那么()A．k＝1且c与d同向B．k＝1且c与d反向C．k＝