SAS学习系列.-Logistic回归.pdf

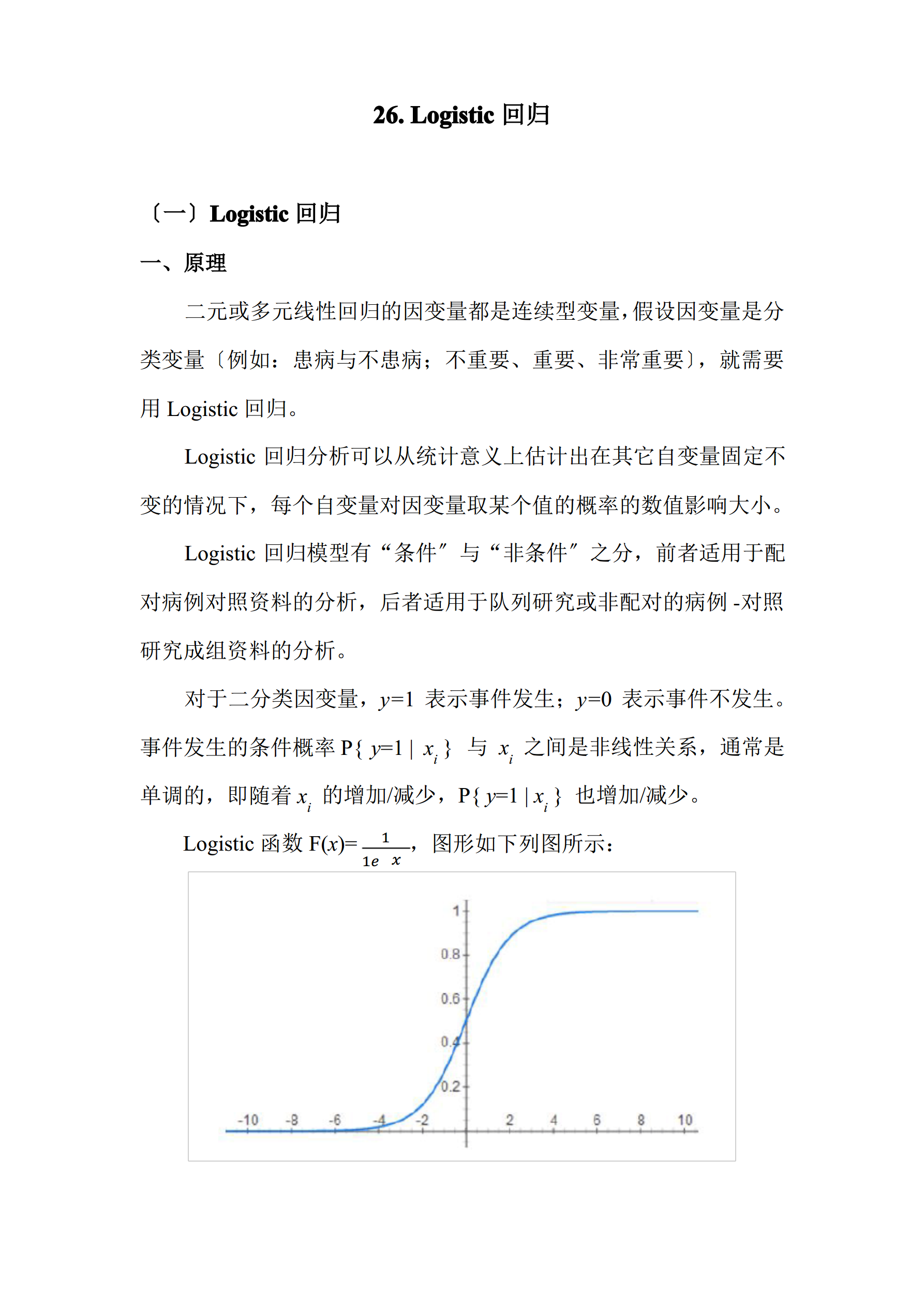
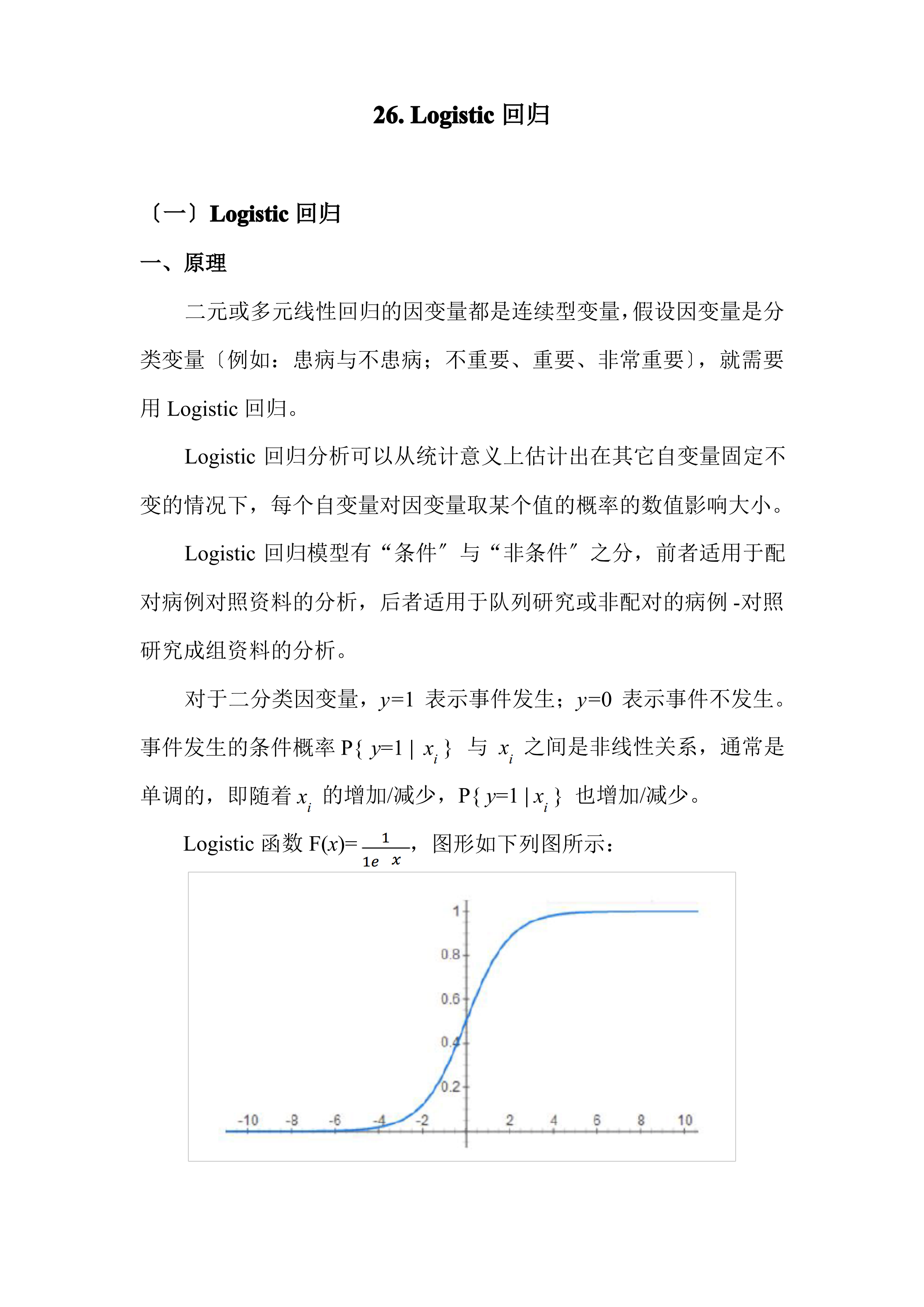
26.Logistic回归〔一〕Logistic回归一、原理二元或多元线性回归的因变量都是连续型变量，假设因变量是分类变量〔例如：患病与不患病；不重要、重要、非常重要〕，就需要用Logistic回归。Logistic回归分析可以从统计意义上估计出在其它自变量固定不变的情况下，每个自变量对因变量取某个值的概率的数值影响大小。Logistic回归模型有“条件〞与“非条件〞之分，前者适用于配对病例对照资料的分析，后者适用于队列研究或非配对的病例-对照研究成组资料的分析。对于二分类因变量，y=1表示事件发生；y=0表示事件不发生。事件发生的条件概率P{y=1|x}与x之间是非线性关系，通常是ii单调的，即随着x的增加/减少，P{y=1|x}也增加/减少。iiLogistic函数F(x)=1，图形如下列图所示：1𝑒𝑥该函数值域在(0,1)之间，x趋于-∞时，F(x)趋于0；x趋于+∞时，F(x)趋于1.正好适合描述概率P{y=1|x}.例如，某因素x导致患病与i否：x在某一水平段内变化时，对患病概率的影响较大；而在x较低或较高时对患病概率影响都不大。记事件发生的条件概率P{y=1|x}=p，那么iip=1=𝑒𝛼β𝑥𝑖i1𝑒(𝛼β𝑥𝑖)1𝑒𝛼β𝑥𝑖记事件不发生的条件概率为1-p=1i1𝑒𝛼β𝑥𝑖那么在条件x下，事件发生概率与事件不发生概率之比为i𝑝𝑖=𝑒𝛼β𝑥𝑖1𝑝𝑖称为事件的发生比，简记为odds.对odds取自然对数得到𝑝ln(𝑖)=𝛼β𝑥1𝑝𝑖𝑖上式左边〔对数发生比〕记为Logit(y),称为y的Logit变换。可见变换之后的Logit(y)就可以用线性回归，计算出回归系数α和β值。假设分类因变量y与多个自变量x有关，那么变换后Logit(y)可i由多元线性回归：plogit(p)ln()xxp111kk1或p(y1|x,,x)1k(xx)1e11kk二、回归参数的解释1.三个名词事件发生频数𝒑发生比〔odds〕==𝒌事件未发生频数𝟏𝒑𝒌例如，事件发生概率为0.6，不发生概率为0.4，那么发生比为1.5〔发生比>1，表示事件更可能发生〕。𝐨𝐝𝐝𝐬𝒑/(𝟏𝒑)𝒏/𝒏𝒏𝒏发生比率〔OR〕=𝟏=𝟏𝟏=𝟏𝟏𝟏𝟐=𝟏𝟏𝟐𝟐𝐨𝐝𝐝𝐬𝟐𝒑𝟐/(𝟏𝒑𝟐)𝒏𝟐𝟏/𝒏𝟐𝟐𝒏𝟏𝟐𝒏𝟐𝟏即主对角线乘积/副对角线乘积，也称为交叉积比率，优势比。例如，说明：大于1〔小于1〕的发生比率，说明事件发生的可能性会提高〔降低〕，或自变量对事件概率有正〔负〕的作用；发生比率为1表示变量对事件概率无作用。𝒑𝒏/(𝒏𝒏)相对风险〔RR〕=𝟏=𝟏𝟏𝟏𝟏𝟏𝟐𝒑𝟐𝒏𝟐𝟏/(𝒏𝟐𝟏𝒏𝟐𝟐)用来进行两组概率之间的比拟。当p=p时，相对风险为1，说明两12组在事件发生方面没有差异。2.连续型自变量回归参数的解释截距α：基准发生比的对数，即当Logistic回归模型中没有任何自变量时〔除常量外，所有自变量都取0值〕所产生的发生比。由于理解发生比，比理解对数发生比更容易，故将Logistic回归模型改写为：𝑝odds==𝑒𝛼𝛽1𝑥1⋯𝛽𝑘𝑥𝑘=𝑒𝛼×𝑒𝛽1𝑥1×⋯×𝑒𝛽𝑘𝑥𝑘1𝑝假设β>0〔β<0〕，那么𝑒𝛽>1〔𝑒𝛽<1〕,即x每增加一个单位值时kk𝑘𝑘k发生比会相应增加〔减少〕；假设β=0，那么𝑒𝛽=1,那么x不管怎样k𝑘k变化发生比都不会变化。𝑒𝛽反映了自变量x增加一个单位时发生比所变化的倍数，即𝑘k(x+1)时的发生比与原发生比【(x)时】之比。自变量x每变化一个单kkk位，发生比率的变化率为(𝑒𝛽𝑘−1)×100%注：由于β是自变量x的偏系数估计，故𝛽称为调整发生比率kk𝑒𝑘〔AOR〕的估计。实际中，往往更关心的不是自变量变化1个单位，而是变化一段水平b-a个单位，例如年龄每增加5岁，此时调整发生比率为AOR=𝑒(b−a)𝛽𝑘3.二分类自变量回归参数的解释二分类变量，例如性别，取值可以用0或1编码，也称为标志变量或虚拟变量。假设x为取值0或1的二分类变量，那么有kpln(i)x1x111k1pkipln(i)x0x011k1pki两式作差得ppln(i)ln(i)ln(odds)kx1x0x1vsx01pk1pkkkii可见β就是在控制其它变量条件下，x=1与x=0的对数发生比的差；kkk也即是发生比率的对数，即调整发生比率的估计可表示为AOR=𝑒𝛽𝑘=(odds)x1vsx0kk𝑝/(1𝑝)𝑝1𝑝𝑝注意，发生比率是11=(1)(2)，而不是两者概率比1𝑝2/(1𝑝2)𝑝21𝑝1𝑝24.多分类变量的处理与回归参数的解释当分类自变量多于两个类别时，需要建立一组虚拟变量来代表类型的归属性质。假设一个分类变量包括m个类别，那么可以产生m个相应的虚拟变量，但建模需要的虚拟变量的数目为m-1.