山东省泰安中考数学一轮复习《第27讲：概率》课件.pptx

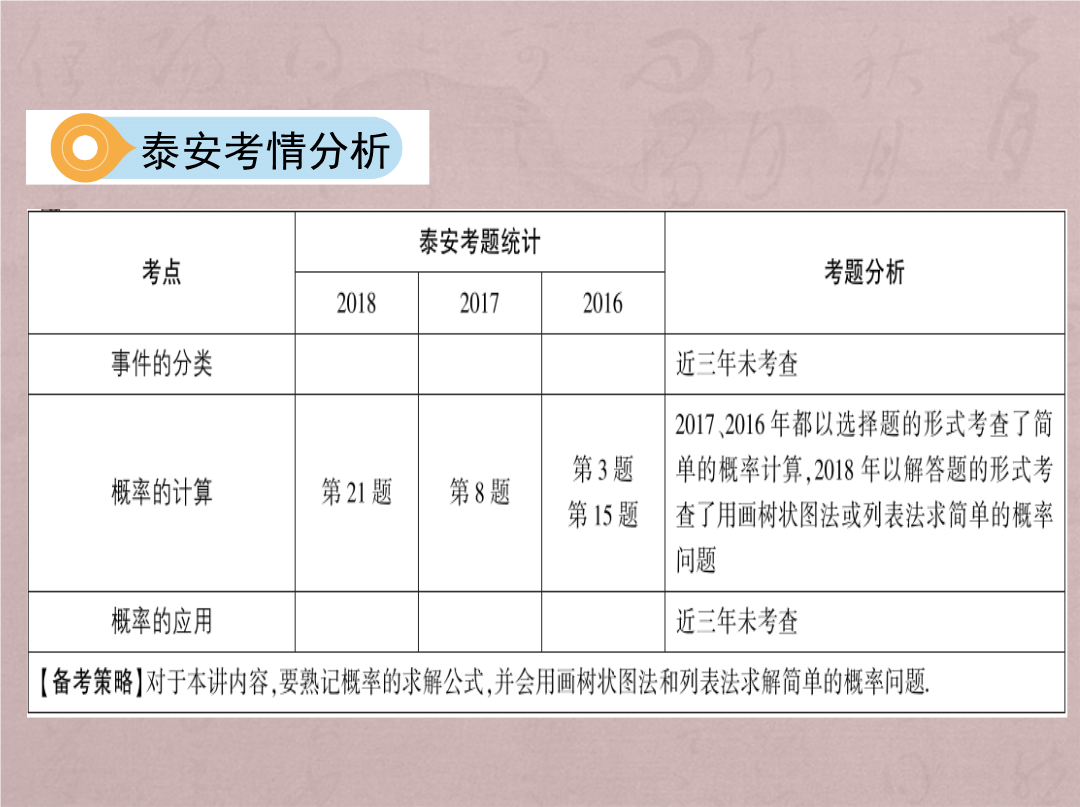
第27讲概率泰安考情分析泰安考情分析基础知识过关事件类型知识点二概率的计算1.一个事件发生的可能性的大小,可以用一个数来表示,我们把这个数叫做这个事件发生的④概率.2.一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中m种结果,那么事件A发生的概率⑤P(A)= .3.列表法和画树状图法求概率:当事件中包含两个因素时,可以用列表法列举出所有可能的结果,再根据概率公式计算;当事件中涉及两个或两个以上的因素时,通常采用画树状图列举出所有的结果,再根据概率公式计算.知识点三用频率估计概率1.当试验次数足够大时,事件A发生的频率 越来越稳定于某个常数,这个常数就可以当作概率的估计值.2.一般地,在大量重复试验中,如果事件A发生的频率 稳定在某个常数p附近,那么事件A发生的概率P(A)= .3.频率与概率的区别和联系:频率和概率是两个不同的概念,事件发生的概率是一个确定的值(理论值),而频率是不确定的值(试验值).当试验次数较少时,频率的大小摇摆不定,当试验的次数较大时,频率的大小波动变小,逐渐稳定在概率附近.温馨提示概率的求法关键是要找准两点:(1)全部情况的总数;(2)符合条件的情况数.二者的比值就是其发生的概率.知识点四概率的应用概率的应用主要是用来评判某项活动是否合理,游戏是否公平.此类题目通常先计算事件发生的概率,然后利用概率的大小作出评判并解决问题.(1)评判游戏是否公平的原则:游戏双方获胜的概率如果相等,说明游戏是公平的,否则说明游戏不公平.(2)游戏规则的修改:对于任何一个游戏,修改它规则的方法不是唯一的,但最基本的是通过计算,使概率朝着相等的方向修改.泰安考点聚焦考点一判断事件的类型例1(2018淄博)下列语句描述的事件中,是随机事件的为(D)A.水能载舟,亦能覆舟B.只手遮天,偷天换日C.瓜熟蒂落,水到渠成D.心想事成,万事如意解析A.水能载舟,亦能覆舟,是必然事件,故此选项错误;B.只手遮天,偷天换日,是不可能事件,故此选项错误;C.瓜熟蒂落,水到渠成,是必然事件,故此选项错误;D.心想事成,万事如意,是随机事件,故此选项正确.故选D.变式1-1下列说法属于不可能事件的是 (D)A.四边形的内角和为360°B.对角线相等的菱形是正方形C.内错角相等D.存在实数x满足x2+1=0解析四边形的内角和为360°是必然事件;对角线相等的菱形是正方形是必然事件;内错角相等是随机事件;存在实数x满足x2+1=0是不可能事件,故选D.考点二简单事件的概率例2(2018聊城)某十字路口设有交通信号灯,东西方向信号灯的开启规律如下:红灯开启30秒后关闭,紧接着黄灯开启3秒后关闭,再紧接着绿灯开启42秒后关闭,按此规律循环下去.如果不考虑其他因素,当一辆汽车沿东西方向随机地行驶到该路口时,遇到红灯的概率是 .解析P= = .变式2-1(2016泰安)下列图形: 从中任取一个图,是中心对称图形的概率是 (C)A. B. C. D.1解析第1、3、4个图形是中心对称图形,∴任取一个图,是中心对称图形的概率是 .故选C.方法技巧在一次试验中,求出总的结果数n和该事件包含的结果数m,然后利用公式P= 计算该事件发生的概率.考点三用列表法或画树状图法求概率中考解题指导用列表法或画树状图法求概率是泰安中考必考知识点,题目较为简单.列表法适合于两步完成的事件,画树状图法适合两步或两步以上完成的事件.例3(2017泰安)袋内装有标号分别为1、2、3、4的4个球,从袋内随机取出一个小球,让其标号为一个两位数的十位数字,放回搅匀后,再随机取出一个小球,让其标号为这个两位数的个位数字,则组成的两位数是3的倍数的概率为 (B)A. B. C. D. 解析列表如下:变式3-1(2016泰安)在-2,-1,0,1,2这五个数中任取两数m,n,则抛物线y=(x-m)2+n的顶点在坐标轴上的概率为 (A)A. B. C. D. 解析画树状图得: ∴-2,-1,0,1,2这五个数中任取两数m,n,一共有20种可能,其中符合条件的有8种可能,∴顶点在坐标轴上的概率为 = .变式3-2(2018滨州)若从-1,1,2这三个数中,任取两个数分别作为点M的横、纵坐标,则点M在第二象限的概率是 .解析列表如下:由表可知,共有6种等可能结果,其中点M在第二象限的结果有2种,所以点M在第二象限的概率是 = ,故答案为 .方法技巧注意列表法或画树状图法必须要不重复不遗漏地列出所有可能的结果,再利用概率公式求得答案.考点四用频率估计概率中考解题指导当试验次数很多或试验样本容量足够大时,该事件发生的频率与相应的概率会非常接近.此时,我们可以用事件发生的频率来估计这一事件发生的概率.例4在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他