条件概率、全概公式、贝叶斯公式市公开课一等奖省赛课获奖PPT课件.pptx

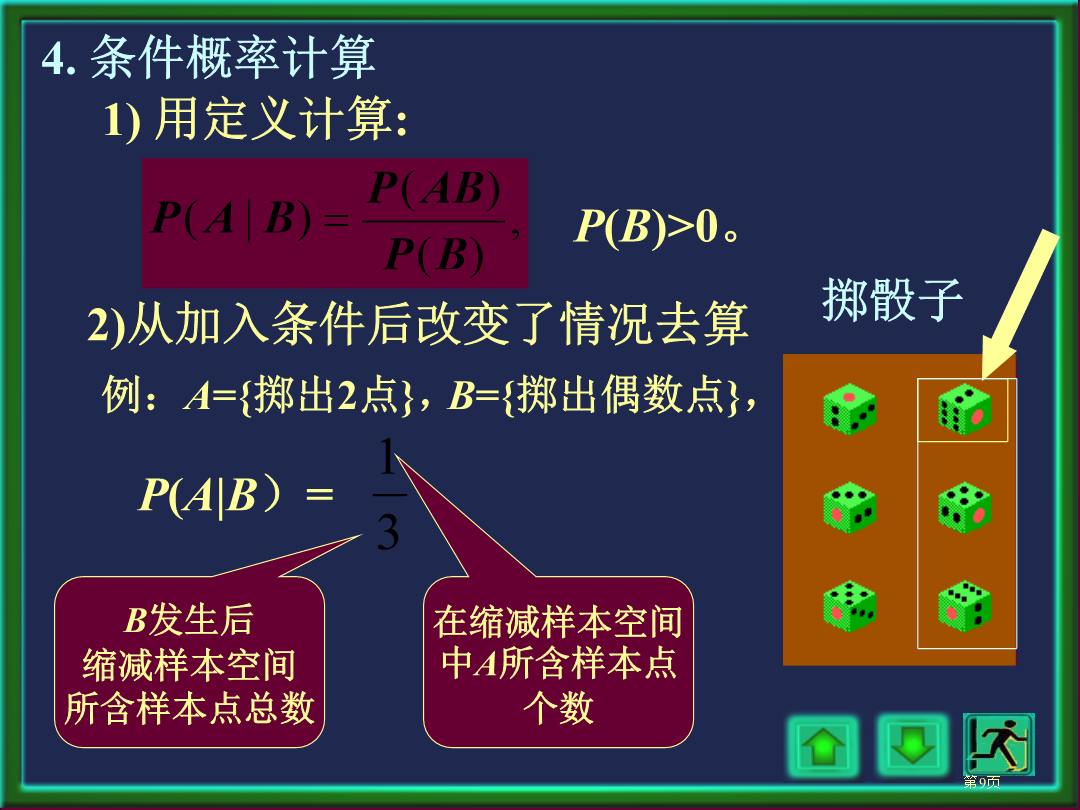
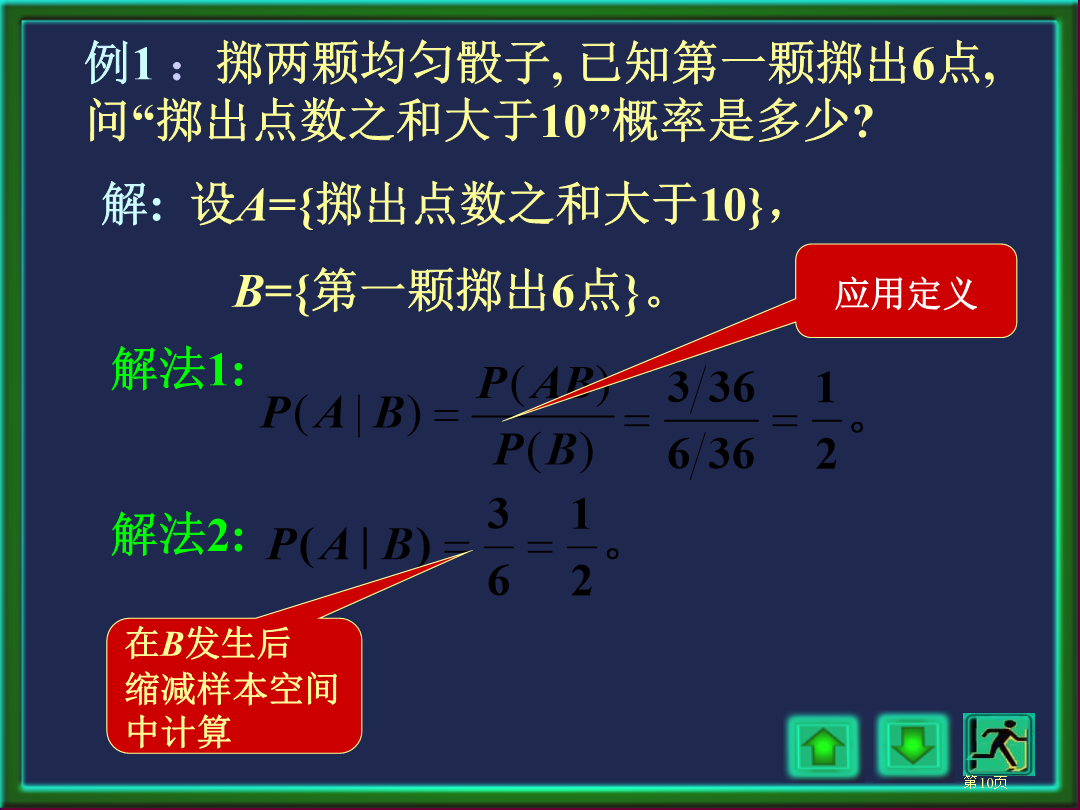
P(A)=1/6，P(A)=3/10，P(A)=3/10，若事件B已发生,则为使A也发生,试验结果必须是既在B中又在A中样本点,即此点必属于AB。因为我们已经知道B已发生,故B就变成了新样本空间,于是就有(1)。3.条件概率性质比如：对任意事件A1和A2,有P(A1∪A2|B)=P(A1|B)+P(A2|B)-P(A1A2|B)等。例1：掷两颗均匀骰子,已知第一颗掷出6点,问“掷出点数之和大于10”概率是多少?例2:设某种动物由出生算起活到20年以上概率为0.8，活到25年以上概率为0.4。问现年20岁这种动物，它能活到25岁以上概率是多少？条件概率P(A|B)与P(A)区分由条件概率定义：例3:甲、乙两厂共同生产1000个零件，其中300件是乙厂生产。而在这300个零件中，有189个是标准件，现从这1000个零件中任取一个，问这个零件是乙厂生产标准件概率是多少？所求为P(AB)。当P(A1A2…An-1)>0时，有P(A1A2…An）=P(A1)P(A2|A1)…P(An|A1A2…An-1)。解:解:一场精彩足球赛将要举行,但5个球迷只搞到一张球票，但大家都想去。没方法，只好用抽签方法来确定球票归属。到底谁说对呢？让我们用概率论知识来计算一下,每个人抽到“入场券”概率到底有多大?我们用Ai表示“第i个人抽到入场券”，i＝1,2,3,4,5。因为若第2个人抽到入场券时，第1个人必定没抽到。这就是相关抽签次序问题正确解答———将此例中所用方法推广到普通情形，就得到在概率计算中惯用全概率公式。设A1,A2,…,An是两两互斥事件，且P(Ai)>0，i=1,2,…,n,另有一事件B,它总是与A1,A2,…,An之一同时发生，则称满足上述条件A1,A2,…,An为完备事件组。在较复杂情况下，直接计算P(B)不轻易,但总能够适当地结构一组两两互斥Ai，使B伴伴随某个Ai出现而出现，且每个轻易计算。可用全部之和计算P(B)。某一事件B发生有各种可能原因Ai(i=1,2,…,n)，假如B是由原因Ai所引发，则B发生概率是由此能够形象地把全概率公式看成是“由原因推结果”，每个原因对结果发生有一定“作用”，即结果发生可能性与各种原因“作用”大小相关。全概率公式表示了因果之间关系。例7:甲、乙、丙三人同时对飞机进行射击,三人击中概率分别为0.4、0.5、0.7。飞机被一人击中而击落概率为0.2,被两人击中而击落概率为0.6,若三人都击中,飞机必定被击落,求飞机被击落概率。可求得于是，P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+P(A3)P(B|A3)该球取自哪号箱可能性大些?接下来我们介绍处理这类问题有三个箱子，编号分别为1,2,3，1号箱装有1个红球4个白球，2号箱装有2红球3白球，3号箱装有3红球.。某人从三箱中任取一箱，从中任意摸出一球，发觉是红球,求该球是取自1号箱概率。某人从任一箱中任意摸出一球，发觉是红球，求该球是取自1号箱概率。该公式于1763年由贝叶斯(Bayes)给出。它是在观察到事件B已发生条件下，寻找造成B发生每个原因概率。贝叶斯公式在实际中有很多应用，它能够帮助人们确定某结果（事件B）发生最可能原因.例8:某一地域患有癌症人占0.005，患者对一个试验反应是阳性概率为0.95，正常人对这种试验反应是阳性概率为0.04，现抽查了一个人，试验反应是阳性，问此人是癌症患者概率有多大?现在来分析一下结果意义假如不做试验,抽查一人,他是患者概率P(C)=0.005。2.检出阳性是否一定患有癌症?8支步枪中有5支已校准过,3支未校准。一名射手用校准过枪射击时,中靶概率为0.8;用未校准枪射击时,中靶概率为0.3。现从8支枪中任取一支用于射击,结果中靶。求:所用枪是校准过概率。解:由贝叶斯公式，得小结