
15定积分省公开课一等奖全国示范课微课金奖PPT课件.pptx

胜利****实阿





亲,该文档总共35页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

15定积分省公开课一等奖全国示范课微课金奖PPT课件.pptx
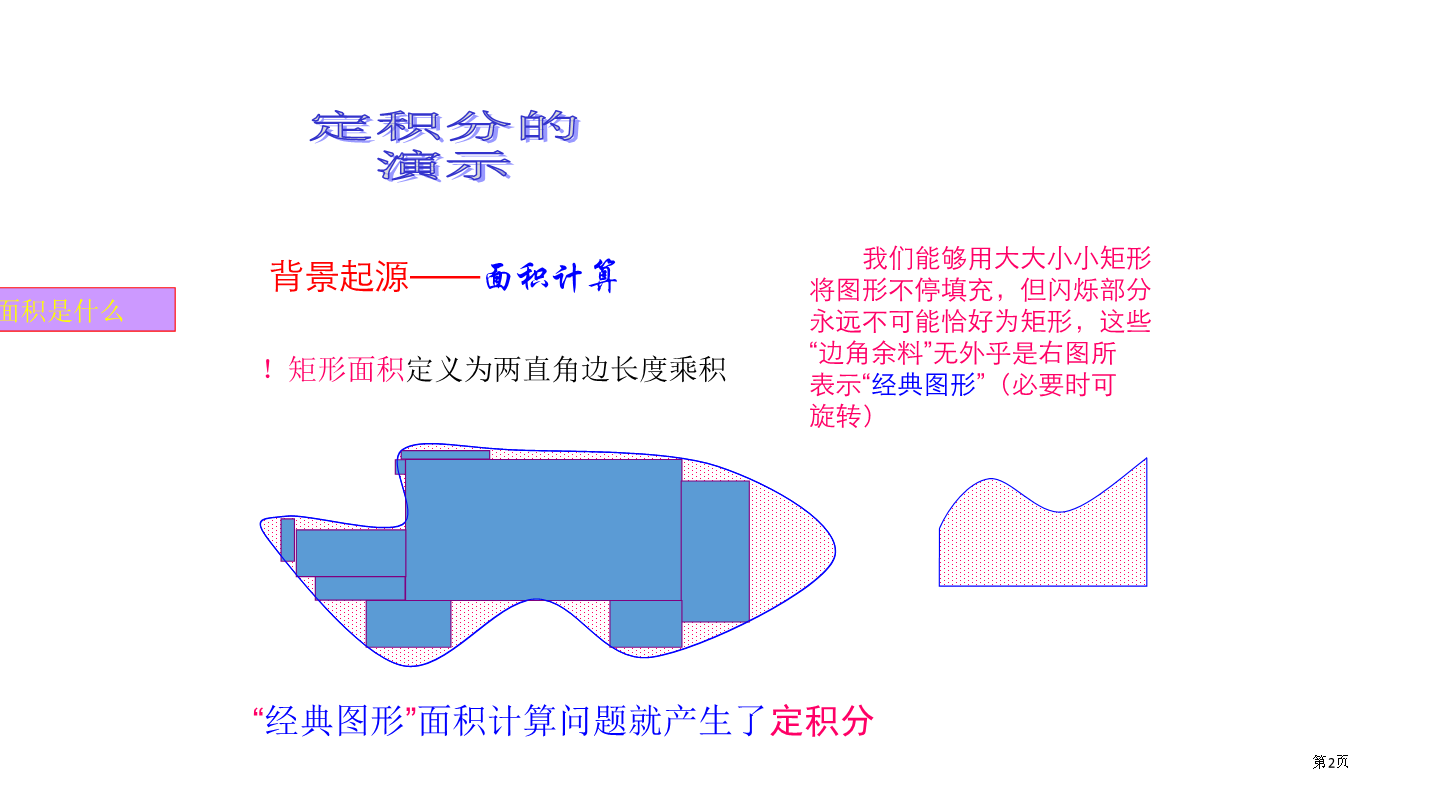
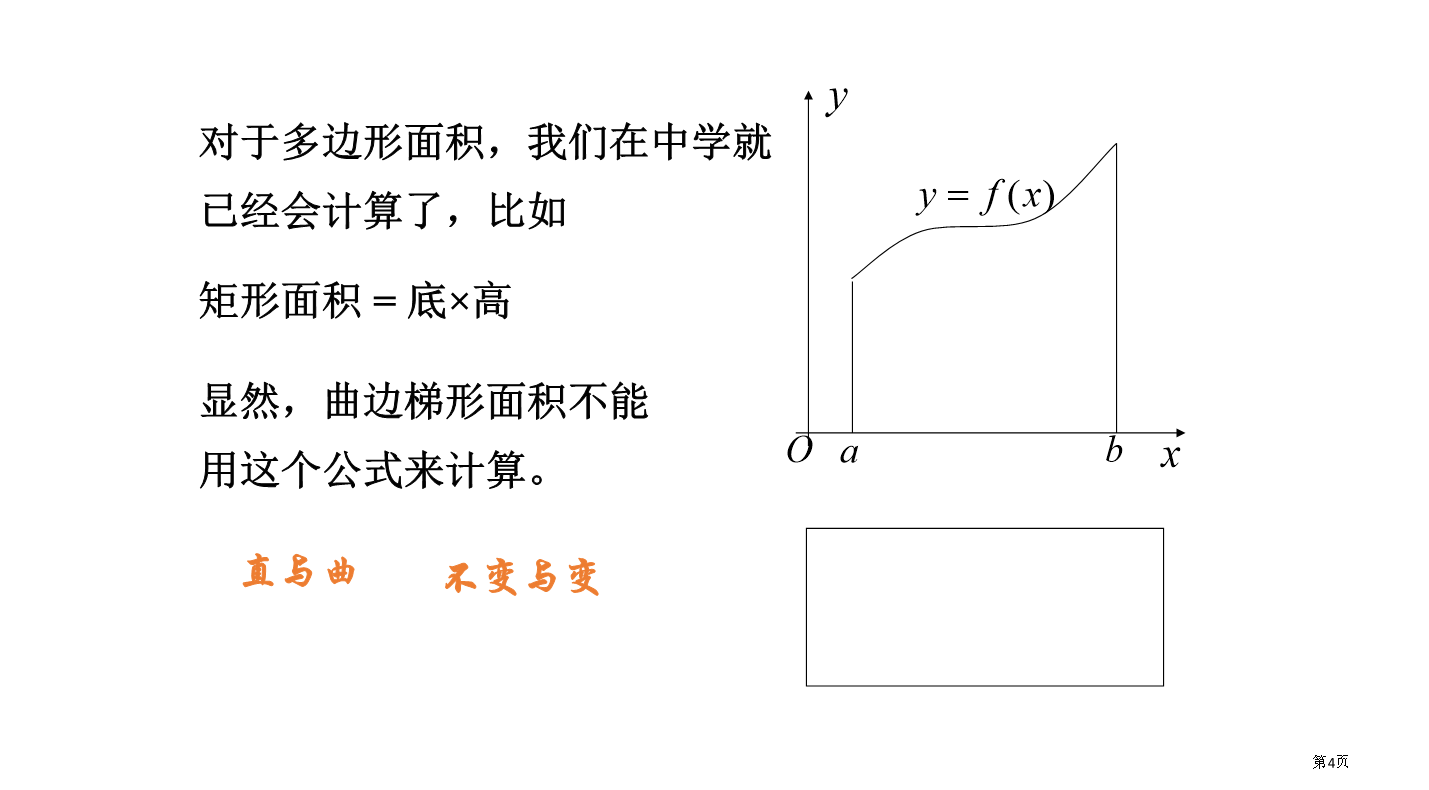
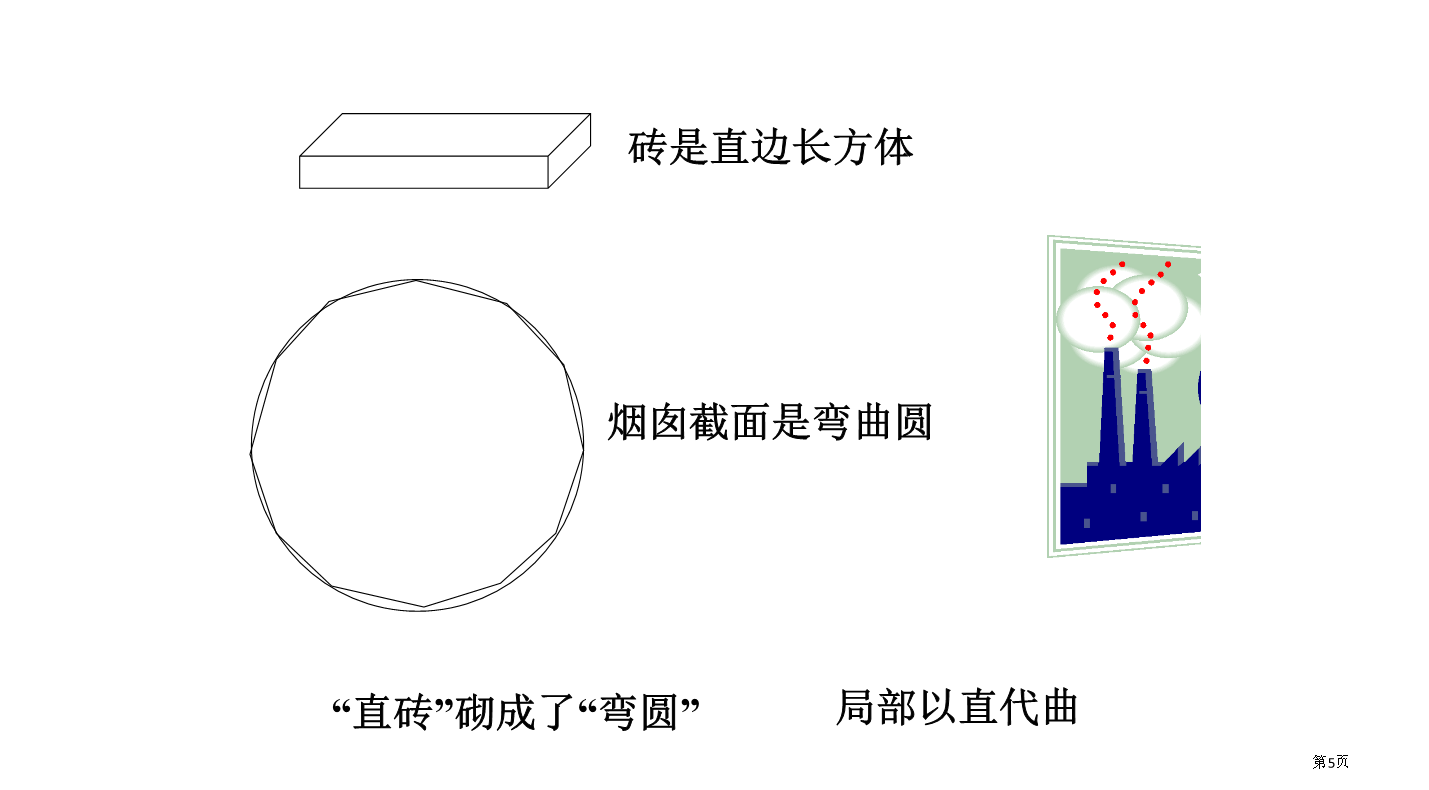
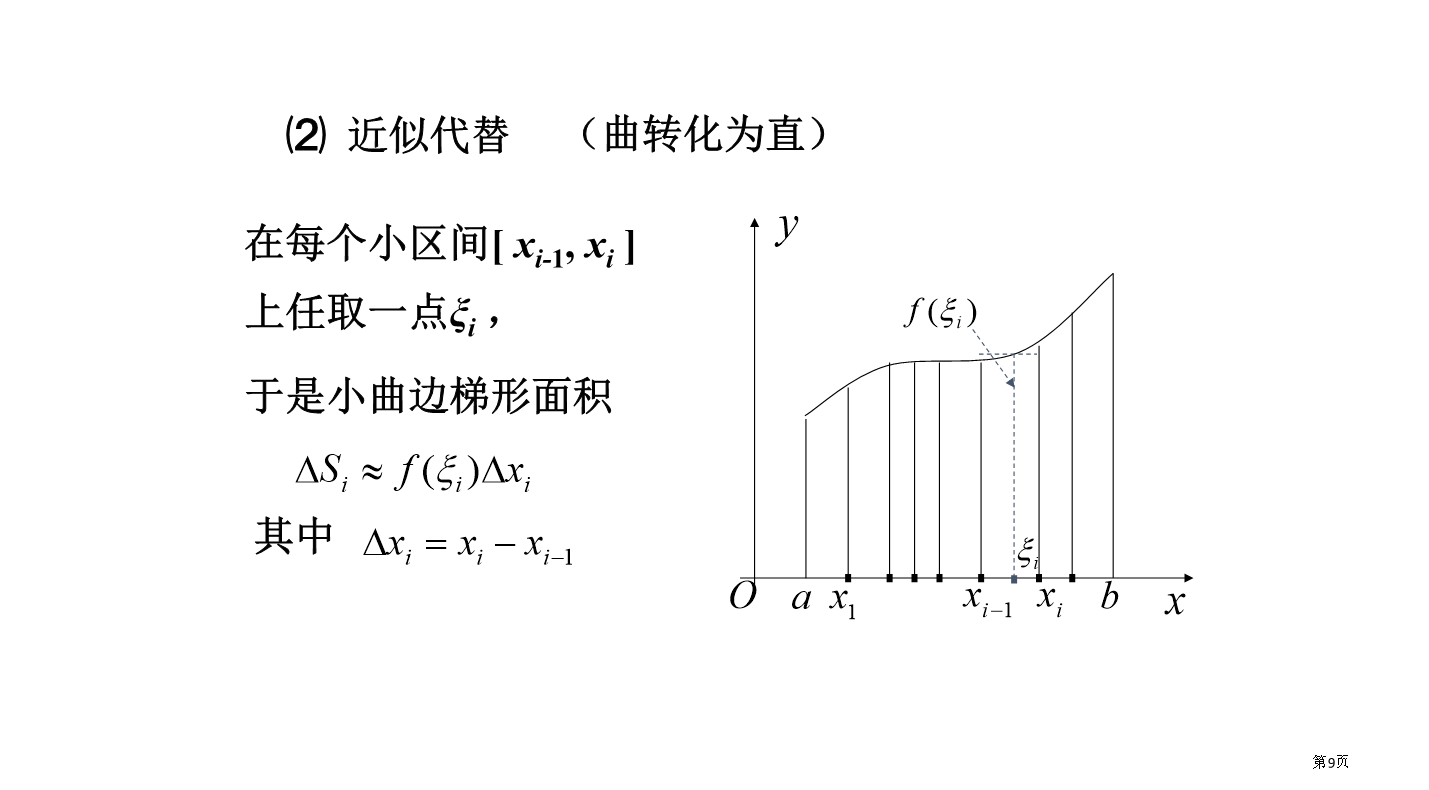
一、问题提出定积分的演示一、问题提出对于多边形面积,我们在中学就已经会计算了,比如矩形面积=底×高⑶求和⑷取极限求曲边梯形面积表达了曲转化为直、直转化为曲辩证思想。这个计算过程,就是一个先微分后积分过程。也就是说,把曲边梯形分割成许多小曲边梯形,在每个小曲边梯形中,把曲边看成直边,用这些小“矩形”面积和近似地表示原来大曲边梯形面积,从而实现了局部曲转化为局部直,即“以直代曲”。然后,再把分割无限加细,经过取极限,就使小矩形面积和,转化为原来大曲边梯形面积。这么局部直又反过来转化为整体曲。这种曲转化为直,直

数值积分省公开课一等奖全国示范课微课金奖PPT课件.pptx
7.3Romberg积分我们希望找到一个简便方法,用近似公式F(h)组合,得到误差阶较高近似公式,使(2)此时,迫近F*误差为O(h2)类似地,用组合产生迫近F*误差为O(h3)近似公式等.下面我们给出一个详细组合方法.把(1)式改写为(3)用h/2代替(3)式中h,得(4)用2乘(4)式再减去(3)式,消去含h项,得(5)令,且记那么(5)式可写为(6)这里,迫近误差为再用h/2代替h,使(6)式变为(7)用4乘(7)式减去(6)式,消去含项,得(8)一样记(8)式能够写为(9)这里迫近误差为还是用h/

141曲边梯形的面积与定积分省公开课一等奖全国示范课微课金奖PPT课件.pptx
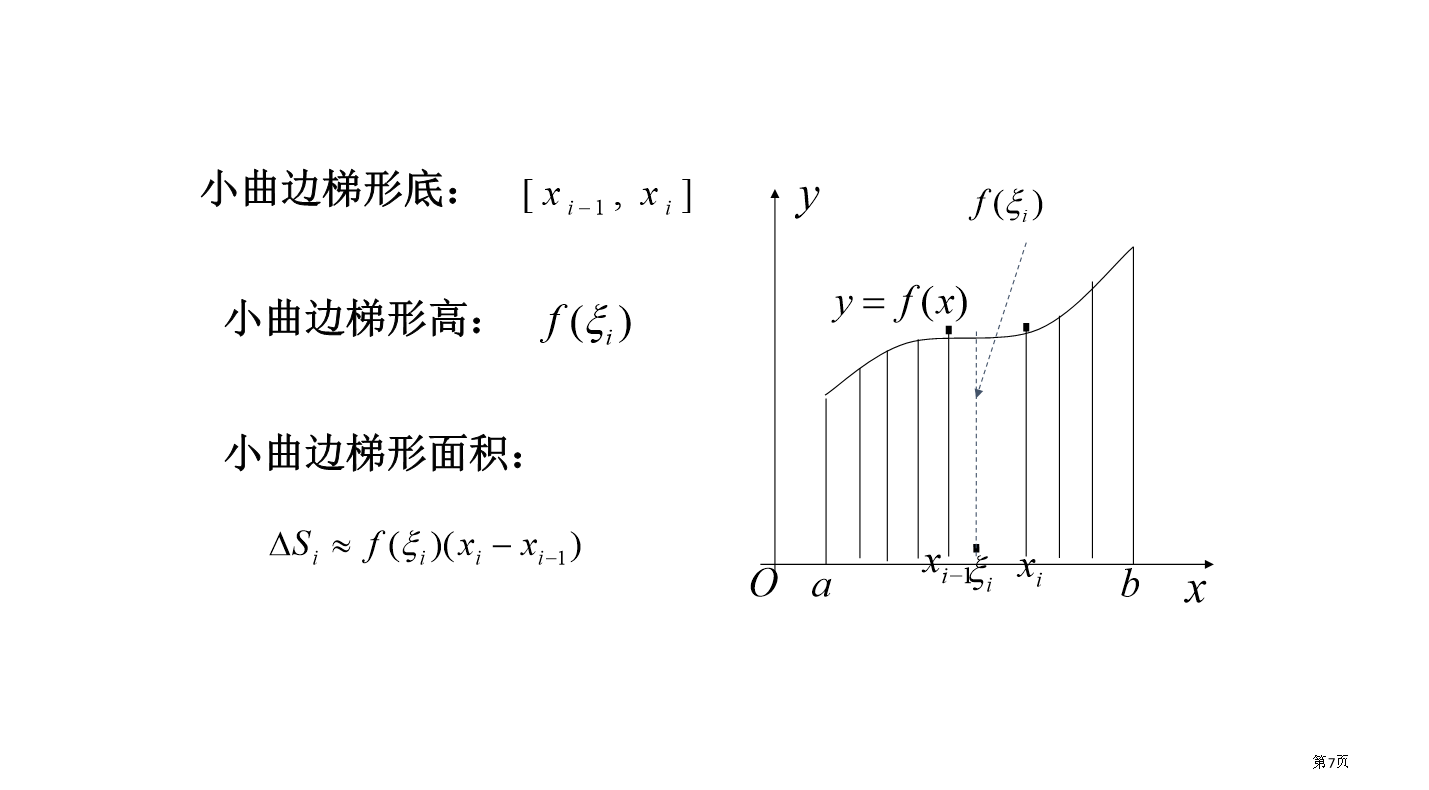
曲边梯形面积与定积分微积分在几何上有两个基本问题曲边梯形的面积曲边梯形面积当分点非常多(n非常大)时,能够认为f(x)在小区间上几乎没有改变(或改变非常小),从而能够取小区间内任意一点xi对应函数值f(xi)作为小矩形一边长,于是f(xi)△x来近似表示小曲边梯形面积观察以下演示,注意当分割加细时,矩形面积和与曲边梯形面积关系。观察以下演示,注意当分割加细时,矩形面积和与曲边梯形面积关系。观察以下演示,注意当分割加细时,矩形面积和与曲边梯形面积关系。观察以下演示,注意当分割加细时,矩形面积和与曲边梯形面积

欧拉积分省公开课一等奖全国示范课微课金奖PPT课件.pptx
§3欧拉积分含参量积分:Γ函数Β函数Γ函数与Β函数之间关系1.积分区间为无穷;其中1.Γ函数在定义域s>0内连续且可导4.延拓三、函数总而言之,2.性质(2)(4)二、Β函数1.B(p,q)在定义域p>0,q>0内连续4.B(p,q)其它形式三、Γ函数与Β函数之间关系例例

数值微积分省公开课一等奖全国示范课微课金奖PPT课件.pptx
4.5高斯求积公式4.5.1普通理论为含有普通性,研究带权积分依据定义要使(5.1)含有次代数精度,只要对例5因为深入整理得这么,形如(5.3)高斯公式是定理5是高斯点,因为求积公式(5.1)是插值型,它对于是准确,可见求积公式(5.1)对一切次数不超出多项式均精确成立.所以,为高斯点.下面讨论高斯求积公式(5.1)余项.两端乘,并由到积分,则得定理6由本定理及定理2,则得4.5.2高斯-勒让德求积公式令它对准确成立,即可定出令它对都准确成立,有20由(5.8)式,得可将化为,例64.5.3高斯-切比雪夫
