预览加载中，请您耐心等待几秒...

141曲边梯形的面积与定积分省公开课一等奖全国示范课微课金奖PPT课件.pptx

预览
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10

亲，该文档总共37页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示 文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

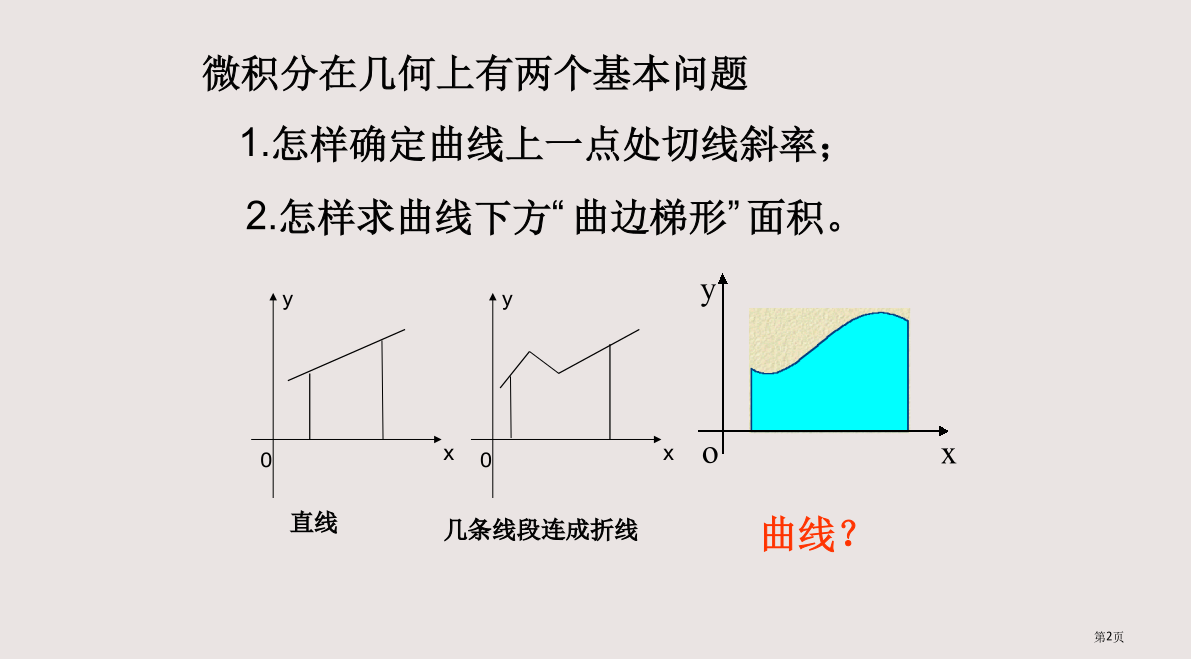
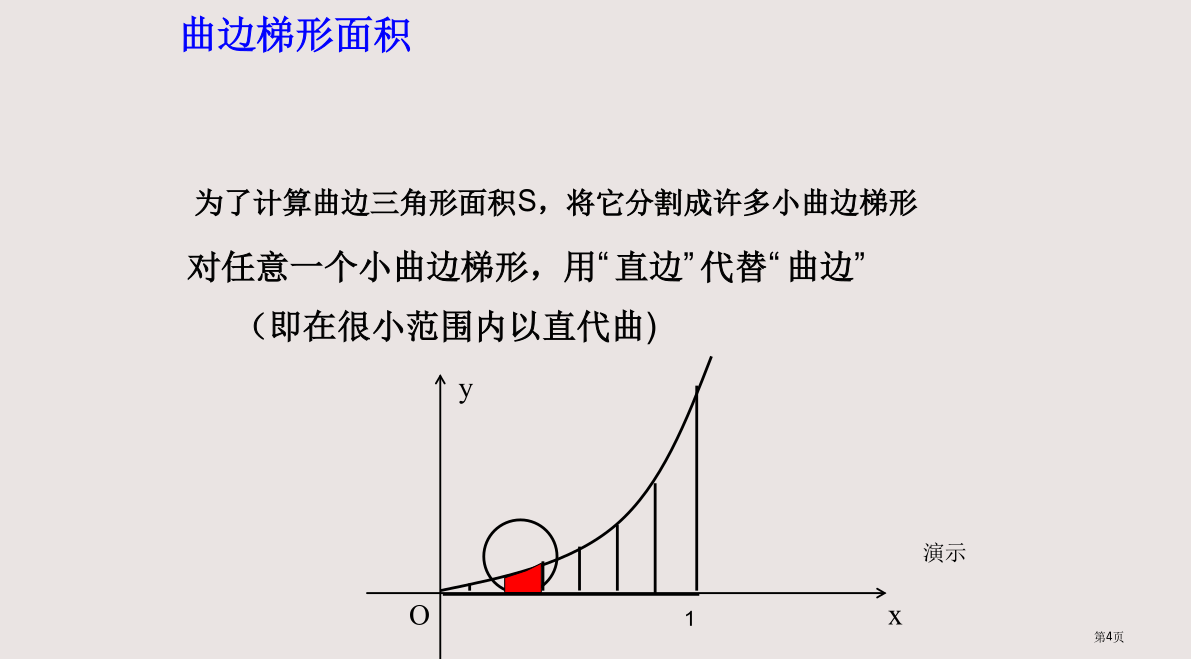
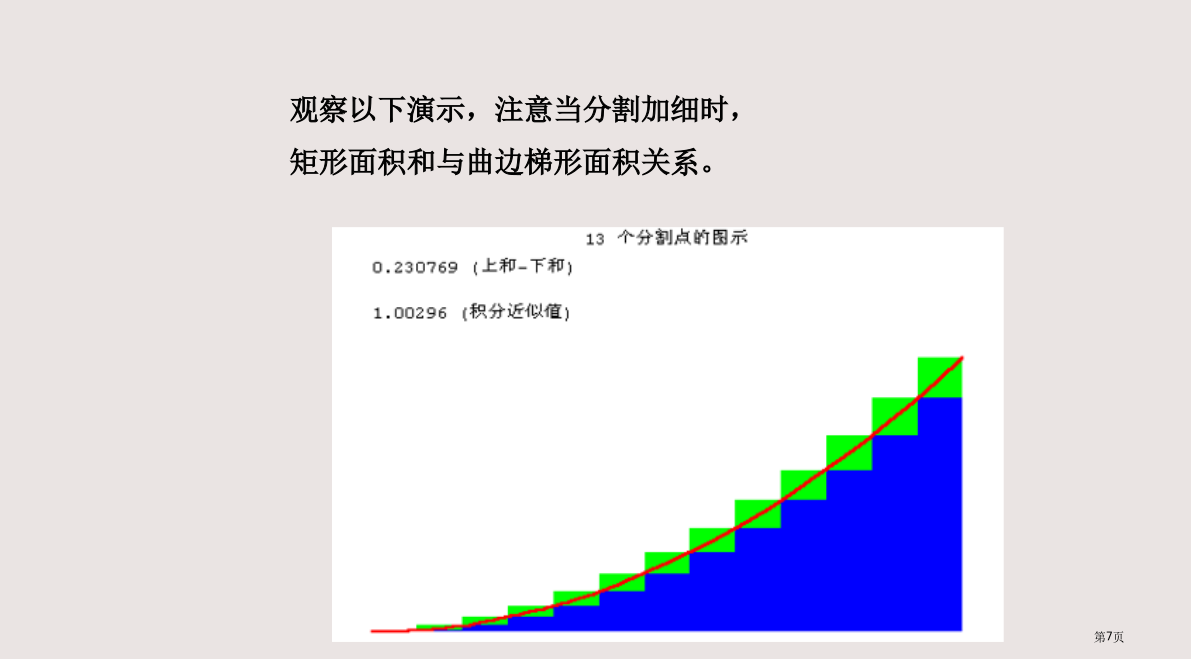
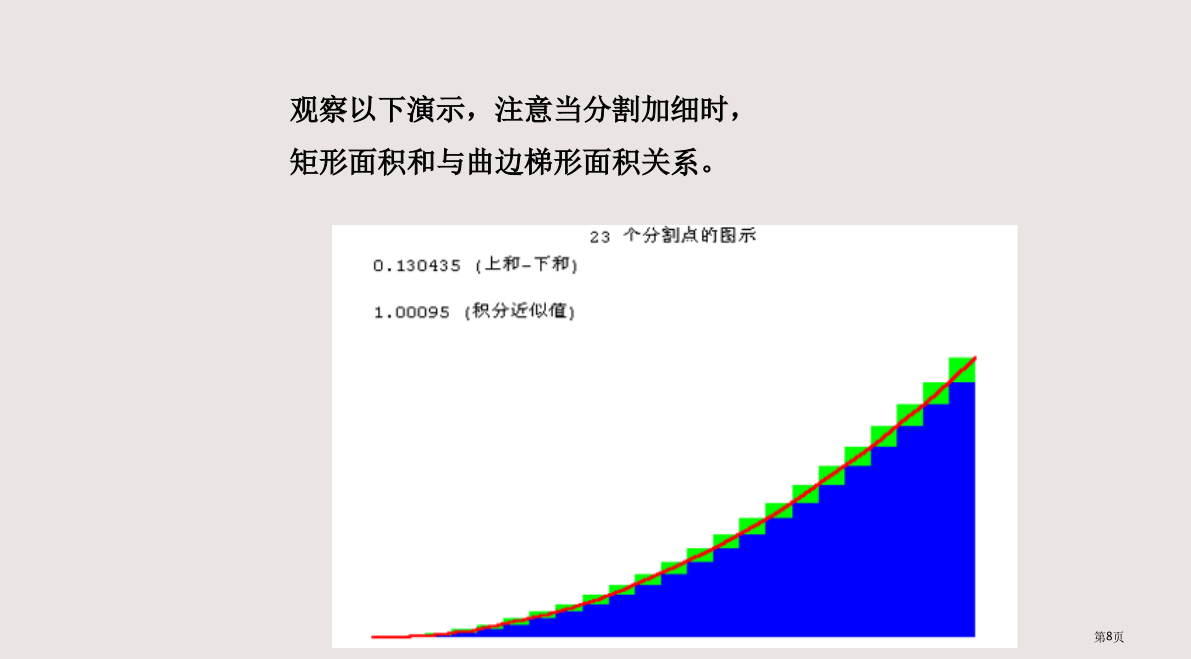
曲边梯形面积与定积分微积分在几何上有两个基本问题曲边梯形的面积曲边梯形面积当分点非常多（n非常大）时，能够认为f(x)在小区间上几乎没有改变（或改变非常小），从而能够取小区间内任意一点xi对应函数值f(xi)作为小矩形一边长，于是f(xi)△x来近似表示小曲边梯形面积观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。观察以下演示，注意当分割加细时， 矩形面积和与曲边梯形面积关系。分割越细，面积近似值就越准确。当分割无限变细时，这个近似值就无限迫近所求曲边梯形面积S。（1）分割（2）近似代替（4）取极限y=f(x)分割弹簧在拉伸过程中，力与伸长量成正比，即力F(x)=kx（k是常数，x是伸长量），求弹簧从平衡位置拉长b所作功。当n很大时，在分段[xi，xi+1]所用力约为kxi，所做功△W≈kxi·△x=于是得到弹簧从平衡位置拉长b所做功为1.曲边三角形或梯形面积 S=定积分的概念普通函数定积分定义定积分性质: