
初中数学教师学科知识竞赛.doc

胜利****实阿





在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

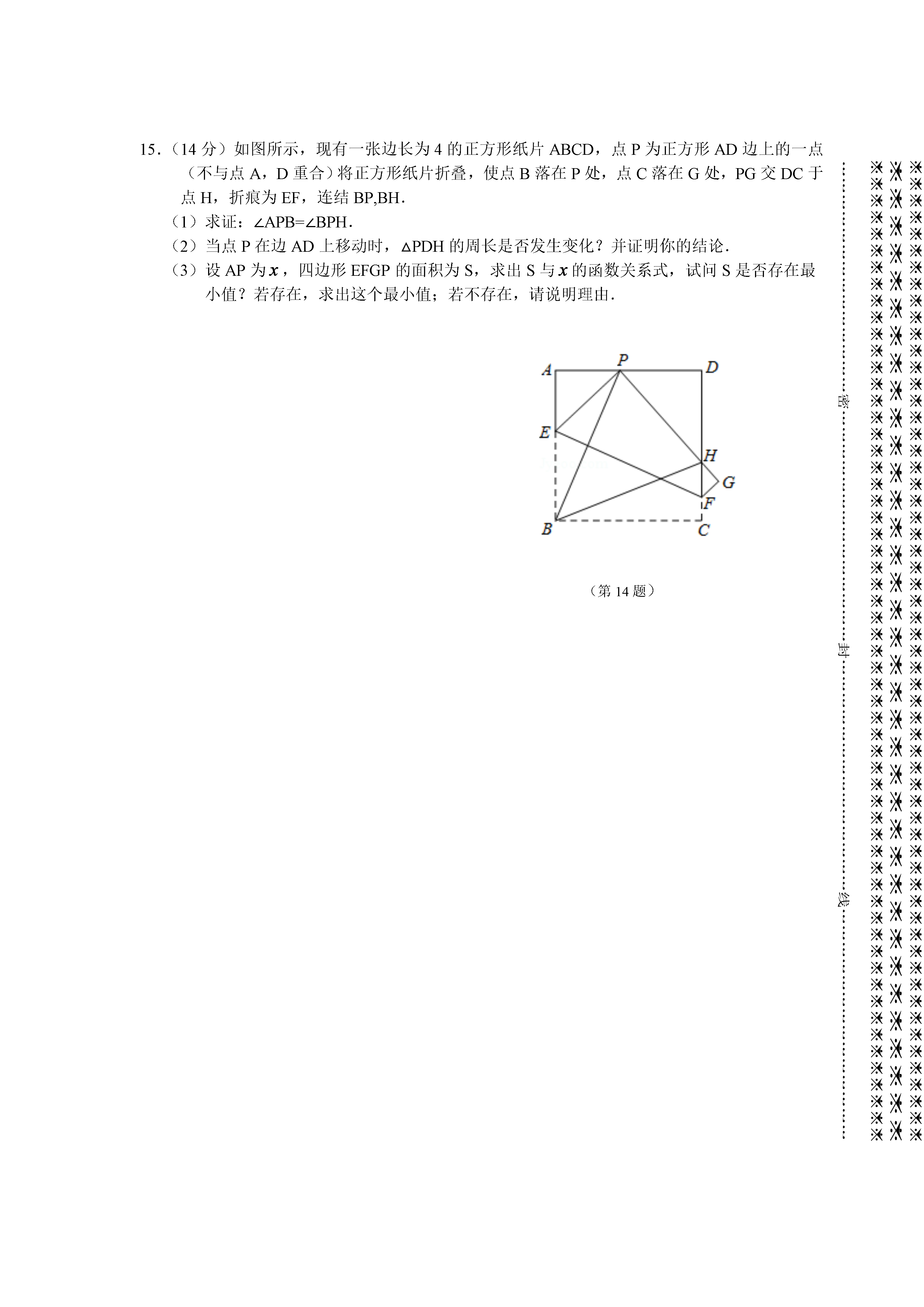
初中数学教师学科知识竞赛.doc
初中数学教师学科知识竞赛试卷一、选择题(共5小题,每小题5分,满分25分.每小题的四个选项中有且只有一个选项是正确的.请将正确选项的代号填入题后的括号里.不填、多填或错填均得零分)(第1题)1.如图,一个大长方形被两条线段AB,CD分成四个小长方形.如果其中图形Ⅰ、Ⅱ、Ⅲ的面积分别为8,6,5,那么图中阴影部分的面积为()A.B.C.D.如图,C在以AB为直径的半圆⊙上,是的内心,的延长线分别交半圆⊙于点D,E,AB=6,则DE的长为()(第2题)A.B.C.D.3.对于每个,函数是这三个函数中的最小值.
初中数学教师学科知识竞赛.pdf
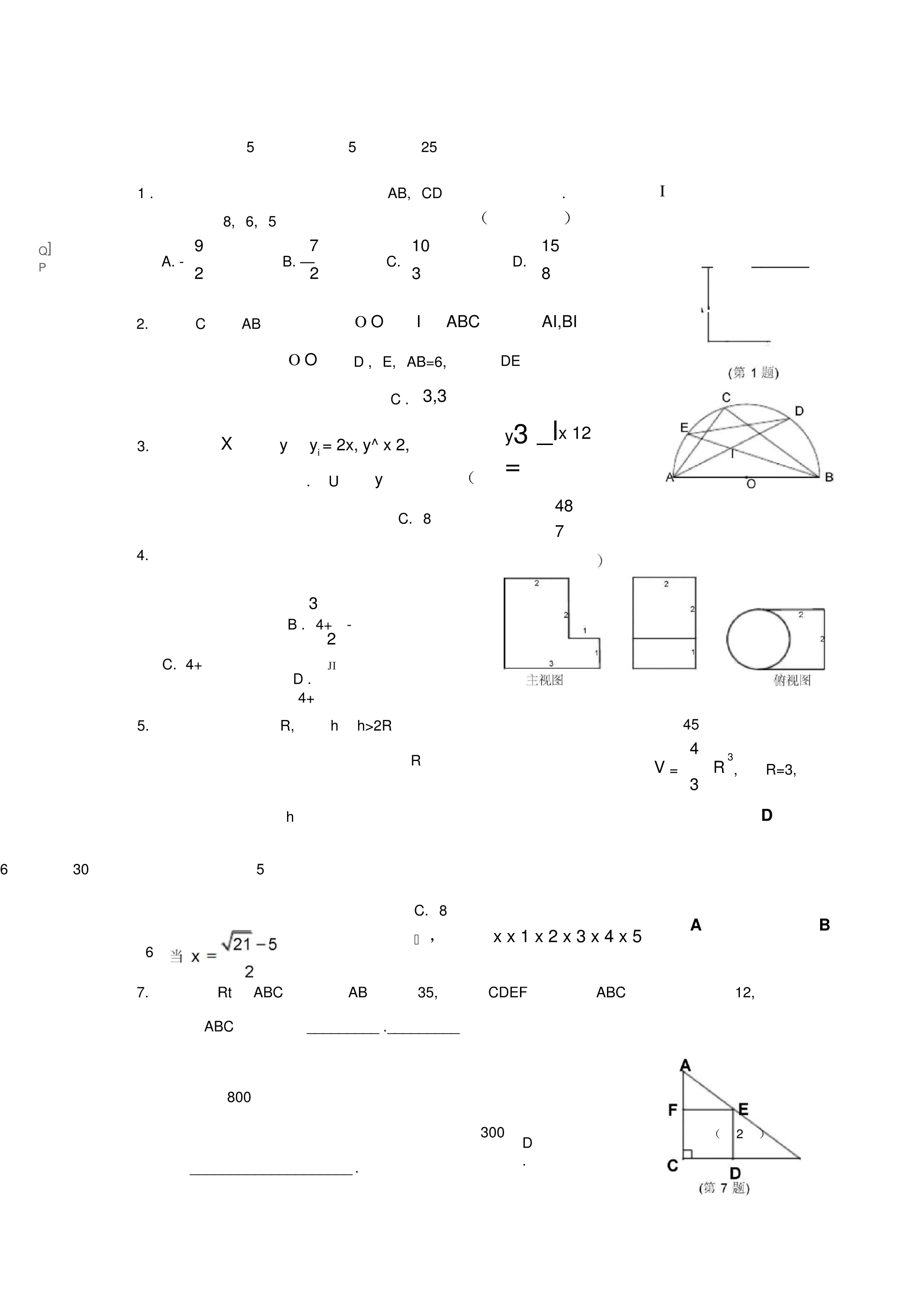
5小题,每小题5分,满分25分•每小题的四个选项中有且只有一个选项是正1.如图,一个大长方形被两条线段AB,CD分成四个小长方形.如果其中图形I、□、川积分别为8,6,5,那么图中阴影部分的面积为()的面Q]971015PA.-B.—C.D.2238■2.如图,C在以AB为直径的半圆OO上,I是ABC的内心,AI,BI—的延长线分别交半圆OO于点D,E,AB=6,则DE的长为(C.3,3y_lx123.对于每个X,函数y是y=2x,y^x2,3i=这三个函数中的最小值.贝U函数y的最大值是(48C.874

初中数学教师学科知识竞赛试题(含答案).pdf
初中数学教师学科知识竞赛试题◎◎◎◎◎◎一二三◎题号总分◎1-89-1415161718◎◎得分◎◎◎一、选择题(共8小题,每小题5分,满分40分.每小题有且只有一个选项是正确的)◎◎1.若关于x的方程(2ab)x10无解,则ab的值为()◎线◎A.负数B.正数C.非负数D.非正数◎号◎a22abb2b考◎2.抛物线yax2(ab)xb如图1所示,那么化简的结果是()◎a◎◎a2b2ba◎A.B.C.1D.-1◎aa◎.如图,在梯形中,,∠0°,M是AB的中点,若CM=6.5,BC

2010年永嘉县初中数学教师学科知识竞赛试卷.doc
学校姓名准考证号…………………………………装………………………………订………………………………………线………………………线…………………………………………2010年永嘉县初中数学教师学科知识竞赛试卷(时间:2010年10月23日上午9:00~11:00满分:120可带计算器)一、选择题(每小题5分,共30分)1.已知,,,则的值为()A.2B.3C.4D.52.如图,是双曲线上的三点,过这三点分别作y轴的垂线,得三个三角形,设它们的面积分别是S1,S2,S3,则()(第2题)A.B.C.D.3.关于的不等

2024年永嘉县初中数学教师学科知识竞赛试卷.pdf
