
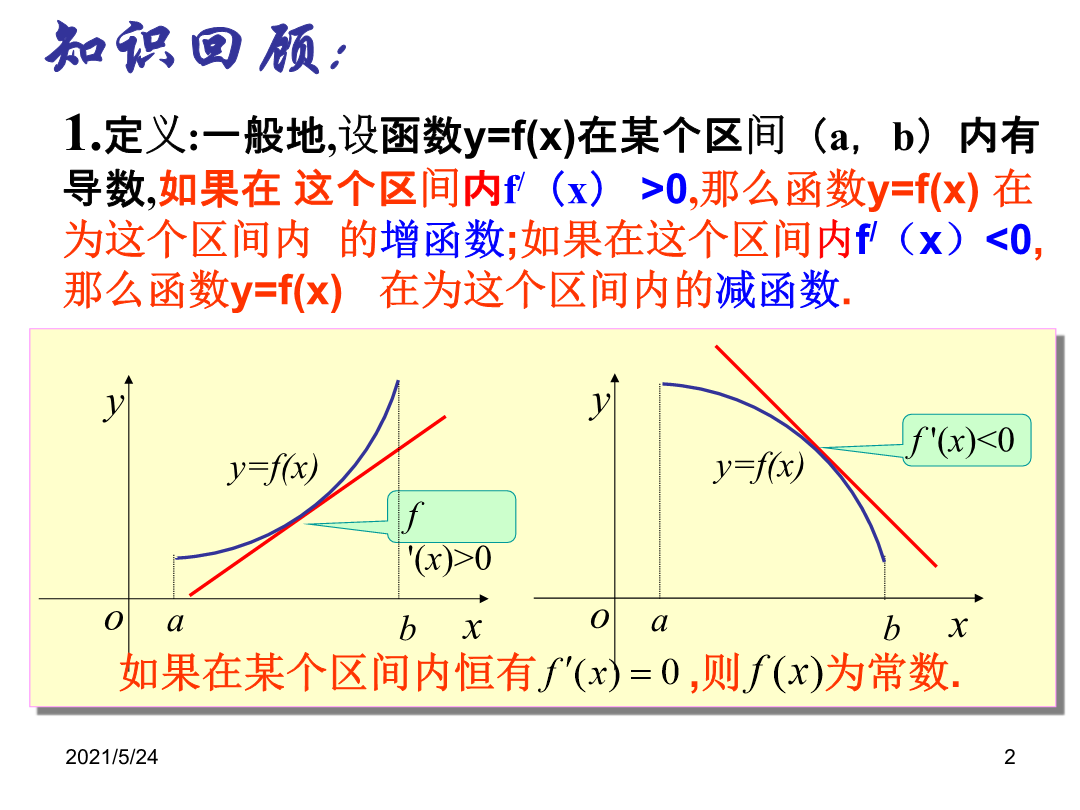
1.3.2函数的极值与导数(完美版).ppt

胜利****实阿





亲,该文档总共28页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

1.3.2函数的极值与导数(完美版).ppt
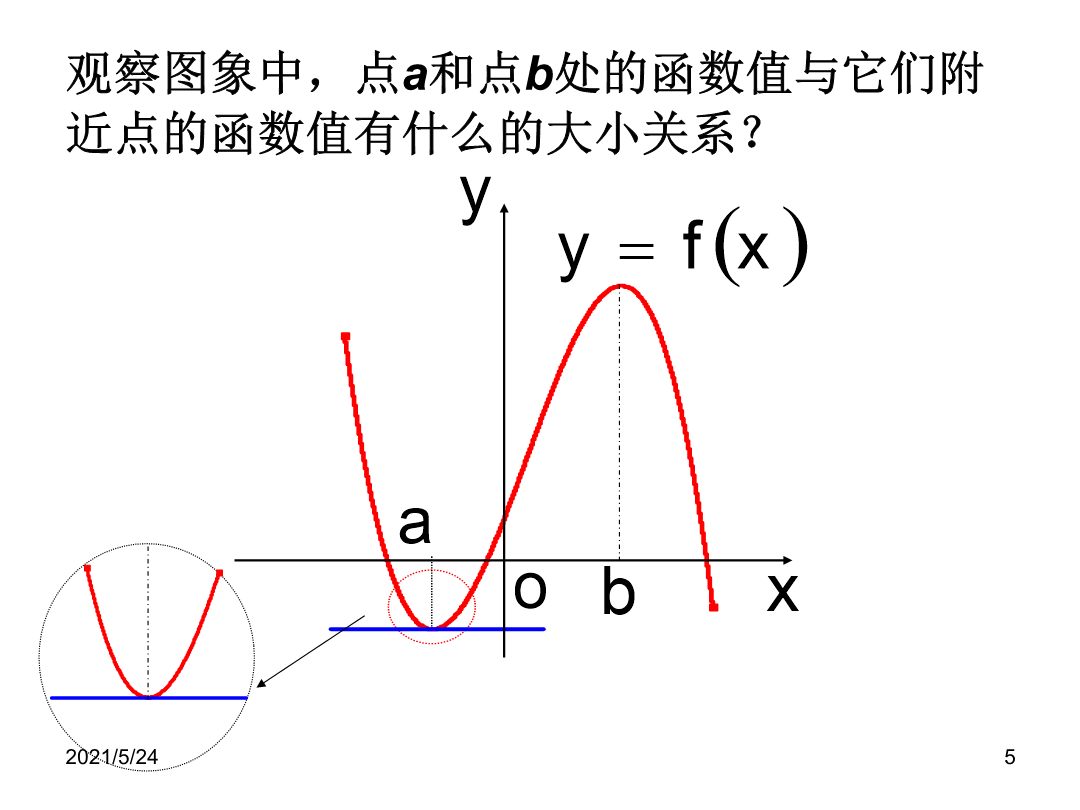
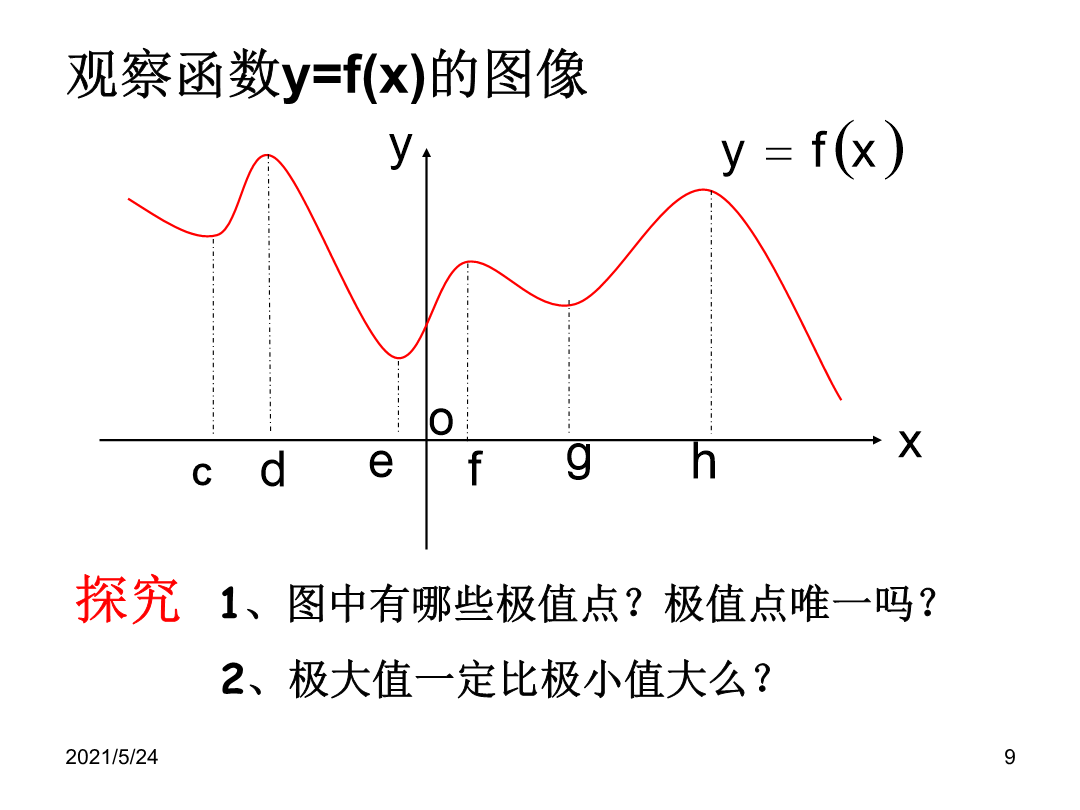
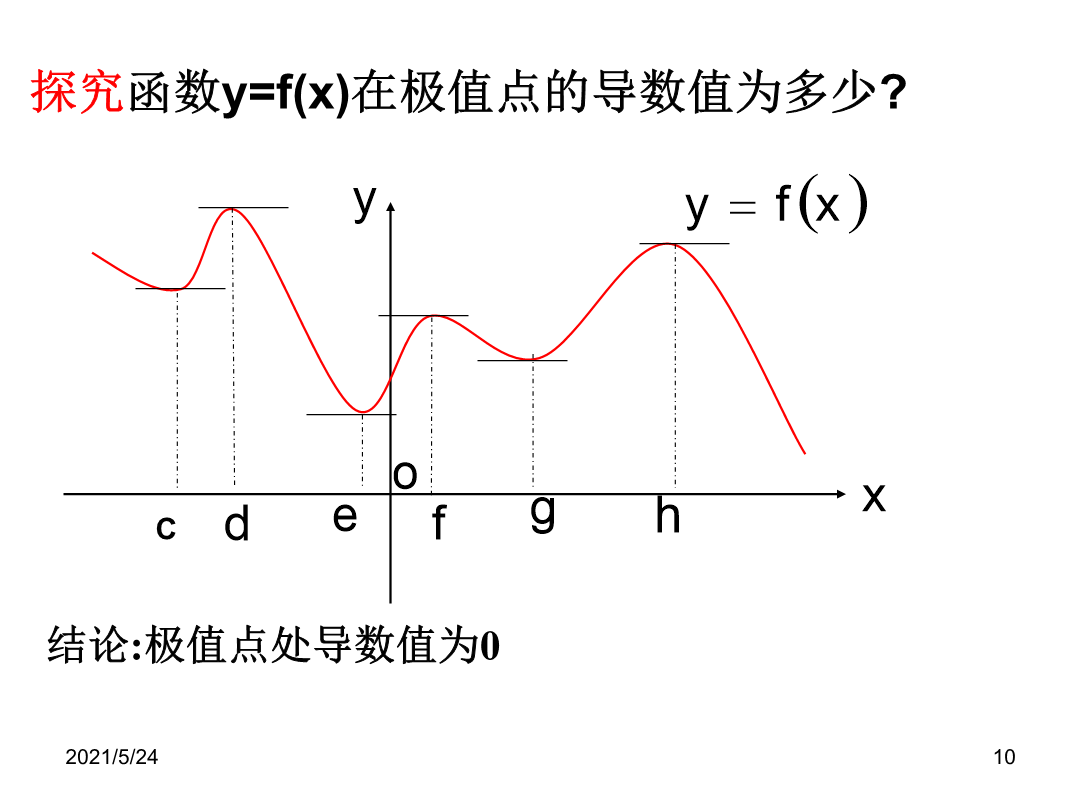
函数的极值与导数2.求函数单调性的一般步骤关注用导数本质及其几何意义解决问题观察图象中,点a和点b处的函数值与它们附近点的函数值有什么的大小关系?新课讲解——函数的极值:极值的定义函数极值是在某一点附近的小区间内定义的,是局部性质。因此一个函数在其整个定义区间上可能有多个极大值或极小值,并对同一个函数来说,在某一点的极大值也可能小于另一点的极小值。观察函数y=f(x)的图像结论:极值点处导数值为0探究极值点两侧导数符号有何规律?结论若x0满足f/(x)=0,且在x0的两侧的导数异号,则x0是f(x)的极值

1.3.2函数的极值与导数(上课).ppt

《1.3.2函数的极值与导数》同步练习2.doc
《1.3.2函数的极值与导数》同步练习一、选择题1.函数f(x)的定义域为开区间(a,b),导数f′(x)在(a,b)内的图象如下图所示,则函数f(x)在开区间(a,b)内极小值有()A.1个B.2个C.3个D.4个答案:A2.下列关于函数的极值的说法正确的是()A.导数值为0的点一定是函数的极值点B.函数的极小值一定小于它的极大值C.函数在定义域内有一个极大值和一个极小值D.若f(x)在(a,b)内有极值,那么f(x)在(a,b)内不是单调函数解析:导数值为0的点不一定是极值点,如y=x3,y′=3x2

《1.3.2 利用导数研究函数的极值》同步练习2.doc
《1.3.2利用导数研究函数的极值》同步练习21.函数y=2x3-3x2()A.在x=0处取得极大值0,但无极小值B.在x=1处取得极小值-1,但无极大值C.在x=0处取得极大值0,在x=1处取得极小值-1D.以上都不对解析:y'=6x(x-1),令y'=0,得x=0,或x=1.当x变化时,f'(x),f(x)的变化情况如下表:x(-∞,0)0(0,1)1(1,+∞)f'(x)+0-0+f(x)单调递增↗0单调递减↘-1单调递增↗所以当x=0时有极大值f(0)=0,当x=1时有极小值f(1)=-1.答案:

《1.3.2 利用导数研究函数的极值》导学案3.doc
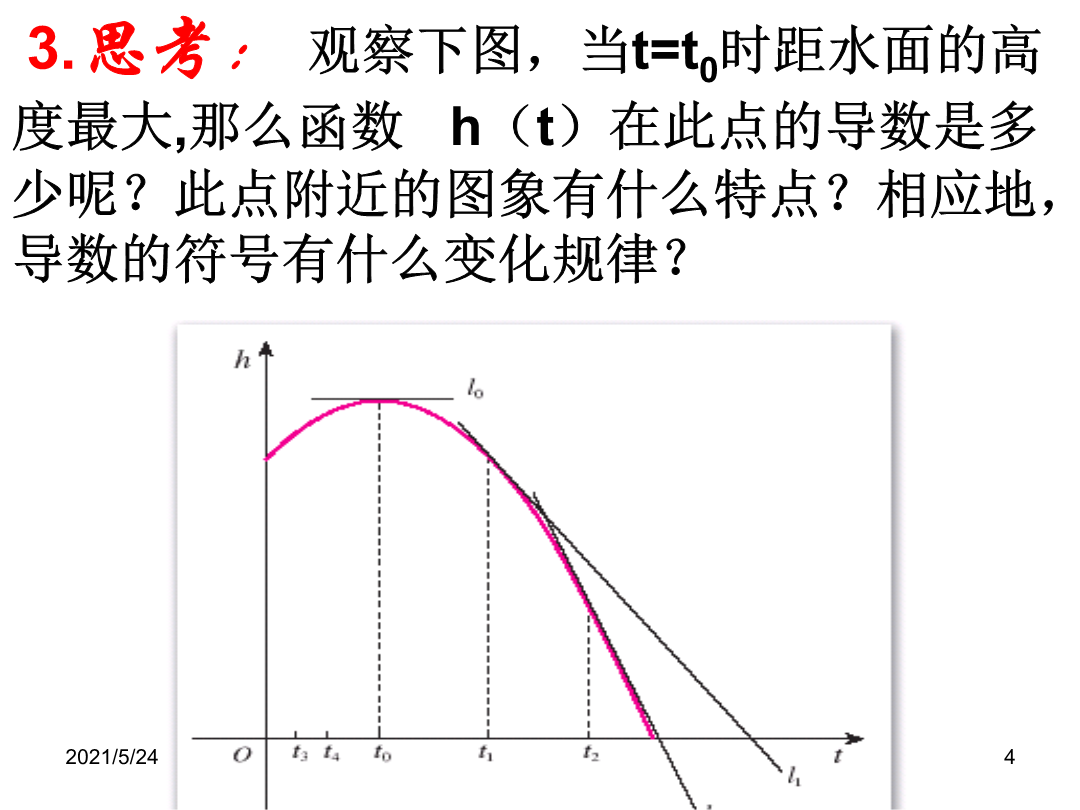
《1.3.2利用导数研究函数的极值》导学案3【学习目标】1.会从几何直观了解函数极值和导数的关系;2.能利用导数研究函数的极值;【学习重点】函数极值和导数的关系;【学习难点】函数在某点取得极值的必要条件和充分条件;【问题导学】1.群山之中,各个山峰的顶端虽然不一定是群山的最高处,但它却是其附近的最高点。同样,各个山谷底虽然不一定是群山之中的最低处,但它却是附近的最低点。数学中也有这种现象,例如3.3.1函数的单调性与导数“观察”栏目中的跳水问题。观察3.3-1(1),我们发现,当t=a时,高台跳水运动员距
