1.3.2函数的极值与导数(上课).ppt

2024-05-12

15

1.3MB

1.3.2函数的极值与导数教学反思.doc

1.3.2函数的极值与导数教学反思1.3.2函数的极值与导数教学反思1.3.2函数的极值与导数教学反思《1.3。2函数的极值与导数》的教学反思应用函数极值与导数的关系求函数极值，用导数求闭区间上函数的最大值和最小值的方法让学生经过实例分析,熟练灵活掌握，使学生经历知识产生与形成的过程.以自主探究为主，及时归纳方法，熟练灵活应用知识解决问题，注意题型归类．规范解题步骤，严格化训练学生运算能力。加强自信心的培养，积累高考题、创新题的解法，鼓励学生从多个角度分析解决问题，形成良好的知识结构与网络。通过自主探究、

2024-11-07

10

11KB

函数的极值与导数(上课).ppt

编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件编辑课件

2024-08-12

20

1.2MB

1.3.2函数的极值与导数(完美版).ppt

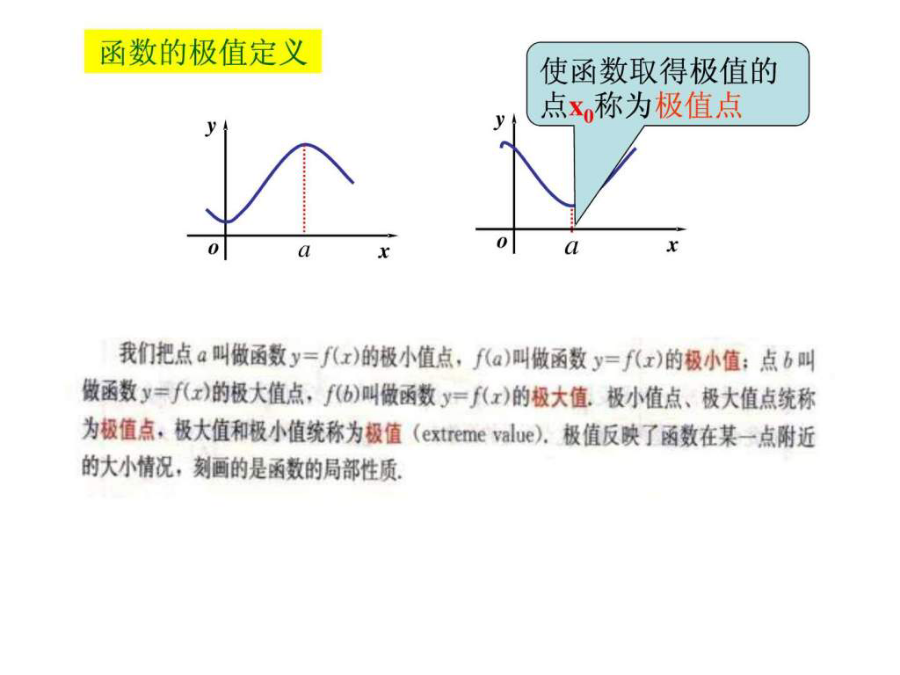
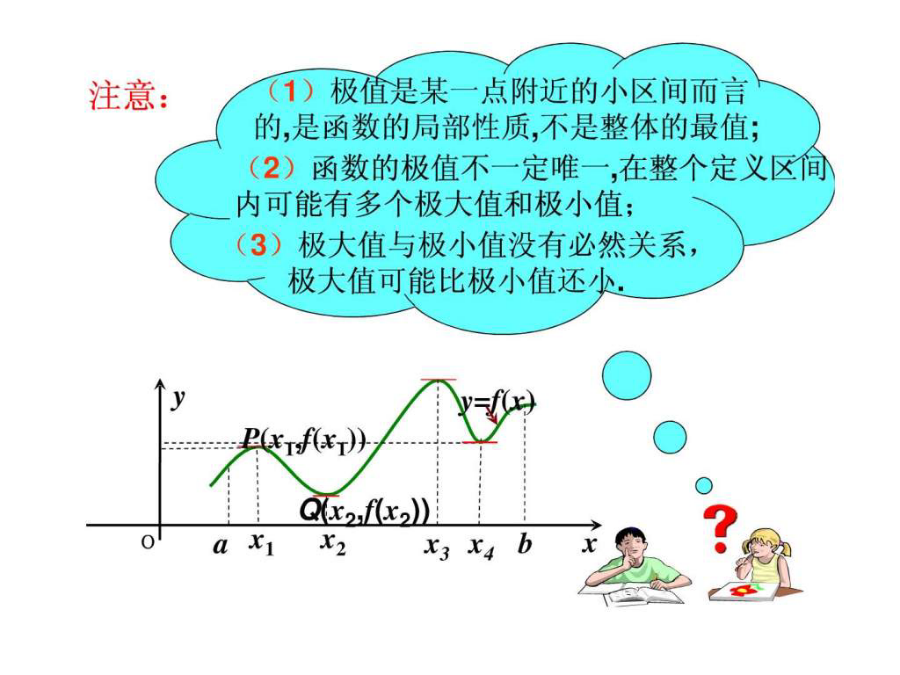
函数的极值与导数2.求函数单调性的一般步骤关注用导数本质及其几何意义解决问题观察图象中，点a和点b处的函数值与它们附近点的函数值有什么的大小关系？新课讲解——函数的极值:极值的定义函数极值是在某一点附近的小区间内定义的，是局部性质。因此一个函数在其整个定义区间上可能有多个极大值或极小值，并对同一个函数来说，在某一点的极大值也可能小于另一点的极小值。观察函数y=f(x)的图像结论:极值点处导数值为0探究极值点两侧导数符号有何规律?结论若x0满足f/(x)=0,且在x0的两侧的导数异号,则x0是f(x)的极值

2024-01-17

11

343KB

《1.3.2函数的极值与导数》同步练习2.doc

《1.3.2函数的极值与导数》同步练习一､选择题1.函数f(x)的定义域为开区间(a，b)，导数f′(x)在(a，b)内的图象如下图所示，则函数f(x)在开区间(a，b)内极小值有()A.1个B.2个C.3个D.4个答案:A2.下列关于函数的极值的说法正确的是()A.导数值为0的点一定是函数的极值点B.函数的极小值一定小于它的极大值C.函数在定义域内有一个极大值和一个极小值D.若f(x)在(a，b)内有极值，那么f(x)在(a，b)内不是单调函数解析:导数值为0的点不一定是极值点，如y=x3，y′=3x2

2024-09-28

16

82KB