三次样条插值.ppt

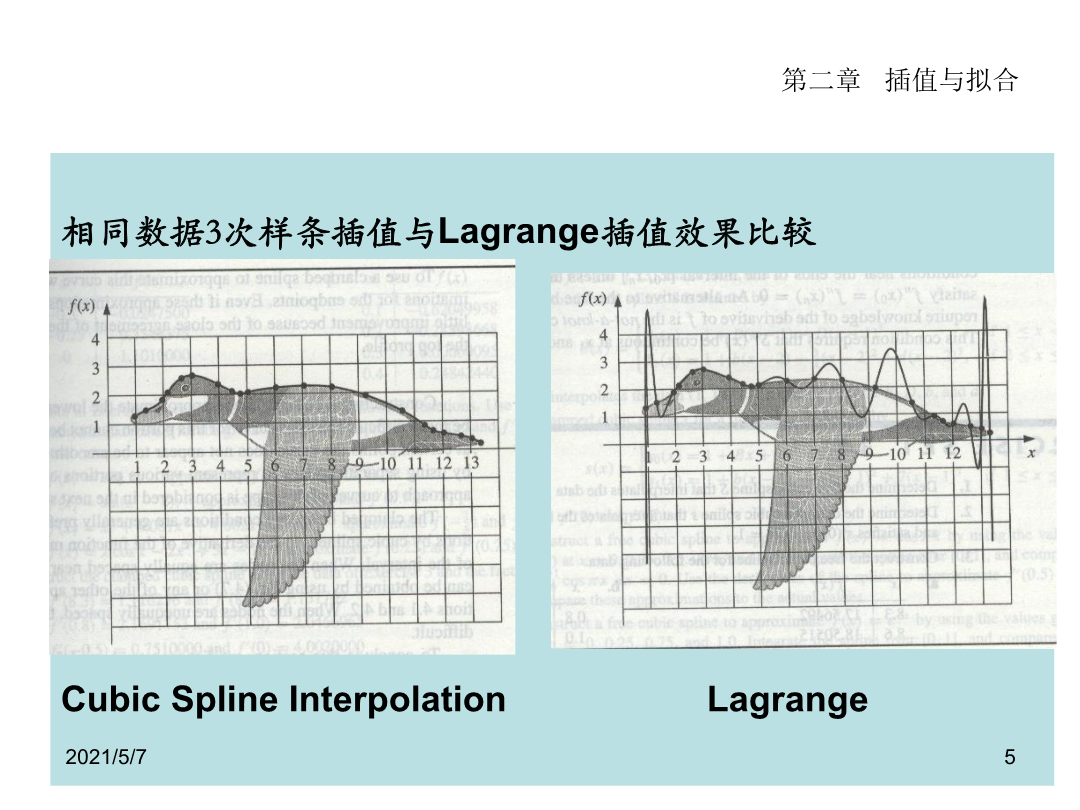
三次样条插值高次插值出现龙格现象数学里的样条(Spline)一词来源于它的直观几何背景：绘图员或板金工人常用弹性木条或金属条加压铁(构成样条!)固定在样点上，在其它地方让它自由弯曲，然后画下长条的曲线，称为样条曲线.样条曲线实际上是由分段三次曲线并接而成，在连接点击样点上要求二阶导数连续，从数学上加以概括就得到数学样条这一概念。相同数据3次样条插值与Lagrange插值效果比较CubicSplineInterpolationLagrange定义2.8（三次样条函数）提出问题：构造方法：S(x)应具有如下形式并且满足条件(2.42)和分析：第3种边界条件（周期边界条件）：这样，由以上给定的任一种边界条件加上插值条件和连接条件，就能得出4n个方程，可以惟一确定4n个系数。从而得到三次样条插值函数S(x)在各个子区间xi,xi+1上的表达式S(xi）(i=1,2,…,)。但是，这种做法当n较大时，计算工作很大，不便于实际应用。因此我们希望找到一种简单的构造方法。推导方法：------三次样条插值函数的二阶导数表示由两点拉格朗日插值可表示为将上式代入(2.48)得到三次样条插值函数的表达式2021/5/72021/5/7（2.55）所得方程可简写成这是一个含有n+1个未知数、n-1个方程的线性方程组.要完全确定Mi(i=0,1,…,n)的值还需要补充两个条件,这两个条件通常根据实际问题的需要，根据插值区间a,b的两个端点处的边界条件来补充。由(2.53),得2021/5/7(2)若(3)对第三类边界条件：令2021/5/7说明：例2.14设在节点上，函数的值为，。试求三次样条插值函数，满足条件对第一类边界条件（２）仍用方程组进行求解，不过要注意的不同。由于和已知，故可以化简得由此解得。例2.15已知的函数值如下：x1245f(x)1342根据给定数据和边界条件算出与则得方程组同理S(x)在上的表达式为故所求的三次样条插值函数S(x)在区间上的表达式为下面构造一阶导数值表示的三次样条插值函数。在力学上解释为细梁在截面处的转角，并且得到的转角与相邻两个转角有关，故称用表示的算法为三转角算法。根据Hermite插值函数的唯一性和表达式可设S(x)在区间[xi,xi+1](i=0,1,…n-1)的表达式为对S(x)求二次导数得利用条件，得由此可解得m1,m2,…,mn-1，从而得S(x)的表达式.①对于边界条件(2.44),可导出两个方程:若令由(2.62)和(2.67)可解出，方程组的矩阵形式为在实际应用中，如果不需要规定内节点处的一阶导数值，那么使用三次样条插值函数会得到很好的效果。三次样条插值函数不仅在内节点处的二阶导数是连续的，而且逼近具有很好的收敛性，也是数值稳定的。由于误差估计与收敛性定理的证明比较复杂，下面只给出误差估计的结论。