
基于matlab的Lorenz系统仿真研究.doc

胜利****实阿




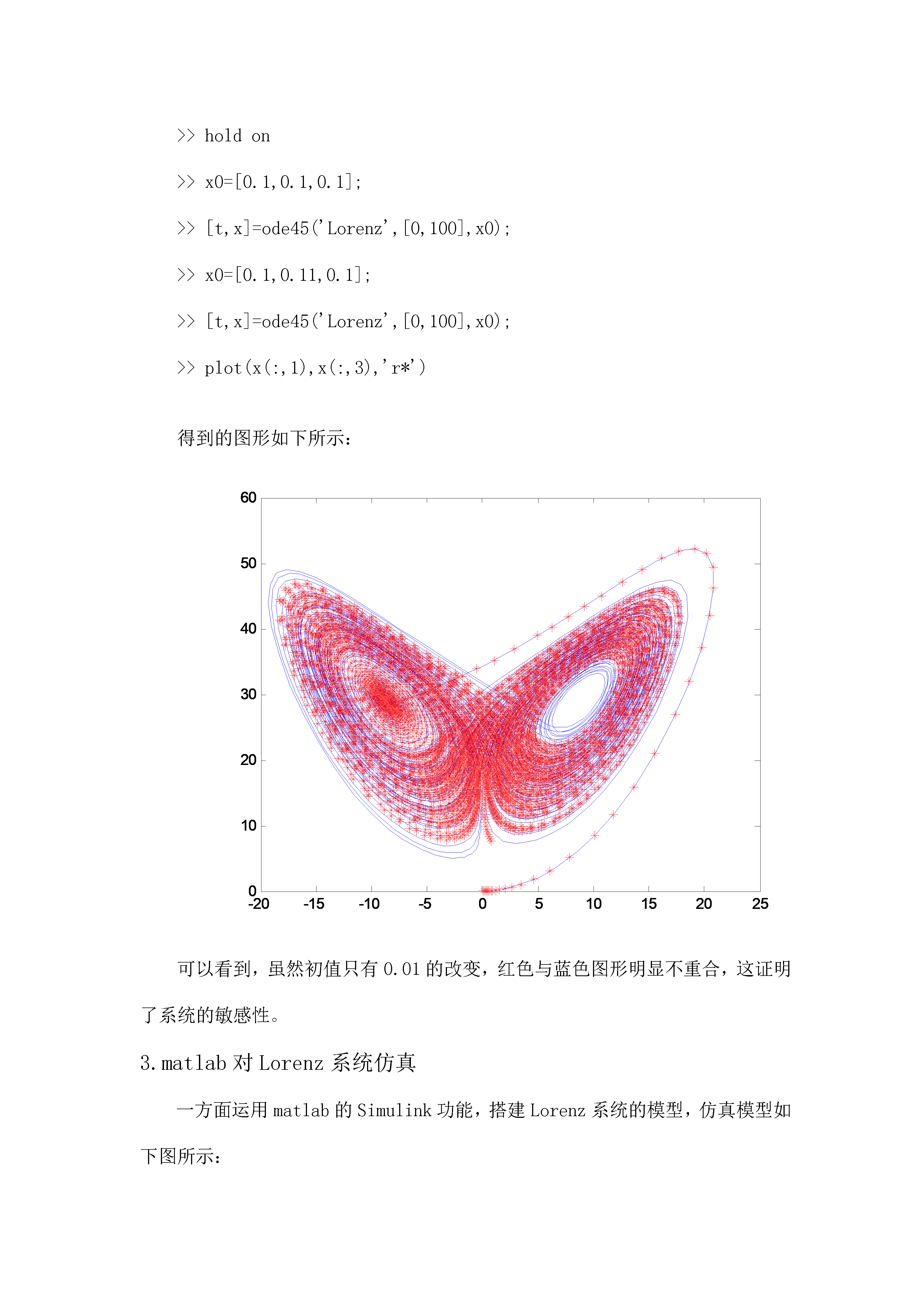
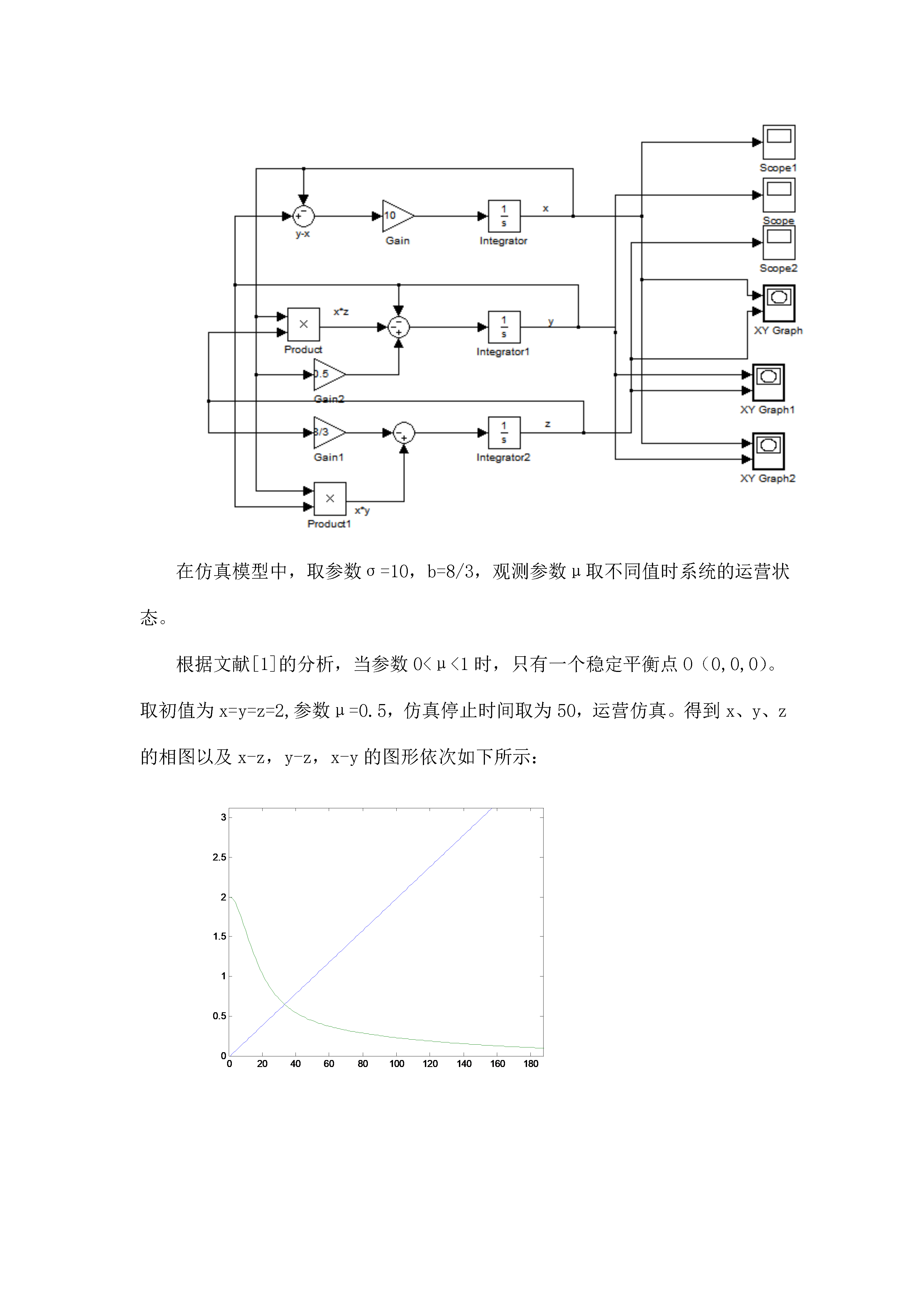


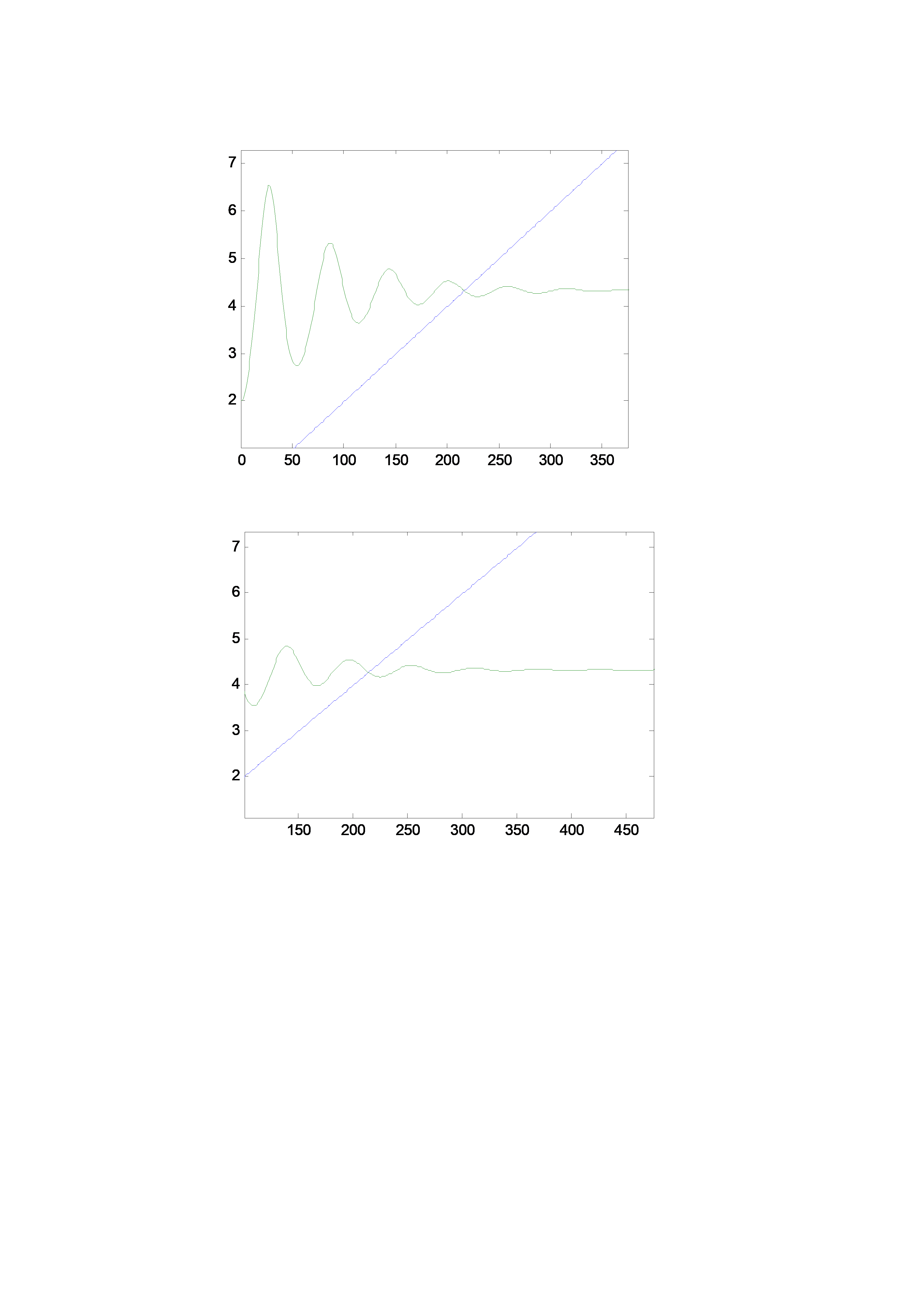

亲,该文档总共27页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

基于matlab的Lorenz系统仿真研究.doc
基于Matlab的Lorenz系统仿真研究摘要:本文运用matlab这一数学工具对Lorenz系统进行了研究。一方面使用matlab分析求解Lorenz方程,运用matlab的绘图功能,直观地观测了Lorenz混沌吸引子的三维图形,并简朴观测了Lorenz混沌系统对初值的敏感性;然后对Lorenz系统进行仿真,比较分析在不同参数下的Lorenz系统仿真结果;最后验证了通过添加反馈控制的方式,可以使Lorenz方程不稳定的平衡点成为稳定的平衡点。关键词:Lorenz系统;matlab;混沌系统1.引言Lor

基于matlab的Lorenz系统的仿真研究.docx
MATLAB课程期末作业以下报告完成的是大作业第七题:7.Simulink仿真在高等数学课程中的应用21130223宋沛儒基于MATLAB/Simulink对Lorenz系统仿真研究21130223宋沛儒1.引言1963年Lorenz通过观察大量大气现象并进行数值实验和理论思考,得到了一系列混沌运动的基本特征,提出了第一个奇异吸引子—Lorenz吸引子[1],Lorenz通过计算机模拟一个由三阶微分方程描述的天气模型时发现,在某些条件下同一个系统可以表现出非周期的无规则行为。Lorenz揭示了一系列混沌运

基于matlab的Lorenz系统仿真研究.docx
基于Matlab的Lorenz系统仿真研究摘要:本文利用matlab这一数学工具对Lorenz系统进行了研究。首先使用matlab分析求解Lorenz方程,利用matlab的绘图功能,直观地观察了Lorenz混沌吸引子的三维图形,并简单观察了Lorenz混沌系统对初值的敏感性;然后对Lorenz系统进行仿真,比较分析在不同参数下的Lorenz系统仿真结果;最后验证了通过添加反馈控制的方式,可以使Lorenz方程不稳定的平衡点成为稳定的平衡点。关键词:Lorenz系统;matlab;混沌系统1.引言Lore

基于matlab的Lorenz系统仿真研究样本.doc
基于MatlabLorenz系统仿真研究摘要:本文运用matlab这一数学工具对Lorenz系统进行了研究。一方面使用matlab分析求解Lorenz方程,运用matlab绘图功能,直观地观测了Lorenz混沌吸引子三维图形,并简朴观测了Lorenz混沌系统对初值敏感性;然后对Lorenz系统进行仿真,比较分析在不同参数下Lorenz系统仿真成果;最后验证了通过添加反馈控制方式,可以使Lorenz方程不稳定平衡点成为稳定平衡点。核心词:Lorenz系统;matlab;混沌系统1.引言Lorenz方程是由美

基于matlab的Lorenz系统仿真研究样本.doc
基于MatlabLorenz系统仿真研究摘要:本文运用matlab这一数学工具对Lorenz系统进行了研究。一方面使用matlab分析求解Lorenz方程,运用matlab绘图功能,直观地观测了Lorenz混沌吸引子三维图形,并简朴观测了Lorenz混沌系统对初值敏感性;然后对Lorenz系统进行仿真,比较分析在不同参数下Lorenz系统仿真成果;最后验证了通过添加反馈控制方式,可以使Lorenz方程不稳定平衡点成为稳定平衡点。核心词:Lorenz系统;matlab;混沌系统1.引言Lorenz方程是由美
