第6章 抽样推断.ppt

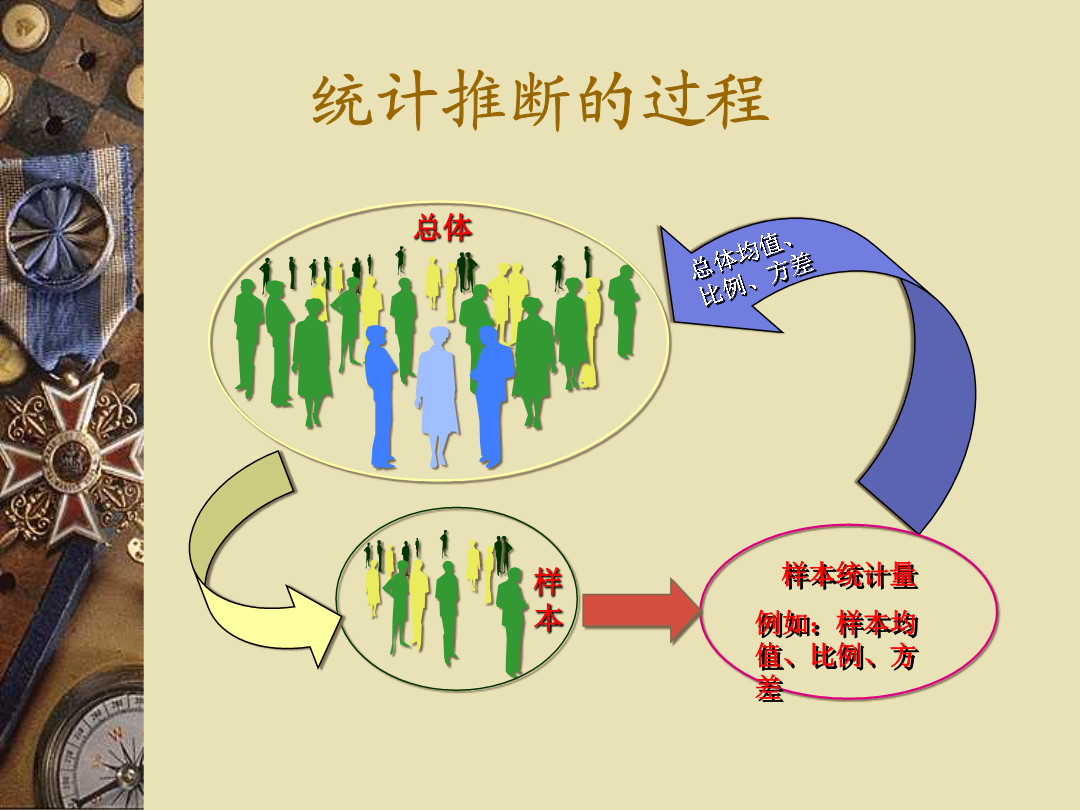
第六章抽样推断第六章抽样推断第一节抽样推断有关概念与理论依据统计推断的过程（二）特点(三)抽样推断的内容二、抽样推断的作用1.实际工作不可能进行全面调查观察而又需要了解其全面资料的事物；三、抽样推断的基本概念(二)抽样方法(三)参数和统计量（全及指标和抽样指标、总体指标和样本指标)研究数量标志(四)样本容量——指一个样本所包括的单位数。(六)样本个数——指从总体中可能抽取的最多的样本数量。考虑顺序置信度也称为可靠度或置信水平、置信系数。即在抽样对总体参数作出估计时由于样本的随机性其结论总是不确定的。因此采用一种概率的陈述方法也就是数理统计中的区间估计法即估计值与总体参数在一定允许的误差范围以内其相应的概率有多大这个相应的概率称作置信度。(一)大样本统计量分布的依据-中心极限定理（2）正态分布的分布函数若对其进行“标准化”变换即令则2、中心极限定理(1)独立同分布的中心极限定理定理的应用：对于独立的随机变量序列不管服从什么分布只要它们是同分布且有有限的数学期望和方差那么当n充分大时这些随机变量之和近似地服从正态分布(2)棣莫弗—拉普拉斯中心极限定理一般地1、t分布及小样本均值的分布律设随机变量X～N(01)Y～2(n)且X与Y相互独立则称统计量当n较大时t分布近似于标准正态分布.设(X1X2…Xn)为来自正态总体X～N(2)的样本则统计量设(X1X2…Xn1)和(Y1Y2…Yn2)分别是来自正态总体N(12)和N(22)的样本且它们相互独立则统计量——分布五、抽样推断的基本原理总体方差已知时总体均值μ的区间估计对于给定的置信概率即在给定的显著性水平下总体均值在的置信概率下的置信区间为第二节抽样误差抽样误差即指随机误差这是抽样调查固有的误差是无法避免的。抽样误差的作用：二、抽样平均误差（二）理论公式例（三）实际计算公式（以纯随机抽样为例）总体方差未知时解决方法：某灯泡厂从一天所生产的产品10000个中抽取100个检查其寿命得平均寿命为2000小时根据以往资料σ=20小时试求抽样平均误差。某玻璃器皿厂某日生产15000只印花玻璃杯现按重复抽样方法从中抽取150只进行质量检验有147只合格试求这批印花玻璃杯合格率的抽样平均误差。（四）影响抽样误差的因素：例：假定抽样单位数增加2倍、0.5倍时其他条件不变抽样平均误差怎样变化？例：假定抽样平均误差缩小40%时其他条件不变抽样单位数怎样变化？一、抽样极限误差根据中心极限定理得知当n足够大时抽样总体为正态分布根据正态分布规律可知样本指标是以一定的概率落在某一特定的区间内统计上把这个给定的区间叫抽样极限误差也称置信区间即在概率F(t)的保证下：当F(t)=68.27%时抽样极限误差等于抽样平均误差的1倍(t=1);当F(t)=95.45%时抽样极限误差等于抽样平均误差的2倍(t=2);当F(t)=99.73%时抽样极限误差等于抽样平均误差的3倍(t=3);上例资料编成次数分配表如下：-30样本个数样本频率样本累计频率05101520合计-30样本个数样本频率样本累计频率050.200.20580.320.521060.240.761540.160.922020.081.00合计251.00--（一）点估计