
空间力系分解.ppt

YY****。。



亲,该文档总共30页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

空间力系分解.pptx

空间力系分解.ppt
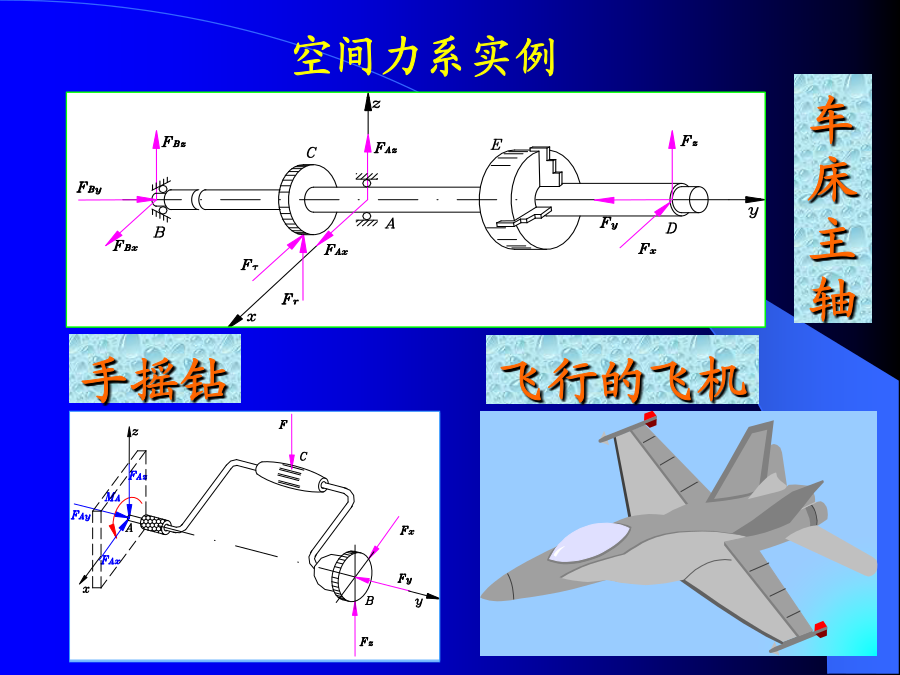
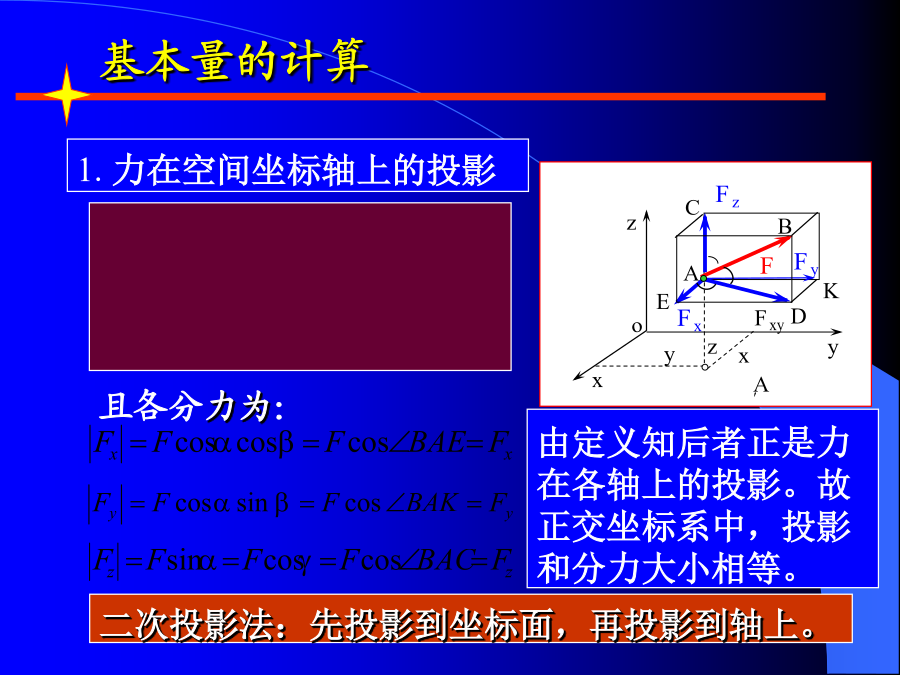
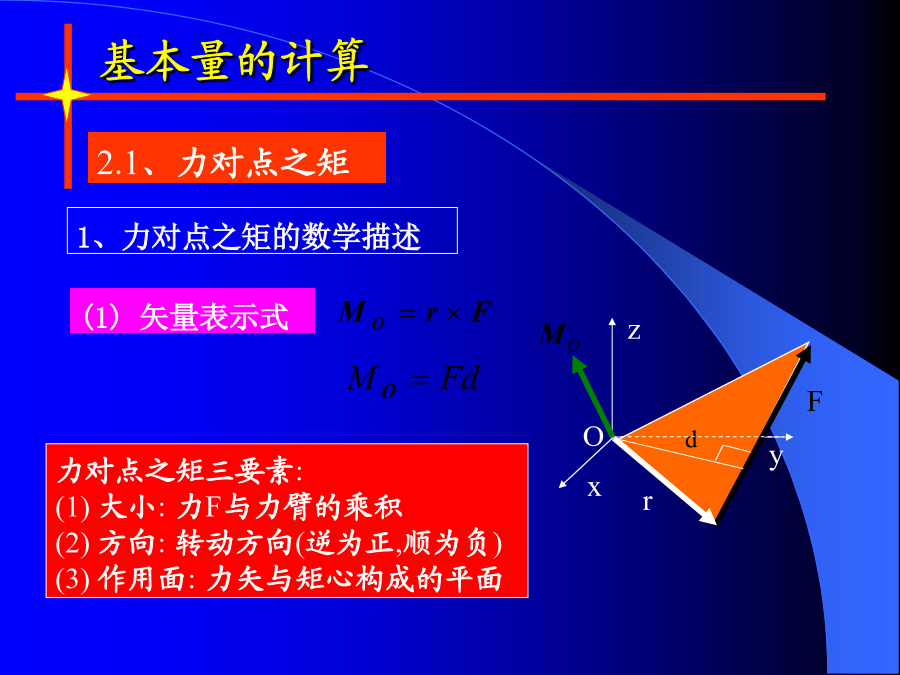
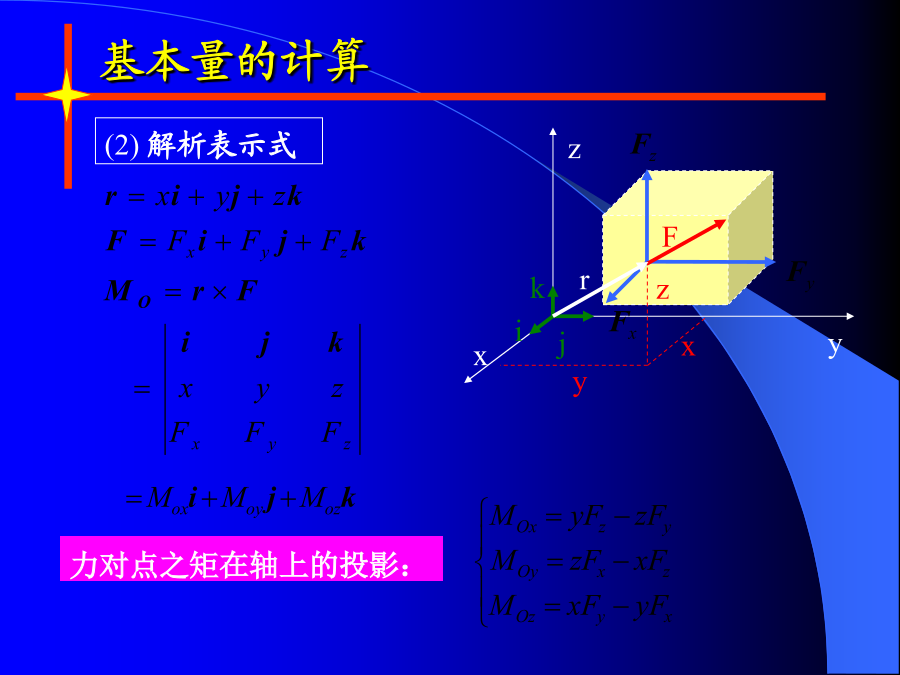
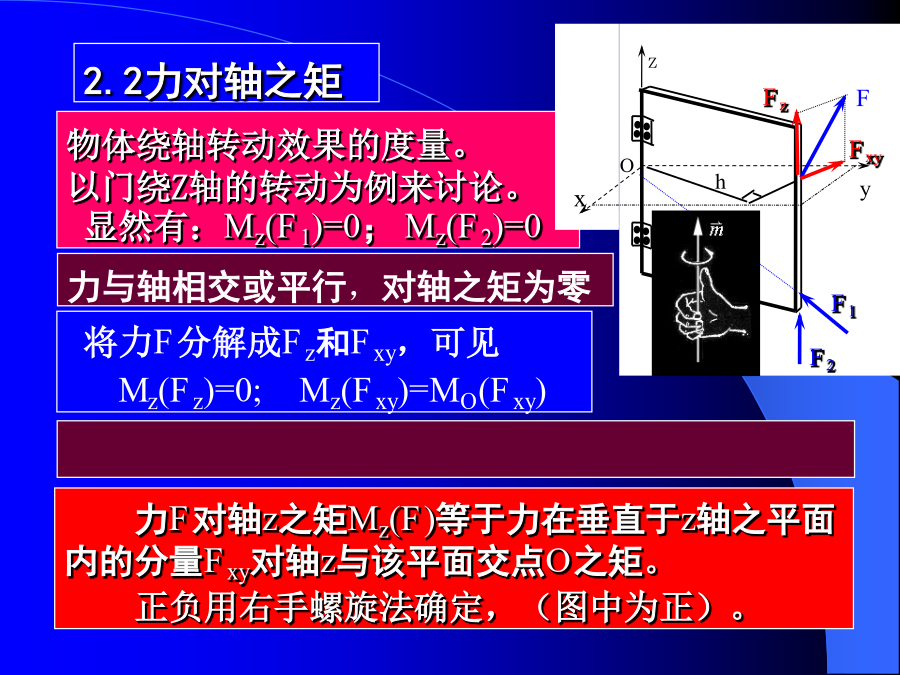
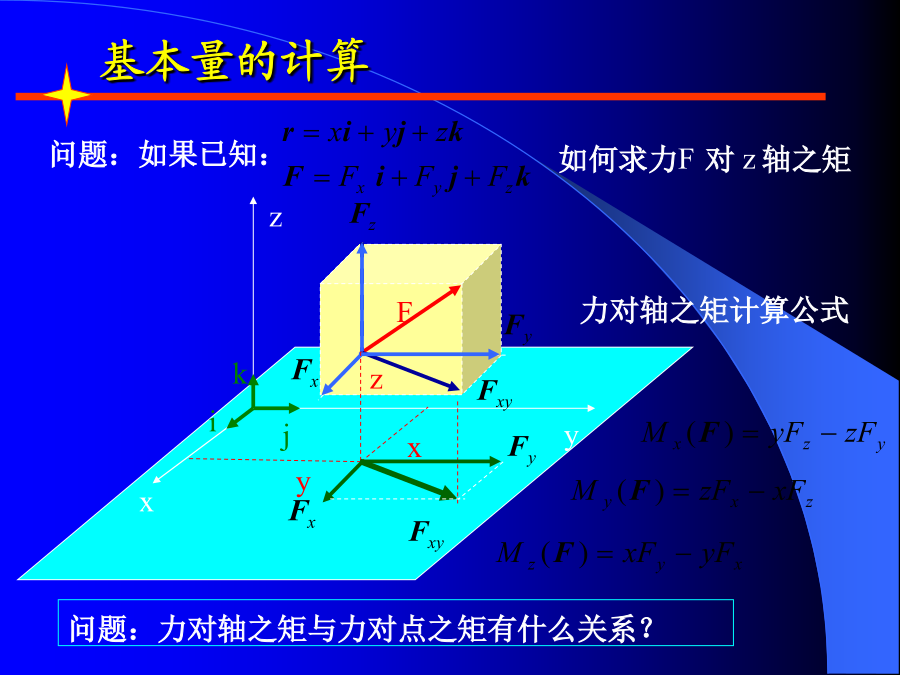
第三章空间力系空间力系实例1、空间汇交力系:各力作用线汇交于同一点(不含力偶)。(2)力对点之矩与力对轴之矩;力F为Fz、Fxy;FxyFx、Fy;显然有:F=Fx+Fy+Fz;x(2)解析表示式物体绕轴转动效果的度量。以门绕Z轴的转动为例来讨论。显然有:Mz(F1)=0;Mz(F2)=0问题:如果已知:力对轴之矩例:试写出图中力F在轴上的投影及对力轴之矩。3、力偶的矢量表示3.2、力偶的等效条件和性质二、力偶的性质性质三只要力偶矩矢量的方向和大小不变(F,d可变),则力偶对刚体的作用效应就不变。三、

空间力系及重心.doc
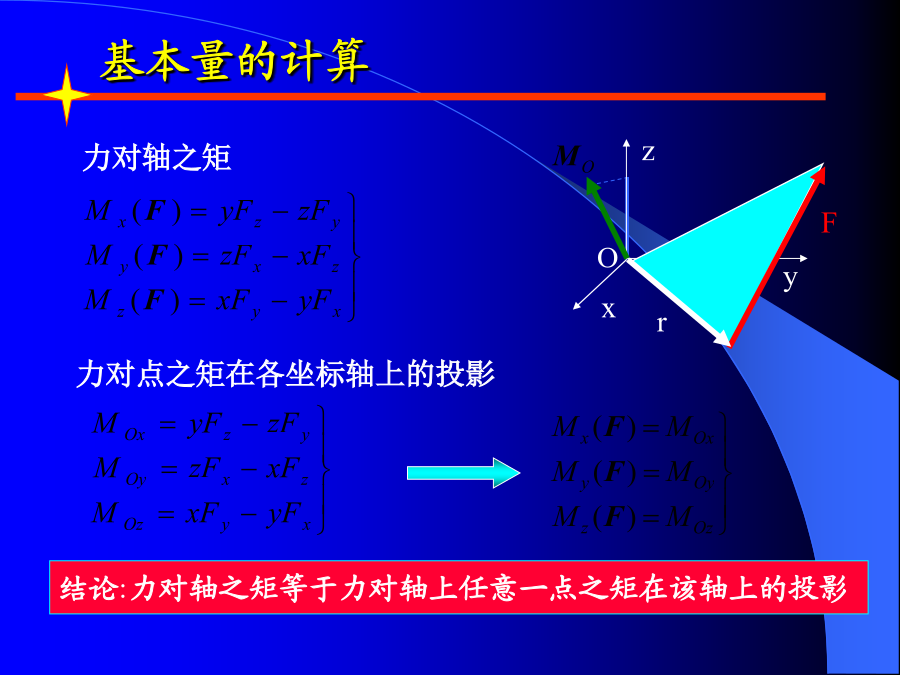
第六章空间力系及重心一、内容提要1、空间力对点之矩和对轴之矩1)空间力对点之矩是矢量,且2)空间力对轴之矩是一代数量,其正负号按右手螺旋规则确定,大小有两种计算方法:(a)先将力投影到垂直于轴的平面上,然后按平面上力对点之矩计算,即(b)若已知力在坐标轴上的投影Fx、Fy和FZ及该力的作用点的坐标x、y、z,则力对各坐标轴的矩可表示为yFz-zFyzFx-xFzxFy-yFx力对点之矩和力对轴之矩的关系(力矩关系定理):4)特殊情况当力与轴平行或相交(即力与轴共面)时,力对

空间力系分析.pptx

空间力系及重心.docx
第六章空间力系及重心一、内容提要1、空间力对点之矩和对轴之矩1)空间力对点之矩是矢量,且2)空间力对轴之矩是一代数量,其正负号按右手螺旋规则确定,大小有两种计算方法:(a)先将力投影到垂直于轴的平面上,然后按平面上力对点之矩计算,即(b)若已知力在坐标轴上的投影Fx、Fy和FZ及该力的作用点的坐标x、y、z,则力对各坐标轴的矩可表示为yFz-zFyzFx-xFzxFy-yFx力对点之矩和力对轴之矩的关系(力矩关系定理):4)特殊情况当力与轴平行或相交(即力与轴共面)时,力对轴之矩等于零。2、空间任意力系的
