内容提供者
八下171勾股定理(第1课时).ppt
2024-11-07
10金币
383KB
18页
lj****88
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
亲，该文档总共18页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
八下171勾股定理(第1课时).ppt
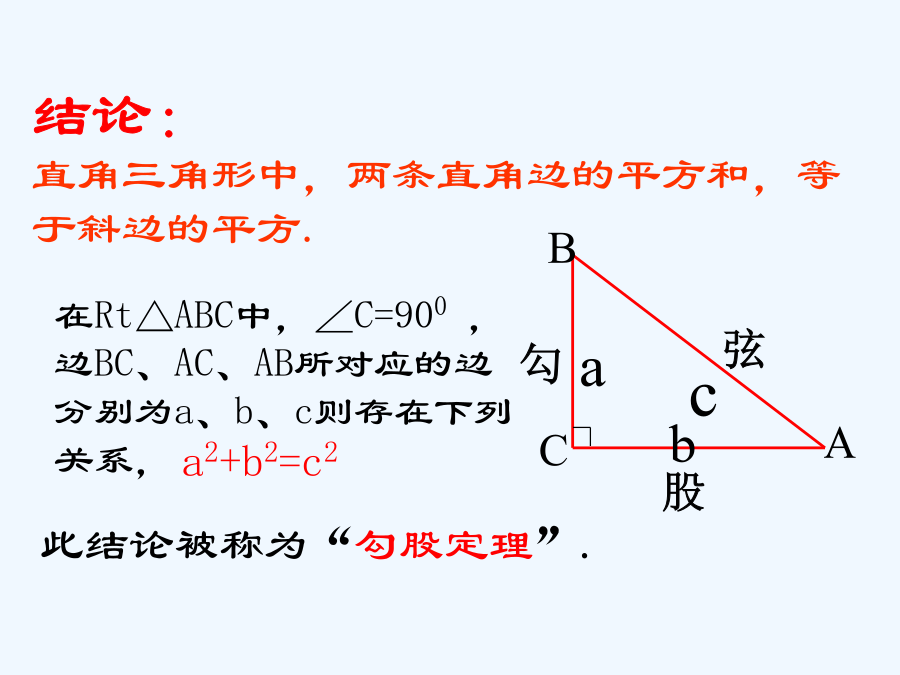
历史因你而改变学习因你而精彩情境引入情境引入数学家毕达哥拉斯的发现：课中探究尝试应用此结论被称为“勾股定理”.如果直角三角形的两直角边分别为a，b，斜边为c，那么尝试应用勾股定理的运用已知直角三角形的任意两条边长，求第三条边长.例2：将长为5米的梯子AC斜靠在墙上，BC长为2米，求梯子上端A到墙的底端B的距离.求下列图中表示边的未知数x、y、z的值.1、直角ABC的两直角边a=5,b=12,c=_____2、直角ABC的一条直角边a=10,斜边c=26，则b=().３、已知：∠C＝90°，a=6，a：
2024-11-07
10
383KB
八下171勾股定理(第1课时)课件.ppt
历史因你而改变学习因你而精彩情境引入情境引入数学家毕达哥拉斯的发现：课中探究尝试应用此结论被称为“勾股定理”.如果直角三角形的两直角边分别为a，b，斜边为c，那么尝试应用勾股定理的运用已知直角三角形的任意两条边长，求第三条边长.例2：将长为5米的梯子AC斜靠在墙上，BC长为2米，求梯子上端A到墙的底端B的距离.求下列图中表示边的未知数x、y、z的值.1、直角ABC的两直角边a=5,b=12,c=_____2、直角ABC的一条直角边a=10,斜边c=26，则b=().３、已知：∠C＝90°，a=6，a：
2024-07-23
10
582KB
八下171勾股定理(第2课时).ppt
历史因你而改变学习因你而精彩勾股定理：直角三角形两直角边的平方和等于斜边的平方．结论变形（1）求出下列直角三角形中未知的边．（2）在长方形ABCD中，宽AB为1m，长BC为2m，求AC长．有一个边长为50dm的正方形洞口，想用一个圆盖去盖住这个洞口，圆的直径至少多长？（结果保留整数）课中探究变式练习:如图，一个3米长的梯子AB，斜着靠在竖直的墙AO上，这时AO的距离为2.5米．尝试应用2：如图，铁路上A，B两点相距25km，C，D为两庄，DA⊥AB于A，CB⊥AB于B，已知DA=15km,CB=10km，
2024-11-04
10
396KB
171勾股定理（第1课时）.ppt
第十七章勾股定理数学家曾建议用这个图作为与“外星人”联系的信号.这个图案有什么意义？温故知新拼图游戏2.请你计算这三个正方形的面积，它们之间存在什么数量关系？能否用一个等式表示出来？3．由上面的条件可知，这三个正方形的边长分别是1、1和2，那么刚才的面积关系可以用一个等量关系式来描述吗？请你写出这个等式.提问：进一步思考（1）观察右边两幅图：（3）你是怎样得到正方形C的面积的？“拼”的方法（1）观察右边两幅图：（1）你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗？直角三角形的两条直
2024-06-04
10
2MB
171勾股定理(第1课时).ppt
17.1.1这就是本届大会会徽的图案．读一读我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦.图1-1称为“弦图”，最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.漂亮的勾股树活动2数学家毕达哥拉斯的发现：活动3赵爽弦图的证法┏1.求下列图中表示边的未知数x、y、z的值.做一做：
2024-06-11
10
1.6MB