内容提供者
171勾股定理(第1课时).ppt
2024-06-11
10金币
1.6MB
23页
仙人****88
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
亲，该文档总共23页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
171第1课时勾股定理.ppt
据说我国著名的数学家华罗庚曾建议“发射”一种勾股定理的图形(如图).勾股定理有着悠久的历史：古巴比伦人和古代中国人看出了这个关系，古希腊的毕达哥拉斯学派首先证明了这关系，下面让我们一起来通过视频来了解吧：讲授新课问题3在网格中一般的直角三角形，以它的三边为边长的三个正方形A、B、C是否也有类似的面积关系？观察下边两幅图(每个小正方形的面积为单位1)：方法1：补形法(把以斜边为边长的正方形补成各边都在网格线上的正方形）：方法2：分割法(把以斜边为边长的正方形分割成易求出面积的三角形和四边形）：根据前面求出的
2024-06-11
10
4MB
171勾股定理(第1课时).ppt
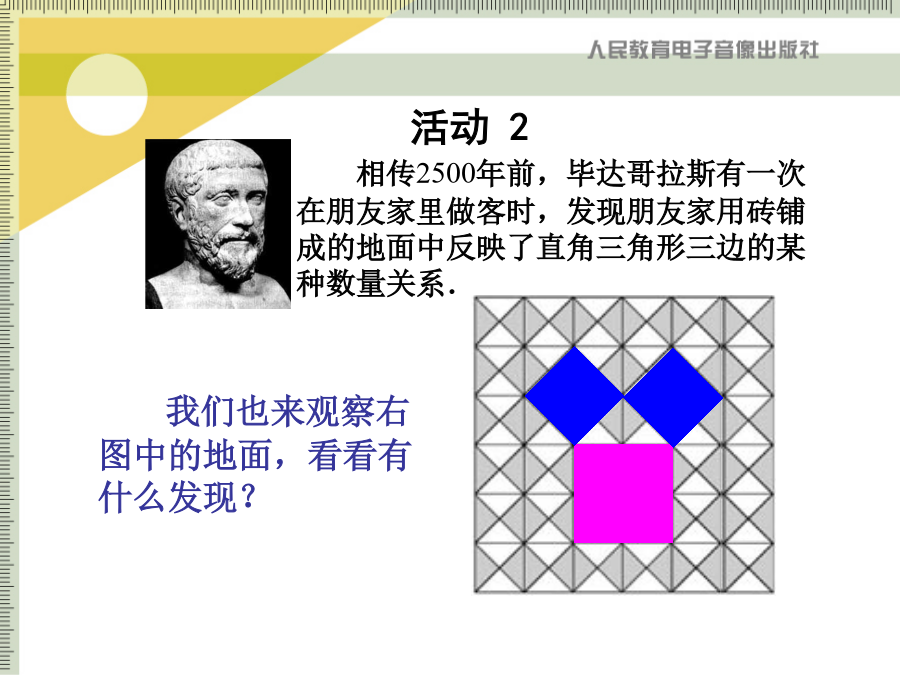
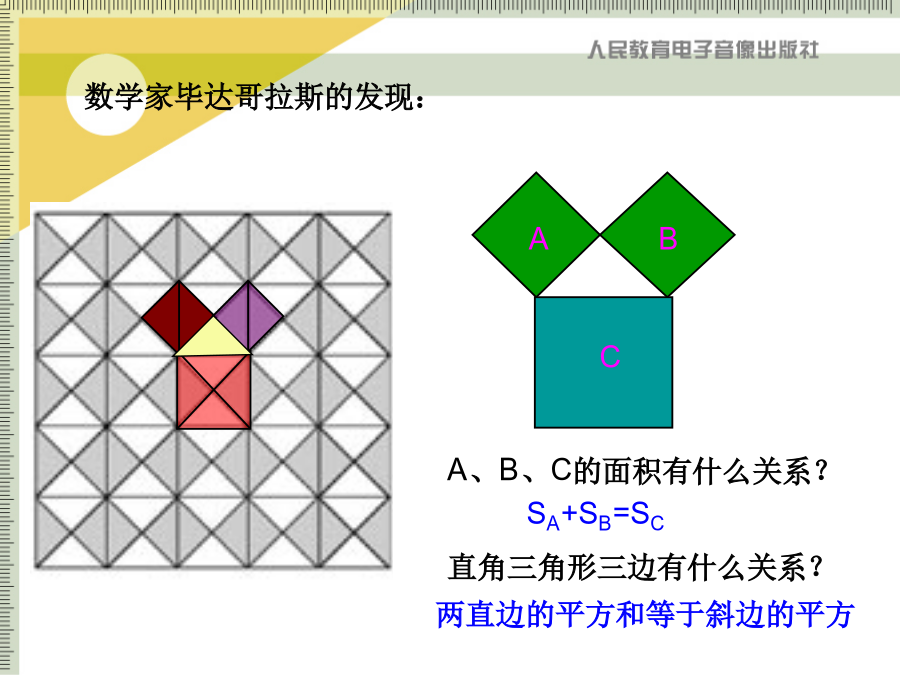
17.1.1这就是本届大会会徽的图案．读一读我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦.图1-1称为“弦图”，最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.漂亮的勾股树活动2数学家毕达哥拉斯的发现：活动3赵爽弦图的证法┏1.求下列图中表示边的未知数x、y、z的值.做一做：
2024-06-11
10
1.6MB
171勾股定理第1课时.doc
人教八年级下册第17章17.1勾股定理第1课时章节八下第17章课题17.1勾股定理第1课时课程类型新授课教学目标目标解读1.经历探索勾股定理的过程,体会数形结合和从特殊到一般的思想.2.会用面积法证明勾股定理,会应用勾股定理进行简单的计算.重点难点重点：勾股定理及其证明。难点：用多种方法证明勾股定理。导学建议学法指导直角三角形的三边关系，可变形为或。2.用不同的代数工表示同一图形面积的方法，是我们证明勾股定理的重要方法。教学建议在预习的第一环节中，重点引导两个结论：①在直角三角形中，以斜边为边长的正方形的
2024-06-10
10
480KB
171勾股定理(第1课时).ppt
第十七章勾股定理观察思考得出结论:以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.一起探究由上面的几个例子,我们得到猜想:经过证明被确认正确的命题叫定理.拓广应用解:连接AC.在Rt△ABC中,根据勾股定理,因此,因为AC大于木板的宽,所以木板能从门框内通过.2.练习练习3.如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m.你能求出A、B两点间的距离吗(结果保留整数)?反思与评价(1)由特殊例子的考察，经历在具体情境中观察
2024-06-15
10
1.2MB
171勾股定理（第1课时）.ppt
第十七章勾股定理数学家曾建议用这个图作为与“外星人”联系的信号.这个图案有什么意义？温故知新拼图游戏2.请你计算这三个正方形的面积，它们之间存在什么数量关系？能否用一个等式表示出来？3．由上面的条件可知，这三个正方形的边长分别是1、1和2，那么刚才的面积关系可以用一个等量关系式来描述吗？请你写出这个等式.提问：进一步思考（1）观察右边两幅图：（3）你是怎样得到正方形C的面积的？“拼”的方法（1）观察右边两幅图：（1）你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗？直角三角形的两条直
2024-06-15
10
2MB