
171勾股定理(第1课时).ppt

sy****28









亲,该文档总共36页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

171勾股定理第1课时.doc
人教八年级下册第17章17.1勾股定理第1课时章节八下第17章课题17.1勾股定理第1课时课程类型新授课教学目标目标解读1.经历探索勾股定理的过程,体会数形结合和从特殊到一般的思想.2.会用面积法证明勾股定理,会应用勾股定理进行简单的计算.重点难点重点:勾股定理及其证明。难点:用多种方法证明勾股定理。导学建议学法指导直角三角形的三边关系,可变形为或。2.用不同的代数工表示同一图形面积的方法,是我们证明勾股定理的重要方法。教学建议在预习的第一环节中,重点引导两个结论:①在直角三角形中,以斜边为边长的正方形的

171勾股定理(第1课时).ppt
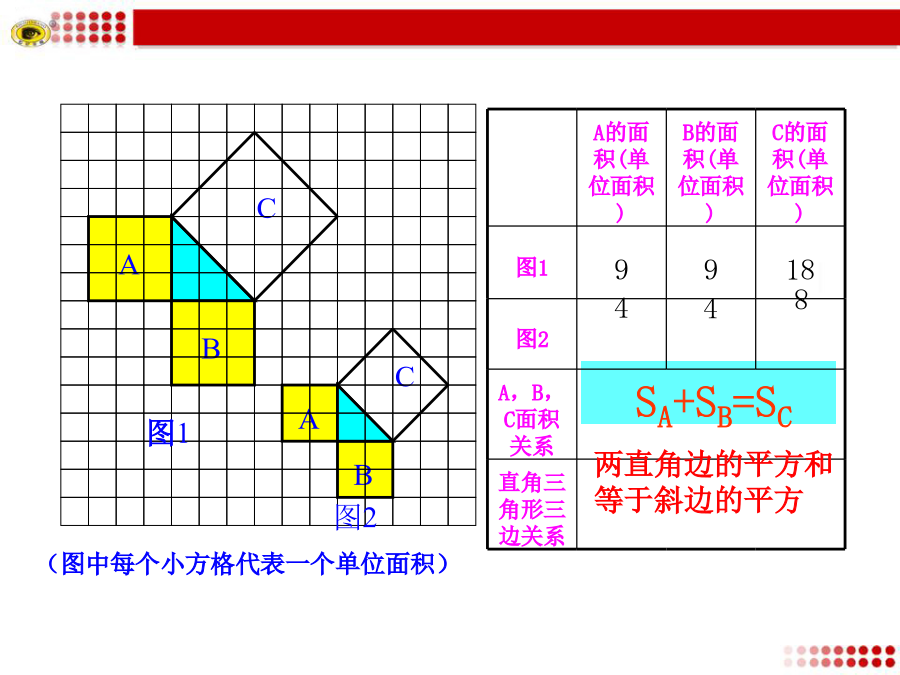
第十七章勾股定理数学家曾建议用这个图作为与“外星人”联系的信号.这个图案有什么意义?温故知新拼图游戏2.请你计算这三个正方形的面积,它们之间存在什么数量关系?能否用一个等式表示出来?3.由上面的条件可知,这三个正方形的边长分别是1、1和2,那么刚才的面积关系可以用一个等量关系式来描述吗?请你写出这个等式.提问:进一步思考(1)观察右边两幅图:(3)你是怎样得到正方形C的面积的?“拼”的方法(1)观察右边两幅图:(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?直角三角形的两条直

171勾股定理(第1课时).ppt
第十七章勾股定理17.1勾股定理(第1课时)1.掌握勾股定理的内容.2.理解勾股定理的证明.3.应用勾股定理进行有关计算与证明.星期日老师带领初二全体学生去凌峰山风景区游玩,同学们看到山势险峻,查看景区示意图得知:凌峰山主峰高约为900米,如图:为了方便游人,此景区从主峰A处向地面B处架了一条缆车路线,已知山底端C处与地面B处相距1200米,,请问缆车路线AB长应为多少?读一读我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由汉代的数学家赵爽在为《周髀

171勾股定理(第1课时).ppt
第十七章勾股定理17.1勾股定理(第1课时)1.掌握勾股定理的内容.2.理解勾股定理的证明.3.应用勾股定理进行有关计算与证明.星期日老师带领初二全体学生去凌峰山风景区游玩,同学们看到山势险峻,查看景区示意图得知:凌峰山主峰高约为900米,如图:为了方便游人,此景区从主峰A处向地面B处架了一条缆车路线,已知山底端C处与地面B处相距1200米,,请问缆车路线AB长应为多少?读一读我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由汉代的数学家赵爽在为《周髀

171勾股定理(第1课时).ppt
第十七章勾股定理数学家曾建议用这个图作为与“外星人”联系的信号.这个图案有什么意义?温故知新拼图游戏2.请你计算这三个正方形的面积,它们之间存在什么数量关系?能否用一个等式表示出来?3.由上面的条件可知,这三个正方形的边长分别是1、1和2,那么刚才的面积关系可以用一个等量关系式来描述吗?请你写出这个等式.提问:进一步思考(1)观察右边两幅图:(3)你是怎样得到正方形C的面积的?“拼”的方法(1)观察右边两幅图:(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?直角三角形的两条直
