高一必修五余弦定理(一)-PPT.ppt

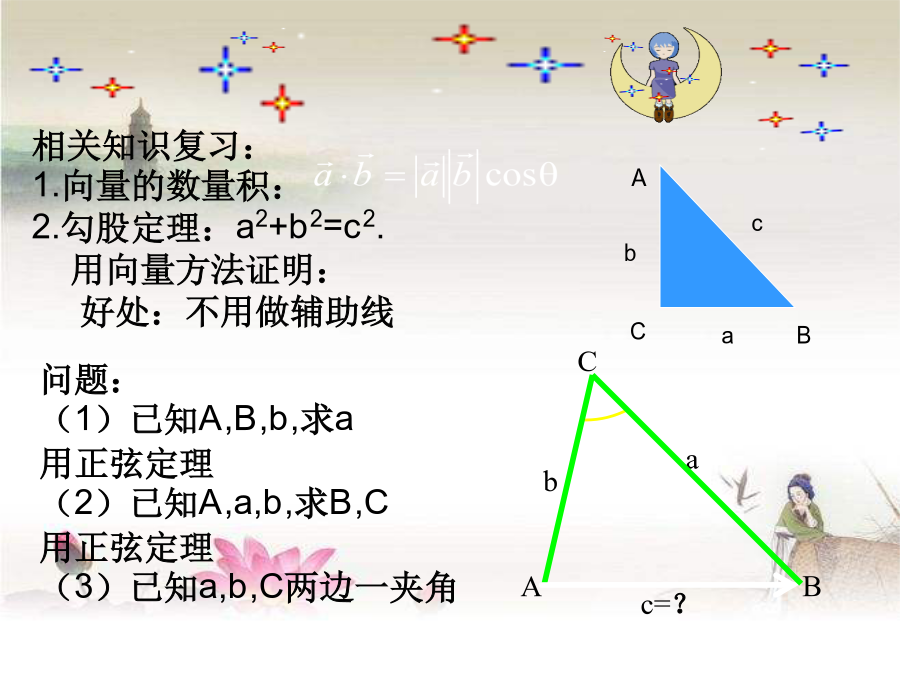
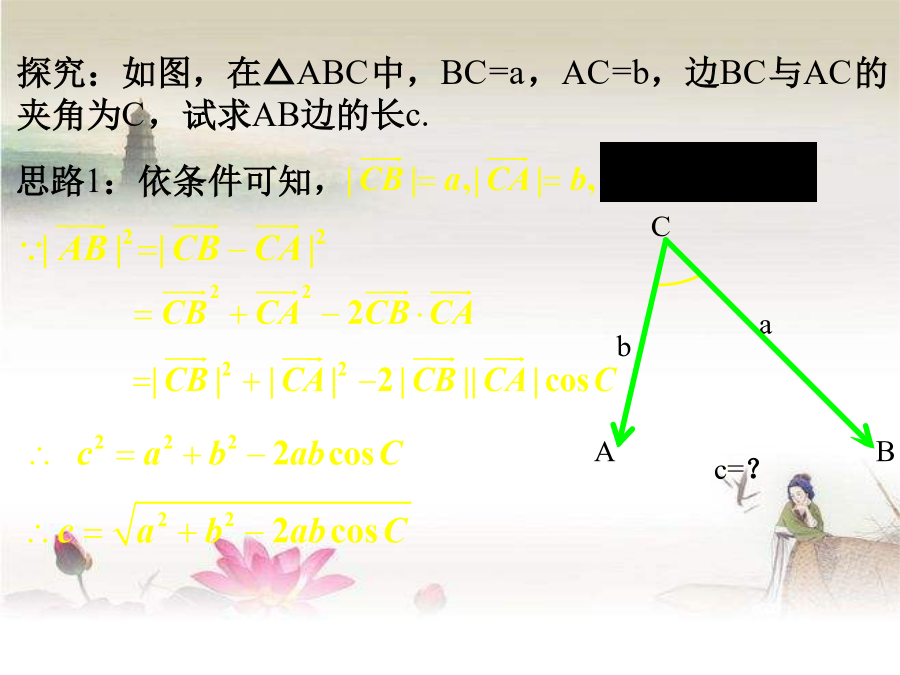
1.1.2、余弦定理复习
一、正弦定理可解决两类三角问题：
1、知两角及一边，求其它的边和角；
2、知两边及其中一边的对角，求其它的边和角.相关知识复习：
1.向量的数量积：
2.勾股定理：a2+b2=c2.
用向量方法证明：
好处：不用做辅助线确定三角形方法？
ASA,
AAS,
SAS,
SSSAA如图所示建立直角坐标系，点A，B的坐标分别是什么？
根据两点间的距离公式可得什么结论？1.1.2、余弦定理三角形任何一边的平方等于其他两边的平方和
减去这两边与它们夹角的余弦的积的两倍，即例1、在△ABC中，已知b=60cm，c=34cm，A=41o，
解该三角形（角度精确到1°，边长精确到1cm）.例2、在△ABC中，已知a=134.6cm，b=87.8cm，
c=161.7cm，解三角形（角度精确到1′）。利用余弦定理，可以解决以下两类解三角形的问题：
（1）已知两边及其夹角，求其它的边和角；
（2）已知三边，求三个角.在△ABC中,若a=5、b=7、c=9，判断△ABC是锐角三角形还是钝角三角形.在三角形的六个基本元素中，已知哪三个元素可以解三角形？例3、已知在△ABC中，a=8，b=7，B=60o，求c.（1）知两角及一边
先求第三角，再用正弦定理求另外两边.
（2）知两边及其中一边的对角：
①先用正弦定理求剩下两角，再求第三边；
②先用余弦定理求第三边，再求剩下两角.
（3）知两边及其夹角
先用余弦定理求第三边，再求剩下两角.
（4）知三边
用余弦定理求三个角.结合正弦定理， 可作什么变形？1、在△ABC中，已知a=，c=cm，B=45o，
解三角形（保留根号）.