统计学07抽样推断.pptx

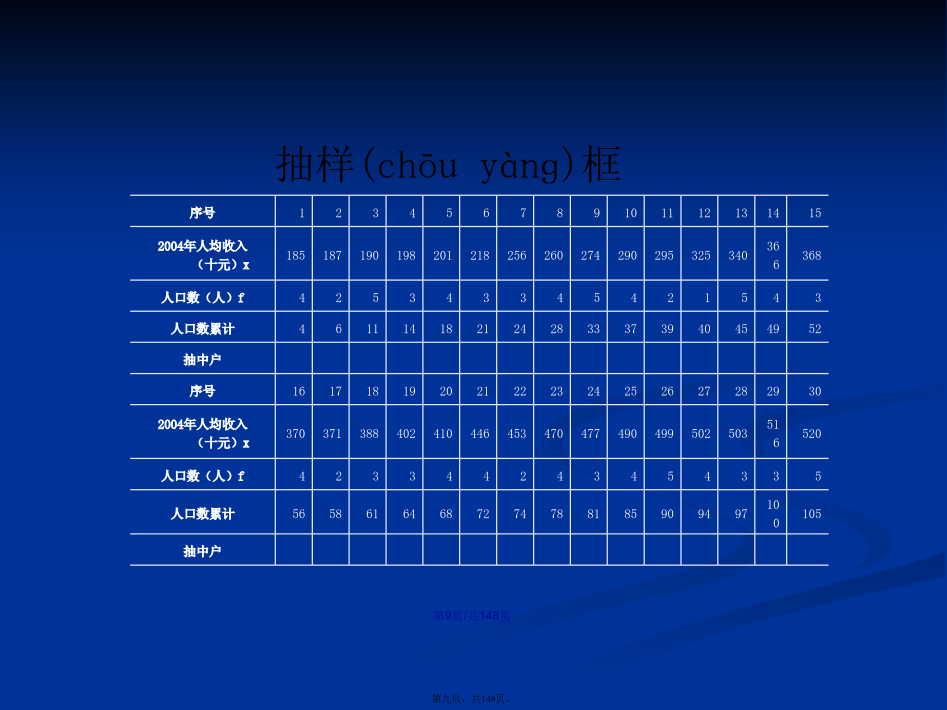
会计学几个(jǐɡè)基本概念7.1抽样推断(tuīduàn)概述7.1抽样推断(tuīduàn)概述7.1抽样(chōuyànɡ)推断概述：抽样(chōuyànɡ)的组织方式3.等距抽样的：
亦叫机械抽样
先将总体(zǒngtǐ)各单位按某一标志排队
然后按等距离抽取样本单位等距抽样(chōuyànɡ)的操作程序：
第一步：编制抽样(chōuyànɡ)框
将全及总体按有关标志（x）从低到高顺序排队
列出辅助标志（f）
将辅助标志依次累计例序号第二步：计算(jìsuàn)抽样距离（K）第三步：抽取调查(diàochá)单位半距起点(qǐdiǎn)、等距抽样以抽取(chōuqǔ)6户为例，抽取(chōuqǔ)的户数依次为：第四步：对抽中单位(dānwèi)进行代表性检查现以半距起点(qǐdiǎn)、等距抽取的6户为例，检查其代表性4、整群抽样(chōuyànɡ)7.1抽样(chōuyànɡ)推断概述：抽样(chōuyànɡ)的组织方式7.1抽样推断(tuīduàn)概述：抽样方法7.2抽样分布(fēnbù)及抽样推断理论依据 ——基础知识7.2抽样分布及抽样推断(tuīduàn)理论依据 ——基础知识：概率7.2抽样(chōuyànɡ)分布及抽样(chōuyànɡ)推断理论依据 ——基础知识：概率7.2抽样分布及抽样推断(tuīduàn)理论依据 ——基础知识：随机变量7.2抽样分布(fēnbù)及抽样推断理论依据 ——基础知识：概率分布(fēnbù)7.2抽样分布(fēnbù)及抽样推断理论依据 ——基础知识：正态分布(fēnbù)7.2抽样(chōuyànɡ)分布及抽样(chōuyànɡ)推断理论依据 ——基础知识：正态分布7.2抽样(chōuyànɡ)分布及抽样(chōuyànɡ)推断理论依据 ——基础知识：正态分布7.2抽样(chōuyànɡ)分布及抽样(chōuyànɡ)推断理论依据 ——基础知识：正态分布两条正态分布的密度曲线(qūxiàn)。左边是N(-2,0.5)分布，右边是N(0,1)分布正态分布标准正态变量在区间(qūjiān)(0.51,1.57)中的概率7.2抽样分布(fēnbù)及抽样推断理论依据 ——基础知识：参数与统计量7.2抽样(chōuyànɡ)分布及抽样(chōuyànɡ)推断理论依据 ——P200三种分布所有样本指标（如均值、成数、方差等）所形成的分布称为(chēnɡwéi)抽样分布
是一种理论概率分布
随机变量是样本统计量
样本均值,样本成数等
结果来自容量相同的所有可能样本 样本均值的抽样(chōuyànɡ)分布（一个例子）样本均值的抽样(chōuyànɡ)分布（一个例子）样本均值的抽样分布（一个(yīɡè)例子）所有(suǒyǒu)样本均值的均值和方差样本均值的分布与总体(zǒngtǐ)分布的比较7.2抽样分布及抽样推断(tuīduàn)理论依据 ——大数定律样本均值的抽样分布(fēnbù)与中心极限定理中心(zhōngxīn)极限定理1.抽样调查的主要目的在于（）。
计算和控制误差B.了解(liǎojiě)总体单位情况
Ｃ.用样本来推断总体
D.对调查单位作深入的研究

2.抽样调查所必须遵循的基本原则是（）。
随意原则B.可比性原则Ｃ.准确性原则D.随机原则

3.在下列情况下，计算不重复抽样的抽样平均误差可以采用重复抽样公式（）。
A.总体单位数很多B.抽样单位数很少
Ｃ.抽样单位数对总体单位数的比重很小；
D.抽样单位数对总体单位数的比重较大。7.4参数估计7.4.1抽样误差的概念(gàiniàn)理解抽样误差可以(kěyǐ)从两方面着手：误差(wùchā)样本统计量抽样平均误差是反映抽样误差一般水平(shuǐpíng)的指
标，其实质是指抽样平均数的标准差，它反
映了是指样本指标与总体指标的平均离差程
度，也就是样本指标与总体指标的标准差，
通常用来表示。
可以作为衡量样本指标对于(duìyú)全及指标代表性程度的一个尺度。
是计算样本指标与全及指标之间变异范围的一个根据。
在组织抽样调查中，也是确定抽样单位数多少的计算依据之一。7.1.2影响(yǐngxiǎng)抽样平均误差的因素1.重复抽样(chōuyànɡ)的条件下2.不重复(chóngfù)抽样的条件下抽样(chōuyànɡ)平均数的平均误差例题：解：先列表(lièbiǎo)计算(jìsuàn)平均数即平均工资：抽样(chōuyànɡ)成数的平均误差例题：练习：要估计某高校10000名在校生的近视率，现随机从中抽取400名，检查(jiǎnchá)有近视眼的学生320名，试计算样本近视率的抽样平均误差。
解：根据已知条件：2）在不重复(chóngfù)抽样条件下，
样本近视率的抽样平均误差：7.1.4抽样极限(jíxi