内容提供者
平稳随机过程.ppt
2024-10-01
10金币
5.4MB
88页
lj****88
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
亲，该文档总共88页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
平稳随机过程.ppt
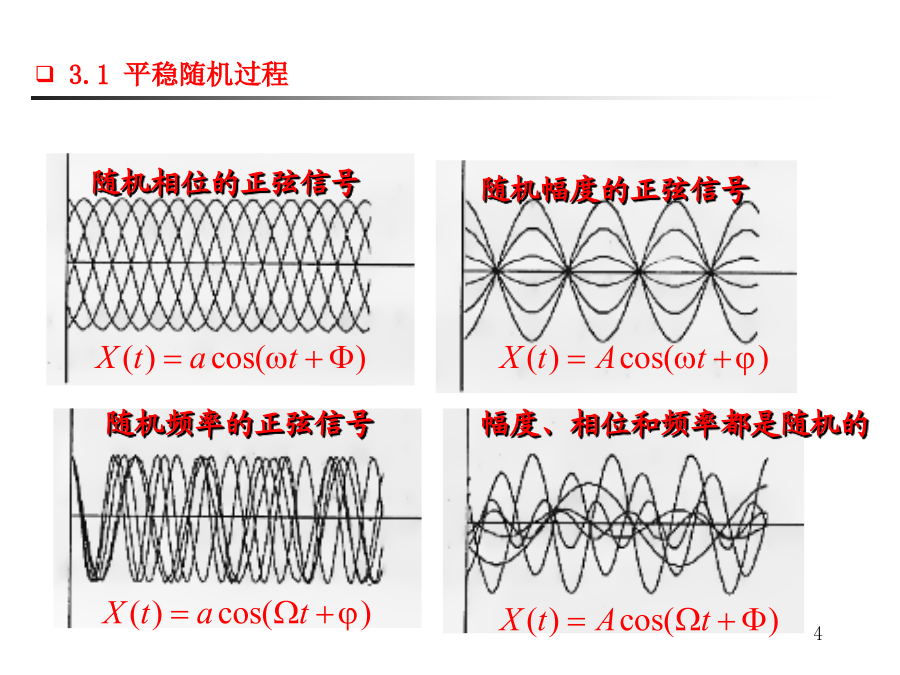
12343.1平稳随机过程789102、严平稳过程X(t)的二维概率密度只与两个时刻t1和t2的间隔有关，与时间起点无关。一维概率密度与时间有关，故不是严平稳过程。一个严平稳过程只要它的均方值有限，则它必定是广义平稳的。但是，反之则不一定成立。随机幅度的正弦信号3.1平稳随机过程3.1平稳随机过程3.1平稳随机过程3.1平稳随机过程3.1平稳随机过程3.1平稳随机过程3.1平稳随机过程3.1平稳随机过程3.1平稳随机过程3.1平稳随机过程253.1平稳随机过程27283.1平稳随机过程3.1平稳随机过程3
2024-10-01
10
5.4MB
三平稳随机过程.pptx
三平稳随机过程平稳随机过程得概念(1)定义(2)一、二维概率密度及数学特征严平稳随机过程得二维概率密度只与t1,t2得时间间隔有关,而与时间起点无关例1、设随机过程Z(t)=Xsint+Ycost,其中X和Y是相互独立得二元随机变量,它们都分别以2/3和1/3得概率取-1和2,试求:Z(t)得均值和自相关函数;证明Z(t)是宽平稳得,但不是严平稳得。12因此,Z(t)不是严平稳得。例2、设随机过程X(t)=t2+Asint+Bcost,其中A和B都是一元随机变量,且E[A]=E[B]=0,D[A]=D[B
2024-09-10
10
1.7MB
窄带平稳随机过程.ppt
窄带平稳随机过程窄带平稳随机过程的表示窄带平稳随机过程的性质窄带随机过程性质（证）白噪声窄带平稳高斯过程窄带平稳高斯过程（零均值）窄带平稳高斯过程（零均值）证明|J|为Jacobian行列式因此则结论余弦波加窄带高斯平稳过程证明其中，I0(x)称为零阶修正贝塞尔函数(Bessel)循环平稳过程循环平稳过程的统计特性
2024-09-11
10
210KB
非平稳随机过程.pptx
1单整的定义随机游走过程AR(1)过程单积过程的统计特征—以随机游走过程和平稳的AR(1)过程作比较AR(1)过程随机游走过程和平稳的AR(1)过程的对比图示T=50、100、500、1000条件下随机游走过程对应的自相关函数图（rho1000=(1-(@trend(0)/1000))^.5）AR(1)过程自相关系数1与方差的关系虚假相关两个相互独立的I(0)变量{ut}和{vt}的相关系数Ruv的分布为正态（见图）两个相互独立的I(1)变量的相关系数的分布两个相互独立的I(2)变量的相关系数的分布虚假
2024-09-19
20
1.4MB
随机过程-2-平稳过程.pptx
随机过程-2-平稳过程.pptx§1平稳过程概念连续一维二维与t无关，一元函数定义：设的一、二阶矩存在，若与t无关，则称之为弱（宽、广义）平稳（随机）过程。一般地强～弱～二阶矩过程强～弱～定理：正态过程弱平稳强平稳下面均讨论弱平稳随机过程例1随机序列，X(n)两两不相关，例2随机序列，X(n)两两不相关，N为自然数，为常数。称为离散白噪声的滑动和。推广：且收敛。称为离散白噪声的无限滑动和。例3，为正常数，判断是否弱平稳。例4，为正常数，A,B独立，判断是否弱平稳。例5，X(t)只取，内正负号变化次数记为，
2024-06-30
10
6MB