翼型气动特性.pptx

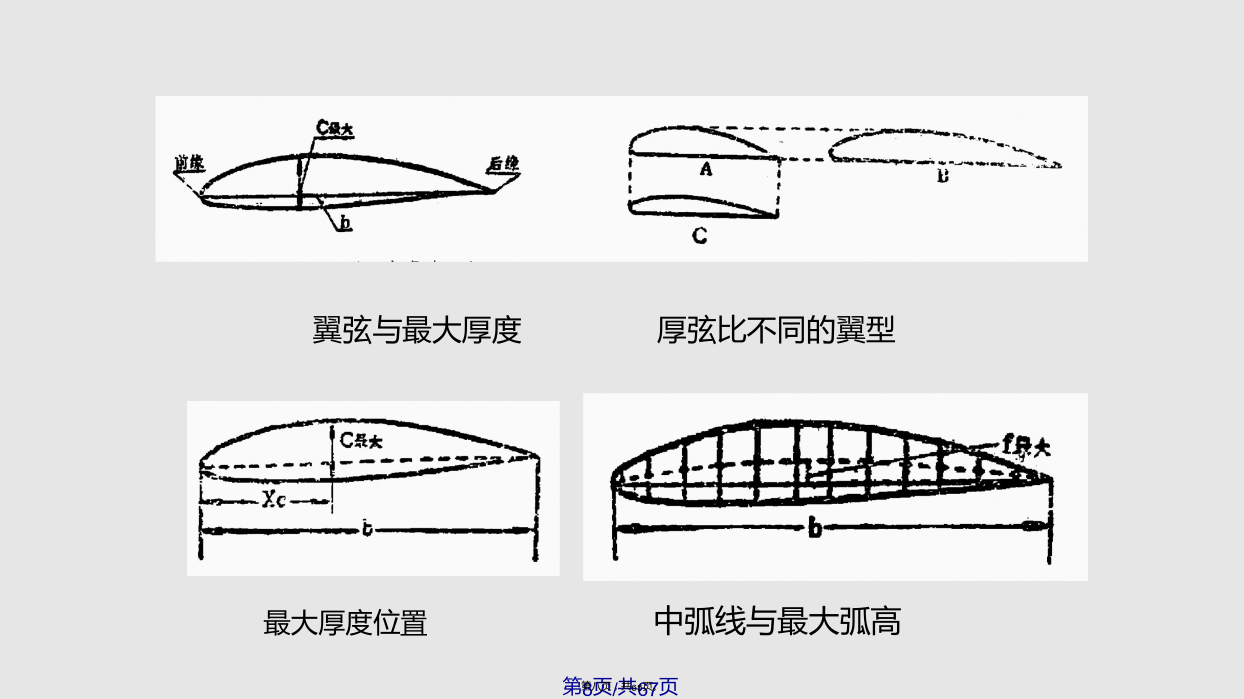
引言引言§5.1翼型的几何参数
§5.2翼型空气动力系数
§5.3低速翼型的流动特点及起动涡
§5.4库塔—儒可夫斯基后缘条件和
环量确定
§5.5薄翼型理论
§5.6任意翼型位流解法
§5.7低速翼型的一般气动特性翼弦与最大厚度厚弦比不同的翼型§5.2翼型空气动力系数§5.2.1翼型的迎角和空气动力翼剖面§5.2.1翼型的迎角和空气动力§5.2.1翼型的迎角和空气动力§5.2.2翼型的空气动力系数§5.2.2翼型的空气动力系数§5.2.3压力中心§5.2.3压力中心§5.2.3压力中心(a)00迎角绕流(c)150迎角绕流(a)小迎角无分离(b)厚翼型后缘分离(c)薄翼型前缘分离§5.3低速翼型的流动特点及起动涡§5.3低速翼型的流动特点及起动涡后缘绕流在上翼面出现分离，产生逆时针旋涡，后驻点O1移向后缘点B后驻点O1移至后缘点B时，后缘绕流分离形成的涡脱离翼面流向下游，
形成起动涡，后缘处上下翼面流动平顺汇合流向下游。由于远离翼面处流动不受粘性影响，所以
Γ=0
若设边界层和尾流中的环量为Γ3，则应有
Γ=Γ1+Γ2+Γ3
于是
Γ1=-（Γ2+Γ3）
此时，如不计粘性影响，绕翼型的速度环量与起动涡的速度环量大小相等、方向相反，即

Γ1=-Γ2
绕翼型无粘位流的升力问题，遵循儒可夫斯基升力定理。根据该定理，直均流流过任意截面形状翼型的升力：
Y=ρV∞Γ
可见，确定速度环量是关键。在第三章中，给出了定常、无粘、不可压流绕圆柱的流动。值得注意的是，绕圆柱的速度环量是任意给定的；不过，这个例子给出重要的一点：绕圆柱的速度环量值不同，圆柱面上驻点的位置就不同，两者一一对应；换言之，若指定驻点在圆柱上的位置，就只有唯一的速度环量值与之相对应。

在绕翼型无粘位流中，也有这种情况：对于形状一定的翼型而言，在给定来流密度、速度及迎角条件下，绕翼型的速度环量可以有多个值，均满足翼型表面为流线的边界条件，但环量值不同，后驻点在翼面上的位置不同。就无粘位流而言，给定来流流速、迎角和翼型时，下面
三种绕流情形都是可能的：
(a)后驻点在上翼面，有逆时针后缘绕流；
(b)后驻点在下翼面，有顺时针后缘绕流；
(c)后驻点在后缘，无后缘绕流。后驻点在翼面上而不在后缘时，绕尖后缘的流动流速理论上无穷大、压强负无穷，物理上这是不可能的；只有后驻点在后缘，不出现尖后缘绕流，上下翼面流动在后缘平顺汇合流向下游,后缘处流速为有限值，才合乎一般的物理要求。此时,有唯一的速度环量值与之相对应。确定了无粘位流理论涉及的速度环量的唯一性，这是库塔—儒可夫斯基后缘条件的实质。翼型低速无粘位流问题，一般可描述如下：翼型绕流速度位Φ满足拉普拉斯方程，因此它可分解为
直均来流速度位φ∞和翼型存在引起的扰动速度位φ，
即体轴坐标系因翼型薄，弯度和迎角小，即视为一阶小量，则为二阶小量；根据伯努利方程，流场中任一点的压强系数为，——扰动速度位的线性叠加（续）图迎角—弯板的面涡模拟面涡强度γ(ξ)的三角级数解升力问题的解面源及其基本特性面源及其基本特性面源及其基本特性解法：薄翼型的厚度问题，可在其弦线上布面源的方法求解。面源法大意面源法示例于是在第i控制点处的边界条件为翼面压强分布不仅是结构设计和强度计算的主要外载荷依据，也可用来判断翼型绕流
流态和近似确定升力和力矩特性。升力特性通常用升力曲线Cy-表示。升力特性中，升力线斜率、零升迎角和最大升力系数是三个基本参数。零升迎角零升迎角是零升力线与弦线的夹角，正弯度时是一个小负数。
理论和实验均表明，它主要与弯度大小有关，可用薄翼理论估算。最大升力系数最大升力系数与附面层的
分离密切相关，因此翼表面光洁度和雷诺数
对它有明显影响。常用低速翼型的最大升力
系数之约为1.3至1.7，随雷诺数的增大而增
大，一般由实验提供，见右图。力矩特性通常用曲线mz-Cy或mz1/4-Cy表示。
理论和实验均表明，在迎角或升力系数不太
大时，曲线mz-Cy接近一条直线，即翼型的压心和焦点低速时，翼型的阻力由粘性引起，分为两部分：
由翼面粘性切应力造成的摩擦阻力，及由附面层存在改变位流压强分布引起的压差阻力。感谢您的观看！内容总结