
一种基于H型精密运动平台的轮廓误差估计方法.pdf

宛菡****魔王









亲,该文档总共11页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

一种基于H型精密运动平台的轮廓误差估计方法.pdf
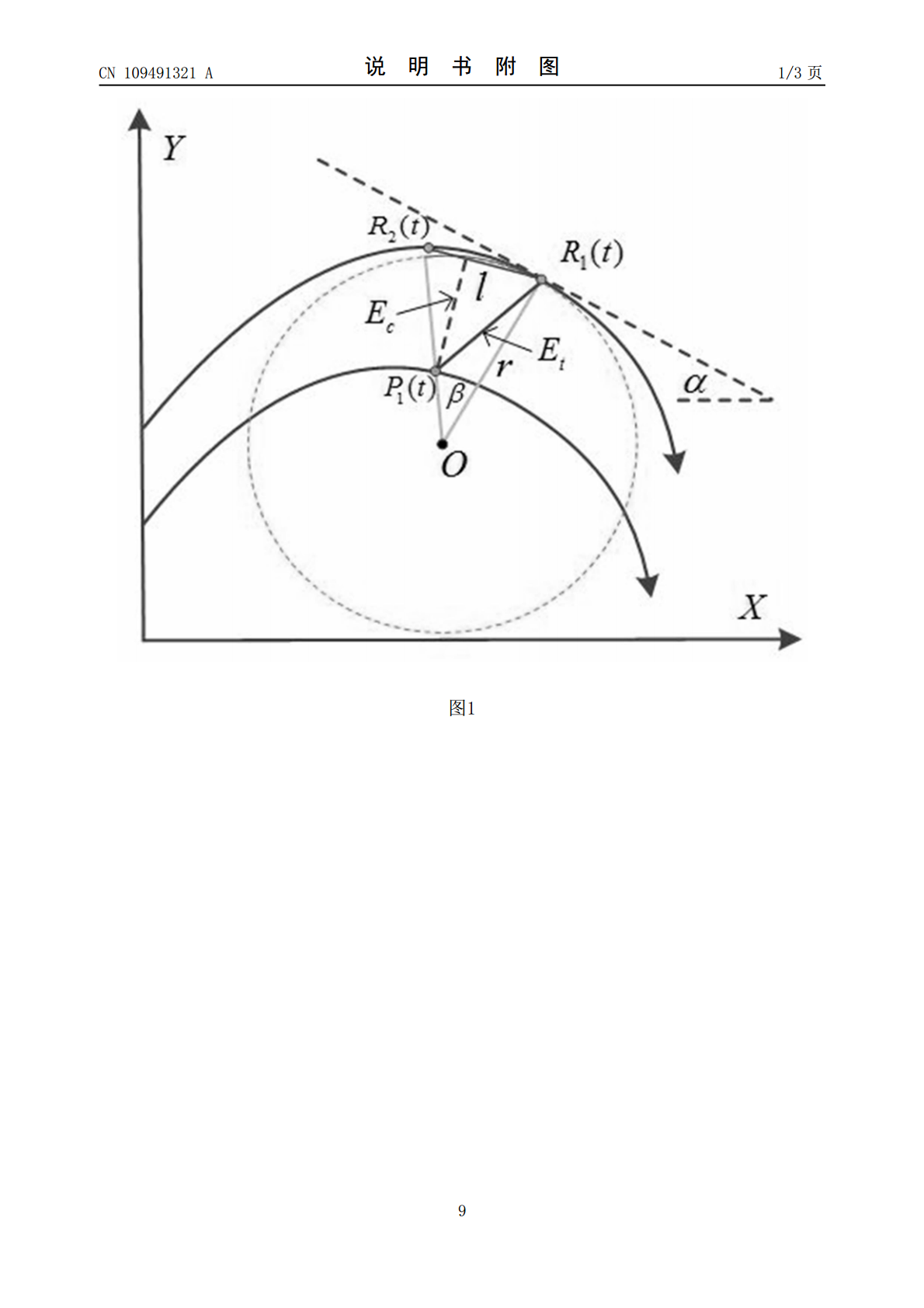
本发明属于精密高效数控加工技术领域,其对于不同曲率变化的自由曲线均可有效提升轮廓误差估计的准确度,进而降低轮廓跟踪运动中产生的轮廓误差。包括以下步骤:步骤一:计算H型精密运动平台期望加工轮廓上任意一参考点R

基于融合误差的直驱H型平台自适应全局滑模轮廓控制.docx
基于融合误差的直驱H型平台自适应全局滑模轮廓控制基于融合误差的直驱H型平台自适应全局滑模轮廓控制摘要:直驱H型平台是一种典型的并联机构,由于其非线性性质和不确定性的存在,控制难度较大。本文提出了一种基于融合误差的直驱H型平台自适应全局滑模轮廓控制方法,通过引入自适应全局滑模控制和轮廓控制两种技术,实现对直驱H型平台的精确控制。关键词:直驱H型平台;自适应控制;全局滑模控制;轮廓控制1.引言并联机构是机器人学和控制领域研究的热点之一,直驱H型平台作为一种重要的并联机构具有广泛的应用前景。然而,由于其动力学模

基于空间圆弧近似的轮廓误差实时估计方法.pdf
本发明基于空间圆弧近似的轮廓误差实时估计方法属于精密高效数控加工技术领域,涉及一种样条曲线插补过程中基于空间圆弧近似的轮廓误差实时估计方法。该方法在每步牛顿迭代计算垂足点前,基于一阶泰勒级数展开法计算参数曲线上用于牛顿迭代的参数初值,再利用牛顿迭代法,根据参数初值计算单步迭代参数终值。为避免大幅增加算法计算时间,根据迭代终止精度条件及最大迭代次数条件双重约束结束循环,得到垂足点参数估计值,计算轮廓误差矢量估计值。本方法在随动误差较大时仍可有效保证轮廓误差的估计精度,对提高高档数控机床样条曲线插补加工轮廓精

一种高精度实时轮廓误差估计方法.pdf
本发明一种高精度实时轮廓误差估计方法属于精密高效数控加工技术领域,涉及一种数控参数曲线插补加工过程中基于初值再生牛顿迭代法的高精度实时轮廓误差估计方法。该方法首先在每步迭代计算前,根据当前插补点参数和实际刀位点,基于一阶泰勒级数展开法计算参数曲线上用于牛顿迭代计算垂足点的迭代参数初值;其次,利用牛顿迭代法,根据迭代初值计算单步迭代参数终值;最后,为避免大幅增加算法计算时间,根据迭代终止条件及最大迭代次数条件双重约束结束迭代,得到垂足点参数估计值,进而计算轮廓误差矢量估计值。本发明可有效避免迭代发散、提高轮

一种基于置信域算法的多维空间轮廓误差估计方法.pdf
一种基于置信域算法的多维空间轮廓误差估计方法,本发明涉及基于置信域算法的多维空间轮廓误差估计方法。本发明为了解决现有多维空间轮廓误差补偿控制精度低及收敛性受初值影响大的缺点。本发明方法在每次迭代时求取当前迭代点的邻域作为迭代域,并在此邻域得到试探迭代步长,定义评价函数决定该步长的取舍及下一次迭代置信域范围,若该步长满足评价函数要求,则更新当前迭代状态并保持或扩大置信域,否则保持原迭代状态并减小置信域,直至精度满足要求或者迭代次数到达上限时停止迭代。相比于采用牛顿法,本发明方法保证了总体收敛性,减少了导数的
