一种基于置信域算法的多维空间轮廓误差估计方法.pdf

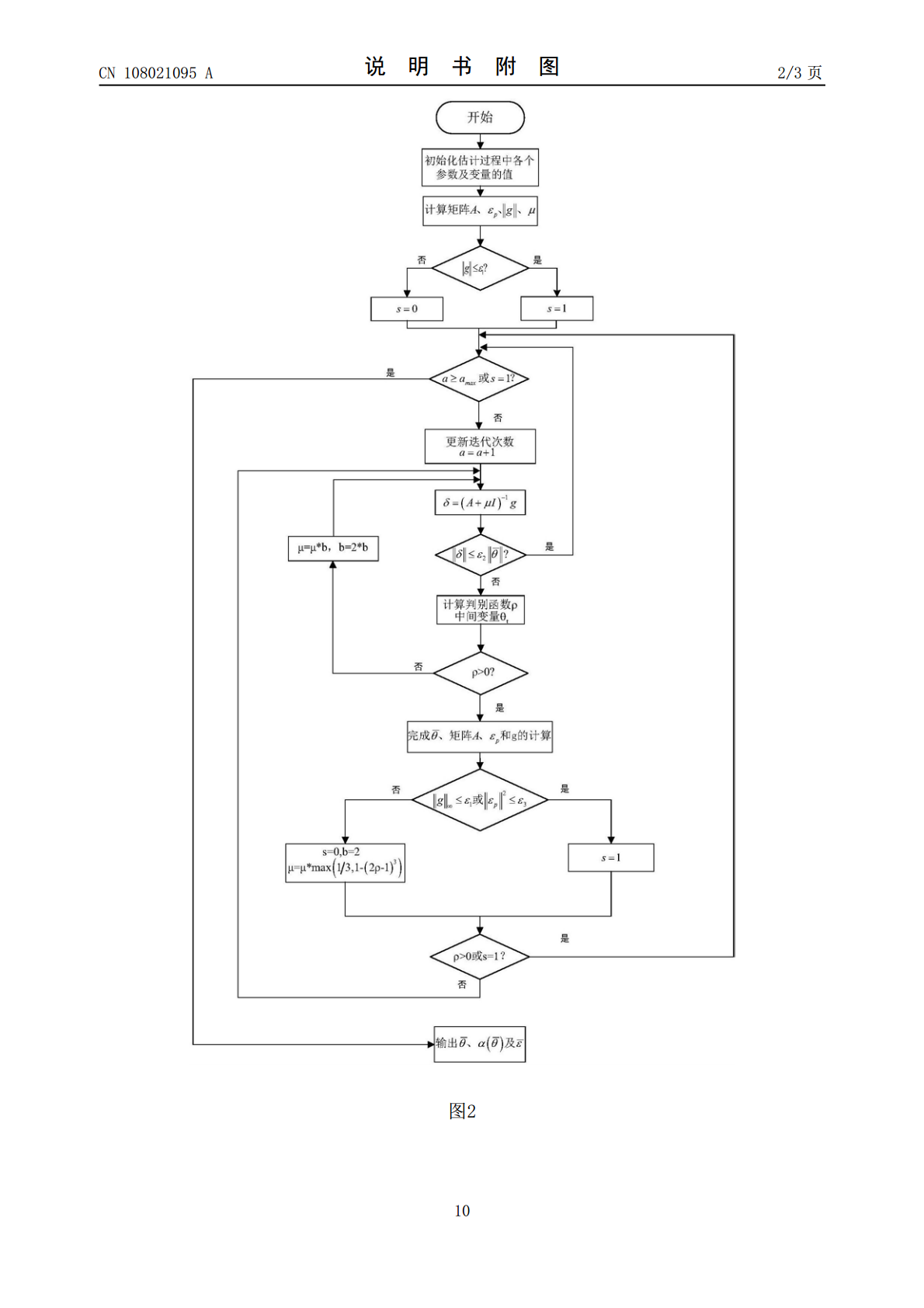
(19)中华人民共和国国家知识产权局(12)发明专利申请(10)申请公布号CN108021095A(43)申请公布日2018.05.11(21)申请号201711342106.X(22)申请日2017.12.14(71)申请人哈尔滨工业大学地址150001黑龙江省哈尔滨市南岗区西大直街92号(72)发明人孙光辉邵翔宇李晓磊匡治安吴承钰董瀚林(74)专利代理机构哈尔滨市松花江专利商标事务所23109代理人岳泉清(51)Int.Cl.G05B19/404(2006.01)权利要求书2页说明书5页附图3页(54)发明名称一种基于置信域算法的多维空间轮廓误差估计方法(57)摘要一种基于置信域算法的多维空间轮廓误差估计方法，本发明涉及基于置信域算法的多维空间轮廓误差估计方法。本发明为了解决现有多维空间轮廓误差补偿控制精度低及收敛性受初值影响大的缺点。本发明方法在每次迭代时求取当前迭代点的邻域作为迭代域，并在此邻域得到试探迭代步长，定义评价函数决定该步长的取舍及下一次迭代置信域范围，若该步长满足评价函数要求，则更新当前迭代状态并保持或扩大置信域，否则保持原迭代状态并减小置信域，直至精度满足要求或者迭代次数到达上限时停止迭代。相比于采用牛顿法，本发明方法保证了总体收敛性，减少了导数的求取。本发明用于轮廓跟踪及精密加工技术领域。CN108021095ACN108021095A权利要求书1/2页1.一种基于置信域算法的多维空间轮廓误差估计方法，其特征在于：所述基于置信域算法的多维空间轮廓误差估计方法包括以下步骤：步骤一：设置初始迭代次数a＝0以及停止迭代上限amax；初始化迭代增益系数b和阻尼增益系数τ；设定轮廓参数方程α(θ)中参数的初始估计值设置期望精度ε1＝ε2＝ε3，其中ε1表示估计误差εp的判别函数g的精度，ε2表示迭代过程中更新步长δ的精度，ε3表示估计误差εp的精度；转步骤二；步骤二：计算轮廓参数方程α(θ)的二阶微分矩阵的估计矩阵A＝JTJ，其中J为α(θ)的雅克比矩阵，JT为J的转置；计算当前采样时刻机床加工位置的估计误差p为当T前采样时刻机床加工的位置，为初始估计轮廓位置；计算判别函数g＝Jεp，并求取其Euclid范数||g||；求解初始阻尼系数μ＝τηmax(A)，其中ηmax(A)表示估计矩阵A中元素的最大值；转步骤三；步骤三：若||g||≤ε1,则s＝1，表示收敛到期望的精度值；否则s＝0，表示未收敛到期望的精度值。转步骤四；步骤四：若停止标志s＝1或迭代次数已经达到上限，即a≥amax，转步骤八，否则转步骤五；步骤五：更新迭代次数：a＝a+1，转步骤六；步骤六：由(A+μI)δ＝g求解更新步长δ及其Euclid范数||δ||，其中I为单位矩阵；若则s＝1；否则判别函数迭代过程的中间变量其中δT为δ的转置，为的Euclid范数；TT2若ρ＞0，则A＝JJ，g＝Jεp；若g的无穷范数||g||∞≤ε1或||εp||3≤ε3，则s＝1，否则s＝0，b＝2，μ＝μ*max(1/3,1-(2ρ-1))；若ρ≤0，则μ＝μ*b，b＝2*b，转步骤七；步骤七：若ρ＞0或s＝1，则转步骤四，否则转步骤八；步骤八：输出即为所估计出的状态值，即为所求解的轮廓上的位置，根据得到所估计的轮廓误差2.根据权利要求1所述的一种基于置信域算法的多维空间轮廓误差估计方法，其特征在于：所述步骤一中初始化迭代增益系数b＝2和阻尼增益系数τ＝10-3。3.根据权利要求2所述的一种基于置信域算法的多维空间轮廓误差估计方法，其特征-5在于：所述步骤一中设置期望精度ε1＝ε2＝ε3＝10。4.根据权利要求3所述的一种基于置信域算法的多维空间轮廓误差估计方法，其特征在于：所述步骤二中雅克比矩阵J具体为：其中为真实状态，为真实状态对应的轮廓。2CN108021095A权利要求书2/2页5.根据权利要求4所述的一种基于置信域算法的多维空间轮廓误差估计方法，其特征在于：所述步骤八中根据得到所估计的轮廓误差的具体为：3CN108021095A说明书1/5页一种基于置信域算法的多维空间轮廓误差估计方法技术领域[0001]本发明涉及基于置信域算法的多维空间轮廓误差估计方法。背景技术[0002]高速高精度的数控加工技术在工业生产中的地位越来越重要，因此提高数控加工过程的精度成了迫切需要解决的问题。基于轮廓误差跟踪的控制方法是提高加工精度的一种重要控制方法，这就需要对轮廓误差进行准确快速的估计，并根据估计的误差施加一定的控制作用，对系统进行控制。[0003]目前应用比较比广泛的动态轮廓误差估计方法主要是牛顿法，该方法根据初值计算单步迭代终值，但牛顿法是一种局部收敛的方法，其收敛性和初值的选取有关，并且在迭代过程中，牛顿法需要求取二阶偏导，会造成计算困难的情况。发明内容[000