
汽车减震器原理并.ppt

qw****27







亲,该文档总共15页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

汽车减震器原理并.ppt
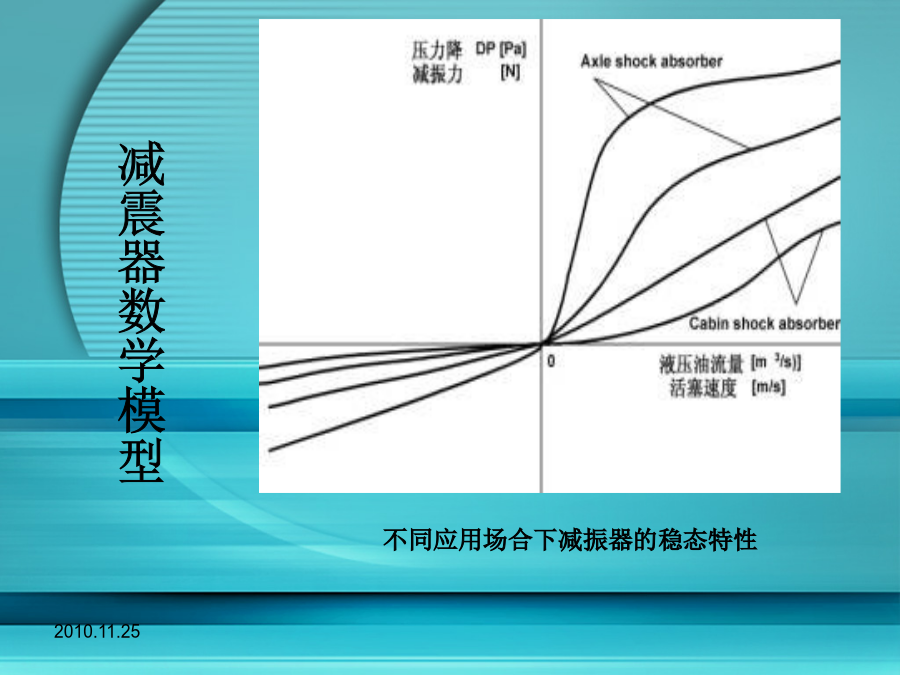
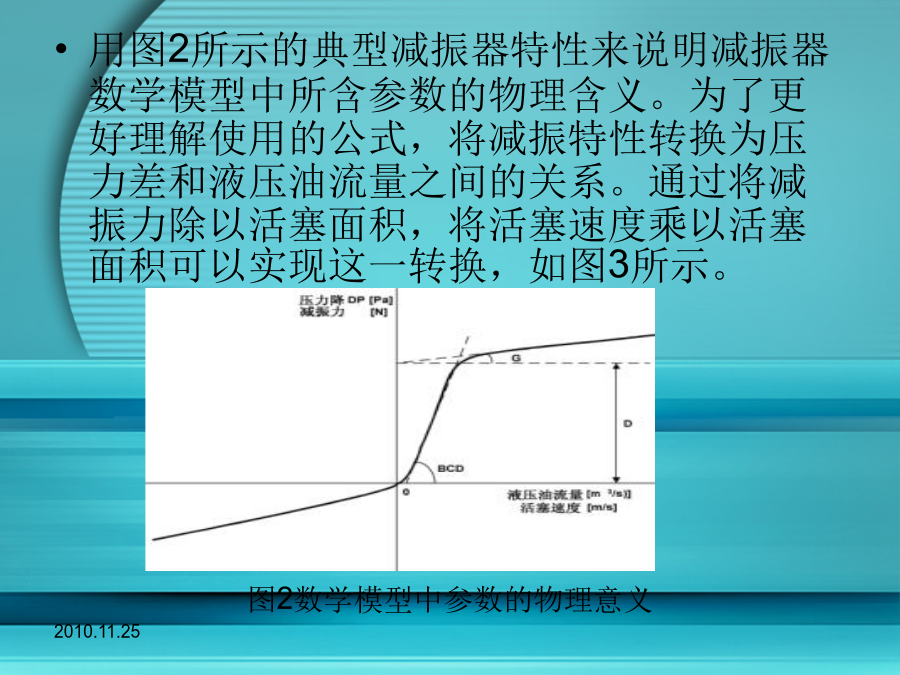
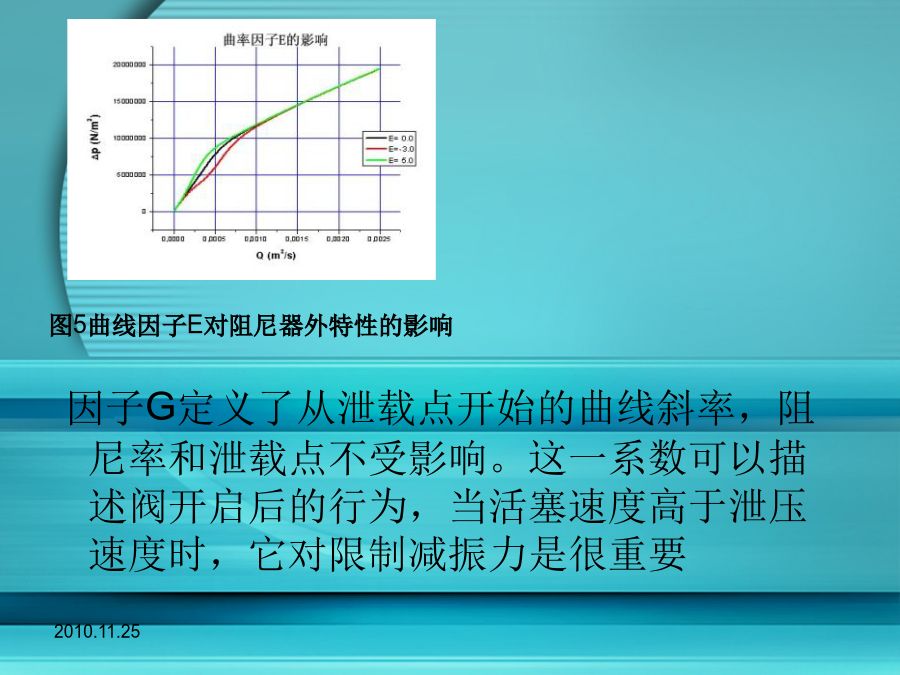
汽车减震器原理并建立其数学模型及汽车悬架系统汽车减震器原理汽车减震器示意图液压减振器数学模型的基本原则不同应用场合下减振器的稳态特性液压减振器的数学模型描述用图2所示的典型减振器特性来说明减振器数学模型中所含参数的物理含义。为了更好理解使用的公式,将减振特性转换为压力差和液压油流量之间的关系。通过将减振力除以活塞面积,将活塞速度乘以活塞面积可以实现这一转换,如图3所示。图2数学模型中参数的物理意义对于适用的减振器类型,D表示减振特性中的泄载点。在这一点阻尼特性将发生改变,从而将第一阻尼率和第二阻尼率区别开

汽车减震器原理并建立其数学模型及汽车悬架系统.ppt
汽车减震器原理并建立其数学模型及汽车悬架系统汽车减震器原理汽车减震器示意图液压减振器数学模型的基本原则不同应用场合下减振器的稳态特性液压减振器的数学模型描述用图2所示的典型减振器特性来说明减振器数学模型中所含参数的物理含义。为了更好理解使用的公式,将减振特性转换为压力差和液压油流量之间的关系。通过将减振力除以活塞面积,将活塞速度乘以活塞面积可以实现这一转换,如图3所示。图2数学模型中参数的物理意义对于适用的减振器类型,D表示减振特性中的泄载点。在这一点阻尼特性将发生改变,从而将第一阻尼率和第二阻尼率区别开

汽车前减震器安装引导装置及汽车前减震器安装方法.pdf
本发明公开了一种汽车前减震器安装引导装置及汽车前减震器的安装方法,能够顺利完成汽车前减震器和车身上的减震器支座的对接安装。其技术方案为:安装引导装置包括导向座、导向杆和导向座固定螺栓,导向座上设有导向座孔,导向杆沿导向座孔自由滑动,导向杆的一端开有盲管状的螺栓导入孔,螺栓导入孔用于插入减震器固定螺栓,导向座固定螺栓用于将安装引导装置临时安装在减震器支座上。

减震器、减震器高度调整方法及汽车.pdf
本发明提供一种减震器、减震器高度调整方法及汽车,其中减震器包括:储油桶、安装座、驱动机构和控制模块;储油桶上固定有齿条,安装座上设置有与齿条相配合的齿轮;驱动机构与齿轮连接,用于驱动齿轮转动,从而带动齿条向上或向下运动;储油桶和安装座之间通过锁孔以及与锁孔相配合的电子锁实现固定;控制模块与电子锁电连接,用于在驱动机构驱动齿轮转动之后,控制电子锁将锁孔锁住。本发明提供的减震器、减震器高度调整方法及汽车,成本低廉,易于工程化,能够方便及时地调整减震器高度,从而可以达到调整整车高度的目的。

汽车减震器检具.pdf
本发明公开了汽车检具领域内的汽车减震器检具,包括底座、支柱、夹钳、定位头。支柱有两个并分别用螺钉固定在底座上端的两侧,每个支柱的顶端均通过螺栓固定有摆块,摆块靠近地板中心的一侧设有摆杆,摆杆的自由端螺纹连接有定位柱。两个支柱中间的底座上通过螺钉固定有两个前、后并列设置的支撑板,支撑板的上端设有V形的定位槽。底座前侧的右端固定有支撑套,所属支撑套内滑动连接有支杆,夹钳铰接在支杆的顶端,夹钳与支杆的铰接处设有棘轮机构,定位头螺纹连接在夹钳上。本方案能有效地对汽车减震器进行定性检测而且结构简单紧凑、制造方便,制
