
数期末复习必备-多元函数积分学——线积分 09624.pdf

qw****27









亲,该文档总共59页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

数期末复习必备-多元函数积分学——线积分 09624.pdf
第十章第十章(1)(1)曲线积分一、主要内容一、主要内容z曲线积分z=f(x,y)1.背景Oy(1)f(x,y)ds(f(x≥,y)0)∫xLL1)以f(x,y)为线密度的曲线构件的质量;2)以L为准线,f(x,y)为高,母线平行于z轴的柱面段的面积:S柱面面积=f(∫x,)yds.L目回上下停r(P2)x∫Qd+yd变力:F=(,)P沿所作的功QL.L2.计算法(1)f∫x(,y,z)的计算sdL方法:1°性质①轴(或面)对称性被积函数有相应2°对称性的利用(的奇偶性)②轮换对称性3°直接法(化为定积分

多元函数积分学复习课.ppt
多元函数积分学复习课例1解例3改换下列二次积分的积分次序.例4改换下列二次积分的积分次序.解例6化为极坐标形式的二次积分.例7设区域计算解1积分区域如图记区域在xOy面的投影区域D的边界曲线为在zOx面的投影区域为思考:例9化为三次积分,其中W由以下曲面所围:提示闭区域可表示为在xOy面的投影区域D在xOy面的投影区域D例13已知曲面S1与曲面S2,它们的方程为例13已知曲面S1与曲面S2,它们的方程为例14已知L为圆周x2+y2=2ax(a>0),计算例14已知L为圆周x2+y2=

多元函数积分学.ppt
CalculusofFunctionsofSeveralVariables二重积分的计算(曲线坐标)三.曲线坐标系下二重积分的计算线的交点标示,也可以用两曲当划分得足够细,因此,在uv曲线坐标系下,解此题积分区域为椭圆,应用广义极坐标例10解在xoy系四条直线的交点为例11解引入曲线坐标换:例12证习题6.2-P.146(A)—N.6,7,9,10,11.

2012考研必备 多元函数积分学4 金典.pdf
2012考研辅导系列内部资料多元函数积分学Youstupidcunt!cunnilinguspenisvagina1§3三重积分的计算三、球坐标系下三重积分的计算空间任意一点M(x,y,z)还可以用球面坐标唯一定位、表示。z球面坐标系如下构成:ρ=ρ∗球心都在原点的同心球面族;∗ϕ=ϕ顶点在原点,对称轴为z轴,半顶角为ϕ的圆锥面族;θ=θ∗从z轴发出的射面族,与xoz坐标面夹角为θ.23z直角坐标到球面坐M=(ρ,ϕ,θ)标的变换公式:zx=ρsinϕcosθϕM(x,y,z)ρyyy=ρsinϕsinθ

2012考研必备 多元函数积分学5 金典.pdf
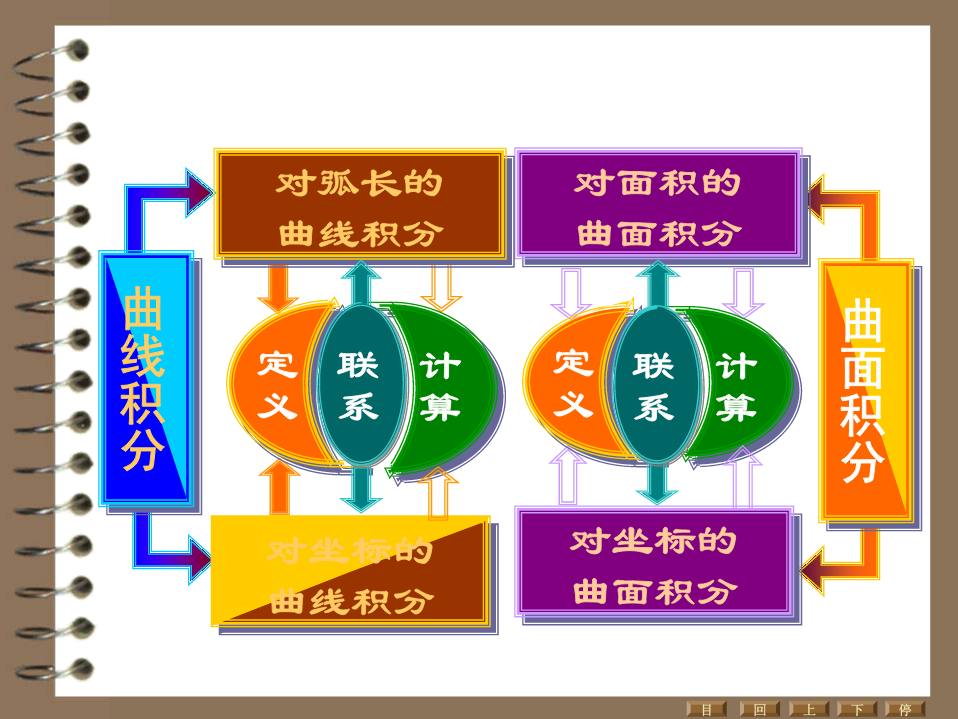
2012考研多元函数积分学-重点与难点辅导系列内部资料返回多元函数积分学-重点与难点返回多元函数积分学-重点与难点返回多元函数积分学-知识网络返回多元函数积分学-知识网络返回多元函数积分学-知识网络返回
