
pn结 半导体物理_第七.ppt

kp****93






亲,该文档总共72页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

pn结 半导体物理_第七.ppt
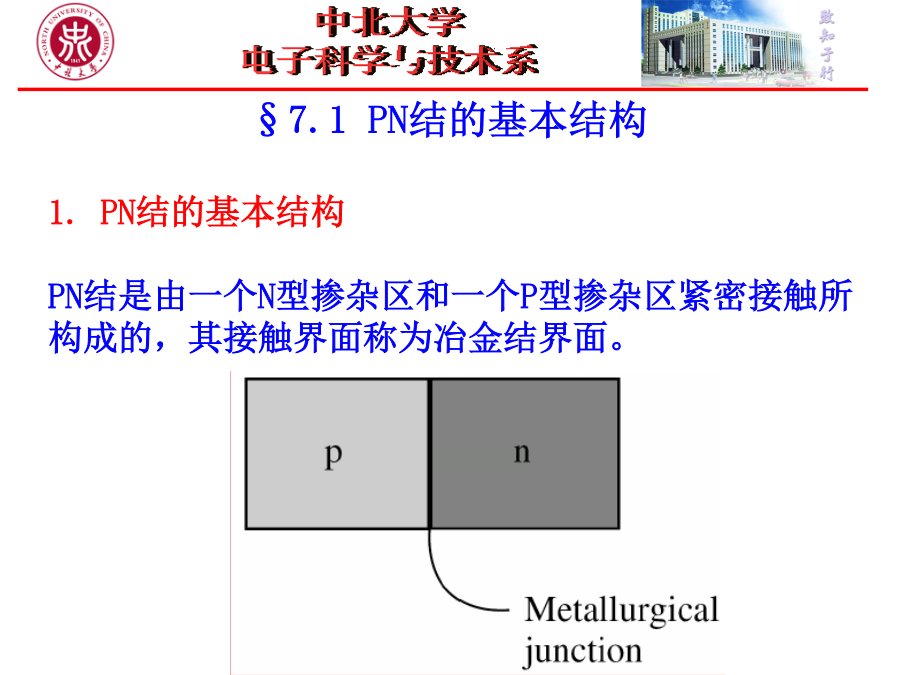
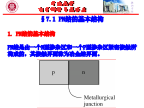
第七章PN结本章学习要点:1.了解PN结的结构及空间电荷区的概念;2.掌握零偏状态下PN结的特性,包括内建电势、内建电场以及空间电荷区宽度等;3.掌握反偏状态下PN结的空间电荷区宽度、内建电场以及PN结电容特性;4.了解非均匀掺杂PN结的特性;§7.1PN结的基本结构1.PN结的基本结构PN结是由一个N型掺杂区和一个P型掺杂区紧密接触所构成的,其接触界面称为冶金结界面。2.制造PN结的方法:(1)外延方法:突变PN结;(2)扩散方法:缓变PN结;(3)离子注入方法:介于突变结与缓变结之间;为简单起见,首先
pn结半导体物理第七.pptx
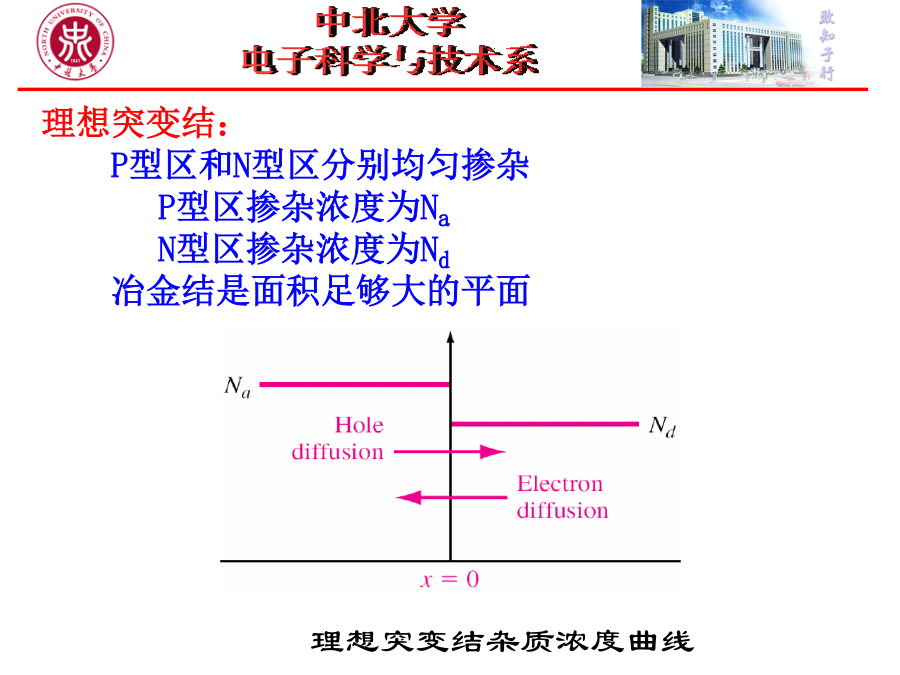
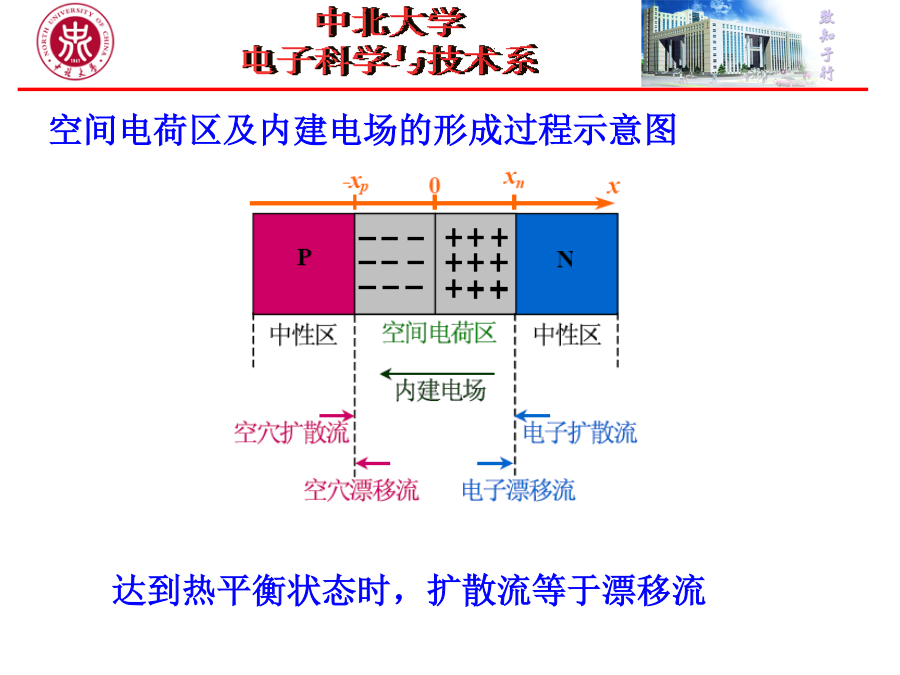
§7.1PN结的基本结构1.PN结的基本结构PN结是由一个N型掺杂区和一个P型掺杂区紧密接触所构成的,其接触界面称为冶金结界面。2.制造PN结的方法:(1)外延方法:突变PN结;(2)扩散方法:缓变PN结;(3)离子注入方法:介于突变结与缓变结之间;为简单起见,首先讨论突变结。理想突变结:P型区和N型区分别均匀掺杂P型区掺杂浓度为NaN型区掺杂浓度为Nd冶金结是面积足够大的平面3.PN结空间电荷区的形成两种材料接触形成PN结时,冶金结两侧将出现载流子密度差,形成可动载流子的扩散流:*电子离开N型区向

半导体物理PN结.pptx
半导体物理第六章PN结什么是PN结?PN结的典型工艺方法(1):杂质浓度从p区到n区逐渐变化,称为缓变结。PN结的形成机理(1):内电场作用促进少子的漂移运动,使N区的少子空穴向P区漂移,P区的少子电子向N区漂移,漂移运动的方向正好与扩散运动的方向相反。从N区漂移到P区的空穴补充了原来交界面上P区所失去的空穴,从P区漂移到N区的电子补充了原来交界面上N区所失去的电子,这就使空间电荷减少,内电场减弱。因此,漂移运动的结果是使空间电荷区变窄,扩散运动加强。最后,多子的扩散和少子的漂移达到动态平衡。在P型半导体

半导体物理基础PN结PPT.ppt
半导体物理基础PN结PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结根据公式(2-6-3)反向电流随温度升高而增加。单边突变结的耗尽层宽度为(耗尽近似)9电荷存储和反向瞬变层宽度W

半导体物理基础----PN结PPT.ppt
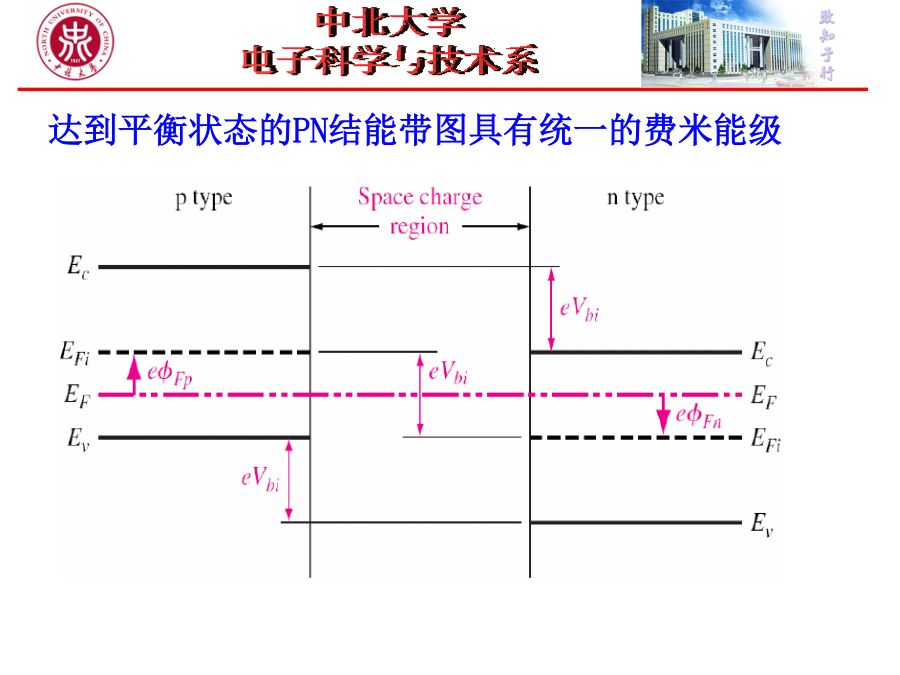
半导体物理基础PN结PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程PN结制作工艺过程2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结2.1热平衡PN结在空间电荷区,载流子浓度不发生变化,因此准费米能级不变。2-3理想PN结的直流电流-电压特性该电场将使得电子有类似的分布,以中和过
