导数与单调性.ppt

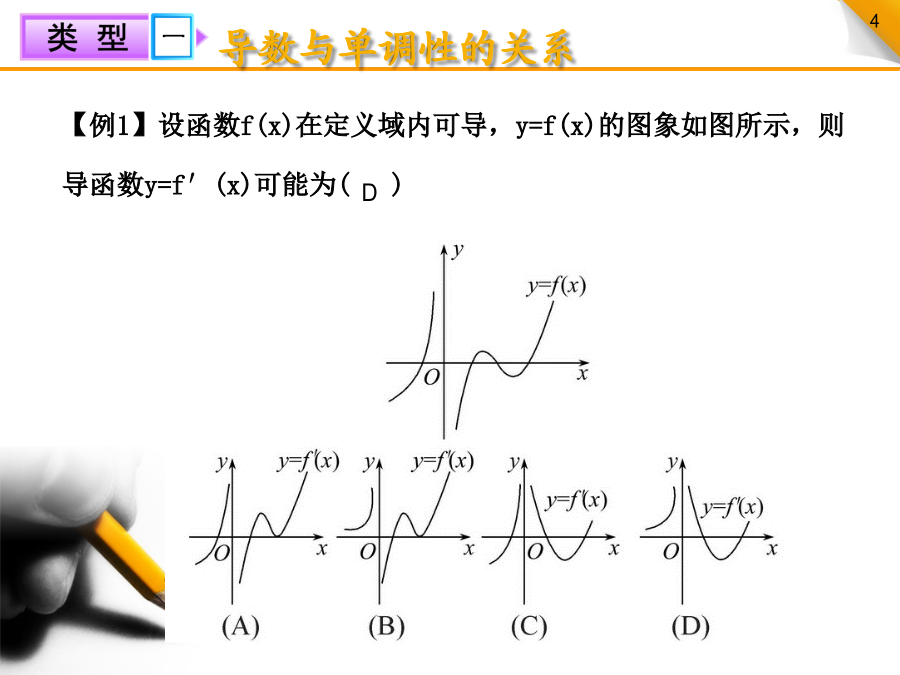
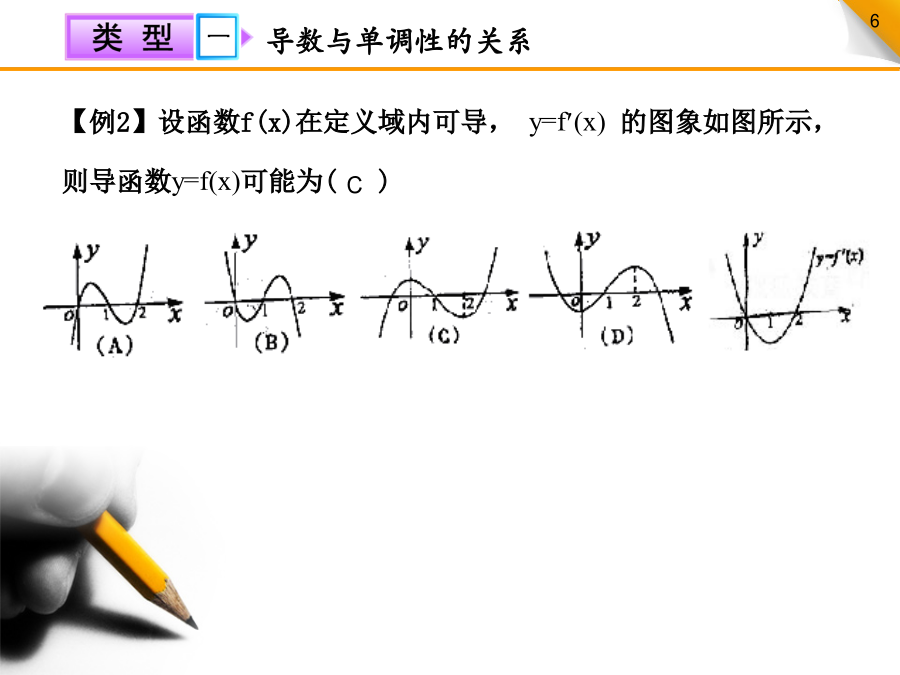
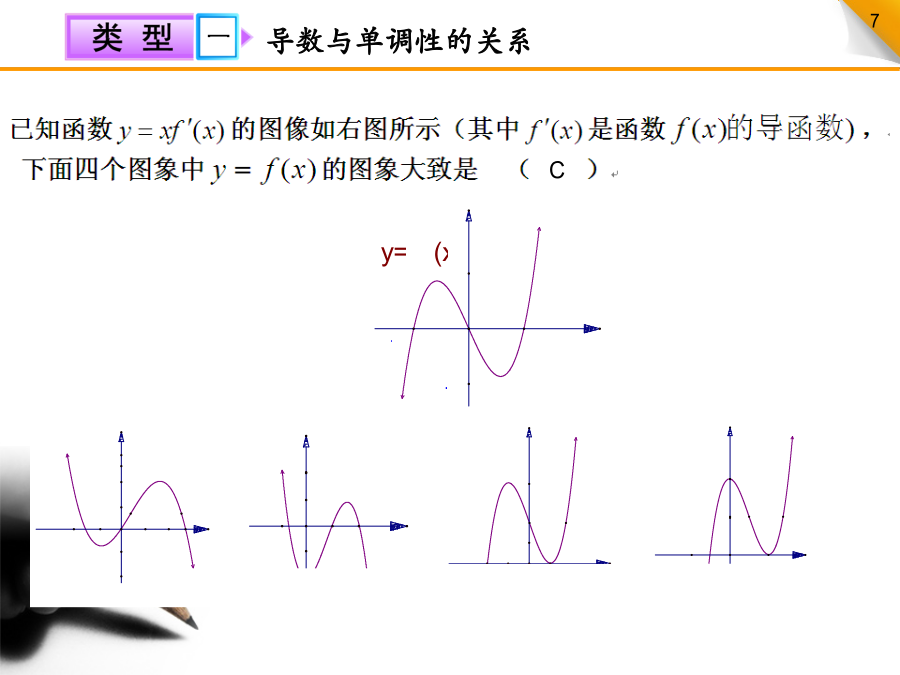
函数的单调性与导数1.利用导数符号判断单调性的方法：利用导数判断函数的单调性比利用函数单调性的定义简单的多，只需判断导数在该区间内的正负即可.2.通过图象研究函数单调性的方法.(1)观察原函数的图象重在找出“上升”“下降”产生变化的点，分析函数值的变化趋势；(2)观察导函数的图象重在找出导函数图象与x轴的交点，分析导数的正负.函数的正负与导数的正负没有关系.导数与单调性的关系【审题指导】由函数y=f(x)的图象可得到函数的单调情况，进而确定导数的正负，再“按图索骥”.【规范解答】选D.由函数的图象知：当x＜0时，函数单调递增，导数始终为正；当x＞0时，函数先增后减再增，导数先正后负再正，对照选项，应选D.【例2】设函数f(x)在定义域内可导，y=f′(x)的图象如图所示，则导函数y=f(x)可能为()导数与单调性的关系1.利用导数求函数的单调区间：(1)求定义域;(2)解不等式f′(x)＞0(或f′(x)＜0);(3)把不等式的解集与定义域求交集得单调区间.(1)单调区间不能“并”，即不能用“∪”符号连接，只能用“，”或“和”隔开.(2)导数法求得的单调区间一般用开区间表示.【例1】已知求f(x)的单调区间.【审题指导】要求f(x)的单调区间，可确定定义域后，再讨论使f′(x)>0和f′(x)<0的x的范围，即得f(x)的单调区间，利用导数求函数的单调区间利用导数求函数的单调区间由单调性求参数范围时的注意事项：若函数f(x)可导，其导数与函数的单调性的关系如下：以增函数为例来说明：①f′(x)＞0能推出f(x)为增函数，但反之不一定.即f′(x)＞0是f(x)为增函数的充分不必要条件.②f′(x)≠0时，f′(x)＞0是f(x)为增函数的充分必要条件.③f(x)为增函数，一定可以推出f′(x)≥0，但反之不一定，即f′(x)≥0是f(x)为增函数的必要不充分条件.已知单调性求参数时，特别注意“=”的处理.【例3】已知函数f(x)=ax3+3x2-x+1在R上是减函数，求a的取值范围.【审题指导】f(x)是减函数，则必有f′(x)≤0，可从f′(x)≤0入手，再检验使f′(x)=0时参数a的值是否符合题意.【规范解答】函数的导数f′(x)=3ax2+6x-1.由f′(x)=3ax2+6x-1≤0(x∈R)得∴a≤-3；当a=-3时，f′(x)=-9x2+6x-1=-(3x-1)2，只在时，f′(x)=0，f(x)仍是R上的减函数.∴所求a的取值范围是(-∞,-3］.【互动探究】把本例中“在R上是减函数”改为“在R上是单调函数”，求实数a的取值范围.【解题提示】分f(x)是单调增函数和单调减函数两种情况讨论.【解析】∵f′(x)=3ax2+6x-1,∴当f(x)是单调增函数时，由f′(x)≥0得∴a∈，当f(x)是单调减函数时，由例3得a∈(-∞,-3］，∴函数f(x)=ax3+3x2-x+1在R上是单调函数，则实数a的取值范围是(-∞,-3］.【变式训练】设a为实数，函数f(x)=x3-ax2+(a2-1)x在(-∞,0)上是增函数，求a的取值范围.(2)若Δ=12－8a2>0,即即时在区间(-∞,0)上恒有f′(x)＞0,即在(-∞,0)上是增函数,综上所述函数的极值与导数