
《导数的单调性与导数》课件.pptx

仙人****88









亲,该文档总共18页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

《导数的单调性与导数》课件.pptx
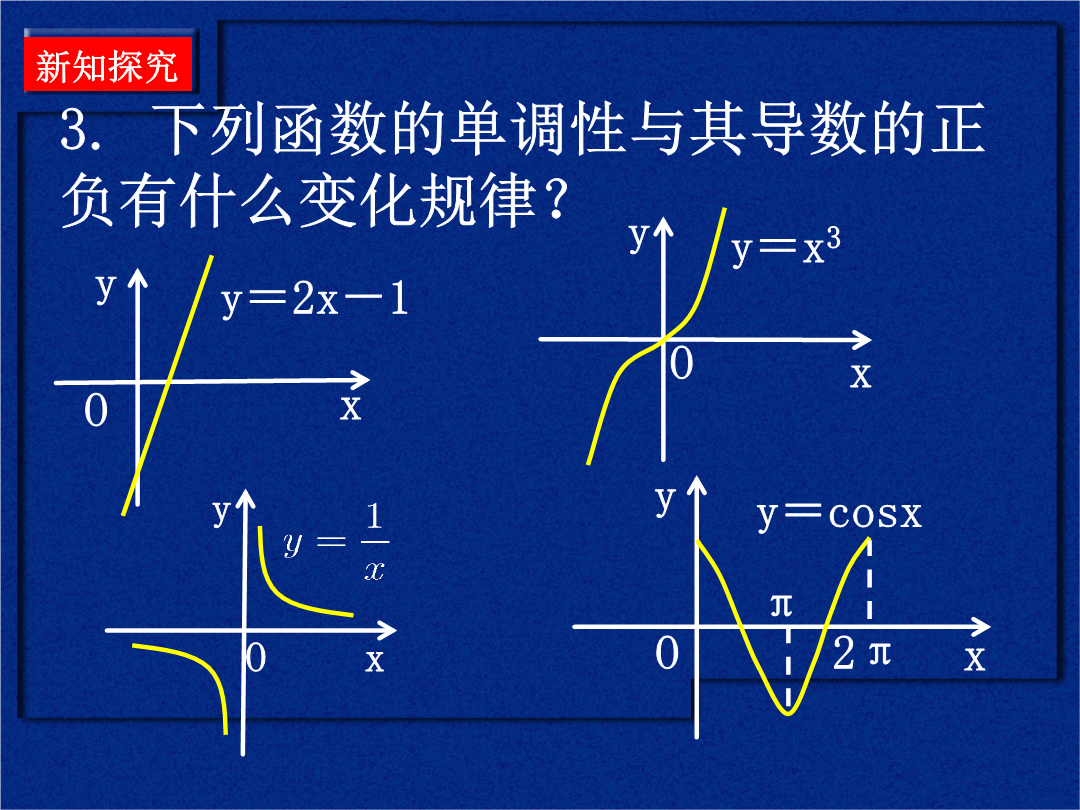
1.3导数在研究函数中的应用知识回顾新知探究2.函数f(x)=x2-4x+3的单调性与其导数有什么内在联系?3.下列函数的单调性与其导数的正负有什么变化规律?一般地,函数f(x)在区间(a,b)内的单调性与其导数的关系是1.若函数f(x)在区间(a,b)内恒有f′(x)=0,则函数f(x)有什么特性?2.若函数f(x)在区间(a,b)内有f′(x)≥0(或f′(x)≤0),且不恒等于0,则f(x)的单调性如何?3.函数f(x)=x2在区间(0,1)和(1,2)内递增的快慢程度如何?函数f(x)=在区间(0

函数的单调性与导数课件.ppt
函数y=f(x)在给定区间G上,当x1、x2∈G且x1<x2时以前,我们主要采用定义法去判断函数的单调性.在函数y=f(x)比较复杂的情况下,比较f(x1)与f(x2)的大小并不容易.如果利用导数来判断函数的单调性就比较简单.x例1已知导函数的下列信息:例2判断下列函数的单调性,并求出单调区间:(2)因为,所以解:(4)因为,所以求可导函数f(x)单调区间的步骤:(1)求f’(x)(2)解不等式f’(x)>0(或f’(x)<0)(3)确认并指出递增区间(或递减区间)练习P2611.判断下列函数的单调性,并

函数的单调性与导数ppt课件.ppt
1.3.1函数的单调性与导数温故知新问题1:导数的几何意义?x1思考:那么判断下列函数的单调性?高台跳水运动员的高度h随时间t变化的函数h(t)=-4.9t2+6.5t+10再观察下面一些函数的图象,探讨导函数的正负与其对应函数的单调性的关系:导数f(x0)表示函数f(x)在点(x0,f(x0))处的切线的斜率例1.已知导函数f(x)的下列信息:解:(3)f(x)=____________例2.判断下列函数的单调性,并求出单调区间:④解不等式f(x)<0,解集在定义域内的部分为减区间;练习例3.如

331函数的单调性与导数(课件).ppt
西藏日喀则地区上海实验学校第三章导数及其应用说课稿(一)复习巩固:o定理:一般地,函数第一步:确定函数例题:课堂练习:(四)小结:求函数谢谢!再见!

《函数的单调性与导数》课件1.ppt
3.3导数在研究函数中的应用1.知识与技能结合实例,借助几何直观发现函数的单调性与导数的关系.2.过程与方法能利用导数研究函数的单调性,会求不超过三次的多项式函数的单调区间.本节重点:利用求导的方法判断函数的单调性.本节难点:函数的导数与单调性的关系.1.用导数去研究函数的单调性比用定义法更为简便,是导数几何意义在研究曲线变化规律时的一个重要应用,它充分体现了数形结合的基本思想.因此,必须重视对数学思想、方法进行归纳总结,提高应用数学思想、方法解决问题的熟练程度,达到优化解题思路、简化解题过程的目的.2.
