
《信号与线性系统》期末试卷.pdf

文库****品店





在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

《信号与线性系统》期末试卷.pdf
《信号与线性系统》期末试卷2012-2013学年第⼆学期《信号与线性系统》(课内)试卷A卷⼀、计算题(共45分)1.(5分)计算积分dtttt)6()sinπ(δ-+?+∞∞-的值。2.(5分)绘出函数)1()]1()([-+--tut的波形图。utut3.(6分)已知)2()()(),1()()(21--=--=tutut,求卷积ftutu)()(21ttff。tf*4.(6分)若)(t的傅⾥叶变换已知,记为f)(ωF,求)1()1(tf对应的傅⾥叶变换。t--5.(6分)如下图所⽰信号,已知其傅⾥叶变
信号与线性系统.ppt
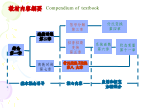
教材内容纲要第二章连续时间系统的时域分析§2.1引言系统分析的基本任务是在给定系统和输入的条件下,求解系统的输出响应。所谓系统的模型是指对系统物理特性的抽象,用数学表达式或具有理想特性的符号图形来表征系统特性。数学模型---以数学表达式表征系统特性。举例2:双耦合电路对图示电路列写电流和电压的微分方程。电阻R的伏安关系:整理后得:举例3.对图示电路,写出激励e(t)和响应r(t)间的微分方程。*由以上例题可以得出如下结论:1.求得的微分方程阶数与电路的阶数一致。例2:含有4个储能元件,故为四阶电路。例3:

信号与线性系统分析试题——2005期末试卷.pdf

总复习(信号与线性系统).ppt
信号与线性系统内容回顾内容回顾1连续信号的时域描述及运算注意积分区间1.2信号的运算注意:例:已知f(1-2t)如图所示,求f(t)的波形。1)齐次性例2:已知某线性时不变系统:当激励e(t)=ε(t),初始状态x1(0-)=1,x2(0-)=2时,响应2、连续时间系统的时域分析2.1求解系统零输入响应的一般步骤:例1:已知某系统激励为零,初始值r(0)=2,r’(0)=1,r”(0)=0,描述系统的传输算子为a)求传输算子H(p);b)如果m≥n,用长除法将H(p)化为真分式;c)H(p)部分分式;d)

《信号与线性系统》试题与答案.pdf
..如图离散因果系统框图,为使系统稳定,求常量a的取值范围2∑z1∑F(z)Y(z)a解:设加法器输出信号X(z)X(z)=F(z)+a/Z*X(z)Y(z)=(2+1/z)X(z)=(2+1/z)/(1-a/z)F(z)H(z)=(2+1/z)/(1-a/z)=(2z+1)/(z-a)为使系统稳定,H(z)的极点必须在单位园内,故|a|<1121周期信号f(t)=1costsint243436试求该周期信号的基波周期T,基波角频率Ω,画出它的单边频谱图,并求f(
