随机过程-2-平稳过程.pptx

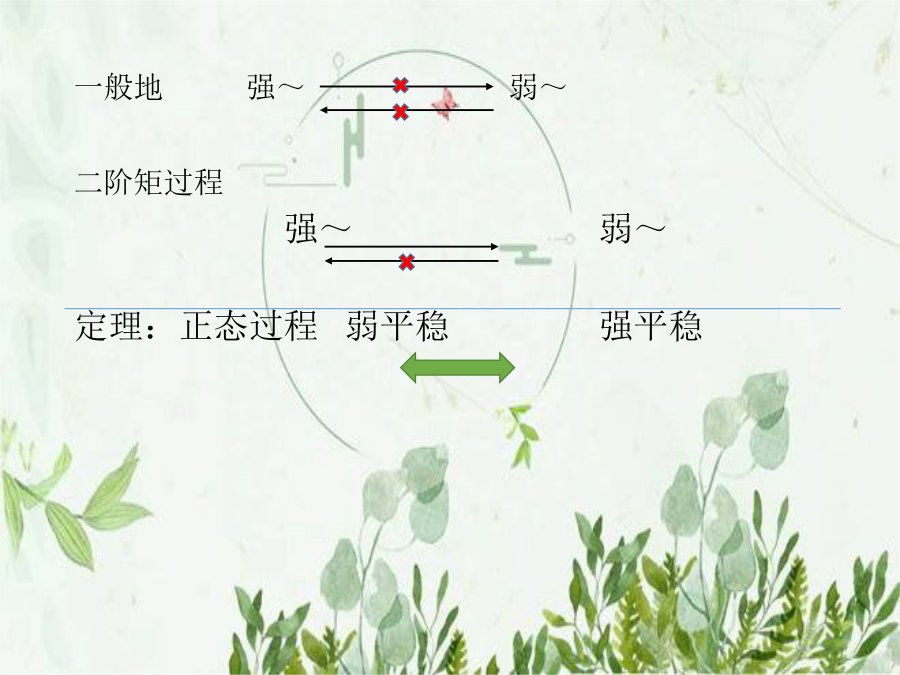
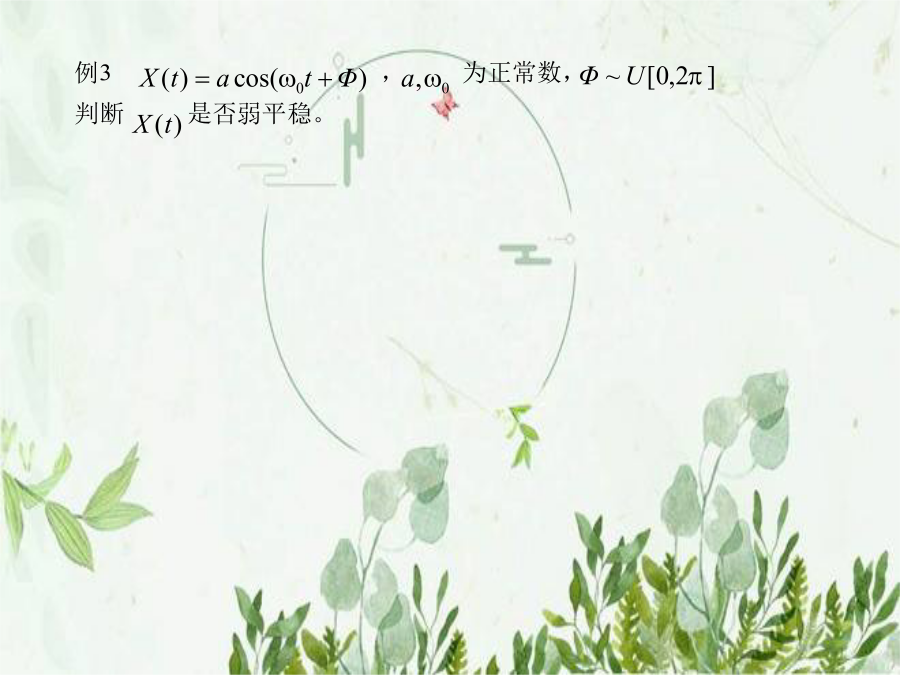
随机过程-2-平稳过程.pptx§1平稳过程概念连续一维二维与t无关，一元函数定义：设的一、二阶矩存在，若与t无关，则称之为弱（宽、广义）平稳（随机）过程。一般地强～弱～二阶矩过程强～弱～定理：正态过程弱平稳强平稳下面均讨论弱平稳随机过程例1随机序列，X(n)两两不相关，例2随机序列，X(n)两两不相关，N为自然数，为常数。称为离散白噪声的滑动和。推广：且收敛。称为离散白噪声的无限滑动和。例3，为正常数，判断是否弱平稳。例4，为正常数，A,B独立，判断是否弱平稳。例5，X(t)只取，内正负号变化次数记为，服从参数为的泊松分布。判断X(t)的平稳性。复平稳过程定义：是复随机过程，若且仅与有关，而与无关，即则称是复平稳随机过程。例6，其中是实数，是不相关的复随机变量，讨论的平稳性。，是不相关的复随机变量，讨论的平稳性。复平稳过程的协方差函数§2相关函数的性质（3）（4）非负定，即也具有同样的四条性质。连续平稳过程的相关函数定理：是平稳过程，它在T上连续的充要条件是在处连续，亦可得此时在T上连续。定理：是宽平稳过程，则以下各项等价均方连续在点均方连续在上连续在处连续二、互相关函数及其性质定义：两个平稳过程，若互相关函数不依赖于t，则称X(t)与Y(t)是平稳相关的。此时，平稳相关随机过程互相关函数的性质（也具有相同的性质）§3各态历经性定义：为平稳过程，若存在，则称之为平稳随机过程X(t)在区间上的时间平均。若存在，则称之为平稳随机过程X(t)在区间上的时间相关函数。为X(t)的各态历经性。例1，为正常数，讨论的各态历经性。例2，X为具有一、二阶矩的随机变量，但不服从单点或两点分布讨论X(t)的各态历经性。二、各态历经定理定理1为平稳过程，则的充要条件是推论：若平稳随机过程X(t)满足条件即则例3，有，，讨论X(t)是否具有数学期望的各态历经性。定理2：若，有为平稳过程，则成立的充要条件是其中定理3：为平稳过程，则的充要条件是定理4：为平稳过程，则的充要条件是定理5：为平稳序列，则的充要条件是定理6：为平稳序列，，则的充要条件是其中三、各态历经定理的应用定义：以及X,若，有或则称依概率收敛到X，记为定理7：若，则即均方收敛强于依概率收敛。要求T，N很大，且T/N很小T，N-r很大，T/N很小，