
高考数学第1轮总复习 全国统编教材 12.4导数的概念与运算课件 理 课件.ppt

冷霜****魔王




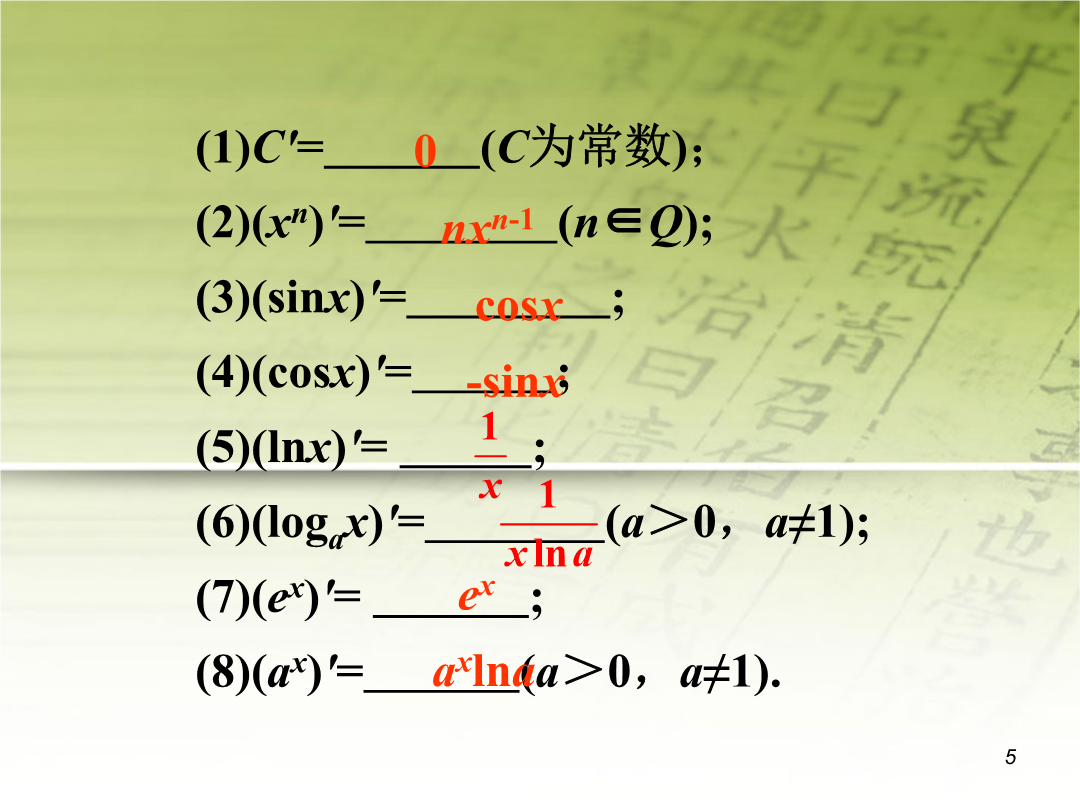





亲,该文档总共35页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

高考数学第1轮总复习 全国统编教材 12.4导数的概念与运算课件 理 课件.ppt
第十二章极限与导数考点搜索1.对于函数y=f(x)记Δy=f(x0+Δx)-f(x0)如果当Δx→0时有极限就说函数y=f(x)在x0处可导并把这个极限叫做f(x)在点x0处的导数(或变化率)记作f′(x0)或y′|x=x0即f′(x0)=———————=——————————————.2.如果函数f(x)在开区间(ab)内每一点都可导则对(ab)内每一个确定的值x0都对应着一个确定的导数f′(x0)这样就在开区间(ab)内构成一个新的函数称这一新函

高考数学第1轮总复习 全国统编教材 3.1数列的概念课件 理 课件.ppt
第三章数列考点搜索一、数列的定义1.按①排成的一列数叫做数列其一般形式为a1a2…an…简记为{an}.2.数列是一种特殊的函数其特殊性表现在它的定义域是正整数集或正整数集的子集因此它的图象是②.二、数列的通项公式一个数列{an}的第n项an与项数n之间的函数关系如果可以用一个公式an=f(n)来表示我们就把这个公式叫做这个数列的通项公式.三、数列的分类1.按照项数是有限还是无限来分:有穷数列、无穷数列.

高考数学第1轮总复习 全国统编教材 9.5空间向量及其运算课件 理 课件.ppt
第九章直线、平面、简单几何体考点搜索1.空间向量:在空间我们把具有_____和_____的量叫做向量空间向量也用__________表示并且____________________的有向线段表示同一向量或相等的向量.2.空间向量的加法减法与数乘向量:如下图我们定义空间向量的加法减法与数乘向量为:=_______=________=____(λ∈R).3.空间向量的加法与数乘向量运算满足如下运算律:(1)加法交换律:_______________;

高考数学第1轮总复习 全国统编教材 12.5导数的应用(第3课时)课件 理 课件.ppt
第十二章极限与导数题型6利用导数证明不等式所以当x∈(0+∞)时恒有f(x)>f(0)=0即x3>x2-ln(x+1)恒成立.故当x∈(0+∞)时有ln(x+1)>x2-x3.对任意正整数n取∈(0+∞)则有所以结论成立.点评:利用导数证明不等式一般是先根据不等式的形式构造相对应的函数然后利用导数讨论此函数的单调性或最值进一步得到所需结论.已知mn是正整数且2≤m<n.证明:(1+m)n>(1+n)m.证明:不等式

高考数学第1轮总复习 全国统编教材 5.1向量的概念及其几何运算(第2课时)课件 理 课件.ppt
第五章平面向量题型3共线向量与三点共线问题解:因为所以所以向量与共线故M、N、C三点共线.点评:用向量法证明几何中的平行或共线问题就是用向量表示图中的有关线段利用向量的相等得到线线平行或多点共线如本题中的三点共线即从这三点中任取两点构成向量然后看这两个向量是否是共线向量.设E、F分别是四边形ABCD的对角线AC、BD的中点试推断向量与
