4 直线与圆、圆与圆的位置关系课件 (理) 新人教A版 课件.ppt

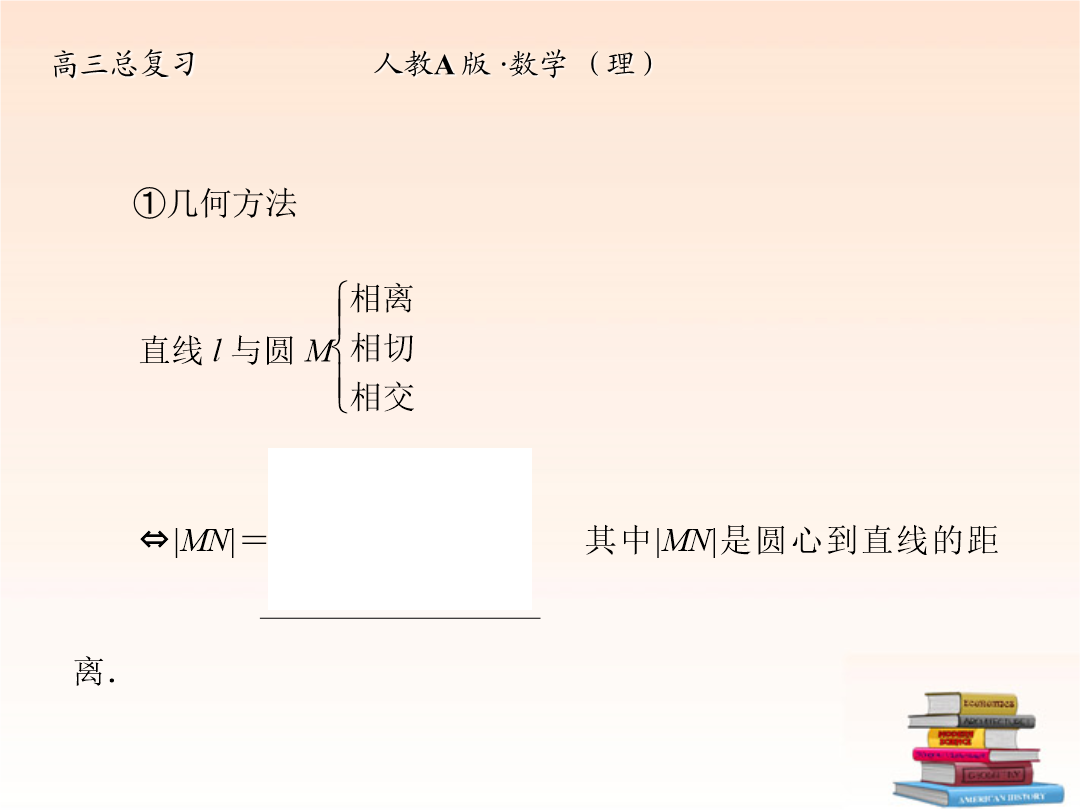
1.能根据给定直线、圆的方程判断直线与圆的位置关系；能根据给定两个圆的方程判断两圆的位置关系；2．能用直线和圆的方程解决一些简单的问题；3．初步了解用代数方法处理几何问题的思想．1．直线与圆的位置关系(1)直线与圆的位置关系有三种：(2)直线l：Ax＋By＋C＝0与圆(x－a)2＋(y－b)2＝r2(r>0)的位置关系的判定方法有两种：①几何方法(3)计算直线被圆截得的弦长的常用方法：①几何方法运用弦心距(即圆心到直线的距离)、半弦长及半径构成直角三角形计算．②代数方法运用韦达定理及弦长公式|AB|＝.2．圆与圆的位置关系的判定设⊙C1：(x－a1)2＋(y－b1)2＝r(r1>0)⊙C2：(x－a2)2＋(y－b2)2＝r(r2>0)则有⇔⊙C1与⊙C2相离；⇔⊙C1与⊙C2相切；⇔⊙C1与⊙C2相交；⇔⊙C1与⊙C2内切；⇔⊙C1与⊙C2内含．5．已知两圆x2＋y2＝10和(x－1)2＋(y－3)2＝20相交于AB两点则直线AB的方程是________．解析：两圆方程分别为x2＋y2－10＝0x2＋y2－2x－6y－10＝0两方程相减得直线AB方程为2x＋6y＝0即x＋3y＝0.答案：x＋3y＝0热点之一直线与圆的位置关系直线与圆的位置关系有相离(没有公共点)、相切(只有一个公共点)、相交(有两个公共点)三种判断直线与圆的位置关系主要有两种方法：一是圆心到直线的距离与圆的半径比较大小；二是直线与圆的方程组成的方程组解的个数．[例1]当a为何值时直线x＋y－2a＋1＝0与圆x2＋y2－2ax＋2y＋a2－a＋1＝0相切？相离？相交？[思路探究]通过圆心到直线的距离与圆的半径比较大小判断直线与圆的位置关系．[课堂记录]圆的方程可化为(x－a)2＋(y＋1)2＝a可知a>0.圆心(a－1)到直线x＋y－2a＋1＝0的距离热点之二圆的切线、弦长问题1．(1)求圆的切线方程一般有两种方法：①代数法：设切线方程为y－y0＝k(x－x0)与圆的方程组成方程组消元后得到一个一元二次方程然后令判别式Δ＝0进而求得k.②几何法：设切线方程为y－y0＝k(x－x0)利用点到直线的距离公式表示出圆心到切线的距离d然后令d＝r进而求出k.两种方法一般来说几何法较为简洁可作为首选．(2)若点M(x0y0)在圆x2＋y2＝r2上则过M点的圆的切线方程为x0x＋y0y＝r2.[思维拓展]本题第(1)、(2)问是已知一点求直线方程可用点斜式其等量关系是圆心到直线的距离；第(3)问可用坐标转移法求轨迹方程．热点之三圆与圆的位置关系1．判断两圆的位置关系常用几何法即用两圆圆心距离与两圆半径和与差之间的关系一般不采用代数法．2．若两圆相交则两圆公共弦所在直线的方程可由两圆的方程作差消去x2y2项即可得到．[思路探究]根据两圆的位置关系及圆的性质建立等式求出圆O2的半径r2即可．直线与圆的位置关系为历年考试命题的重点多为选择、填空题．但也有许多以此知识为载体的创新问题如2009江苏高考考查了弦长问题属中档题．(2)设P为平面上的点满足：存在过点P的无穷多对互相垂直的直线l1和l2它们分别与圆C1和C2相交且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等．试求所有满足条件的点P的坐标．因为圆C1和C2的半径相等及直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等所以圆C1的圆心到直线l1的距离和圆C2的圆心到直线l2的距离相等即整理得|1＋3k＋ak－b|＝|5k＋4－a－bk|从而1＋3k＋ak－b＝5k＋4－a－bk或1＋3k＋ak－b＝－5k－4＋a＋bk即(a＋b－2)k＝b－a＋3或(a－b＋8)k＝a＋b－5