（课标专用 5年高考3年模拟A版）高考数学 第五章 平面向量 2 平面向量的数量积及平面向量的应用课件 文-人教版高三全册数学课件.pptx

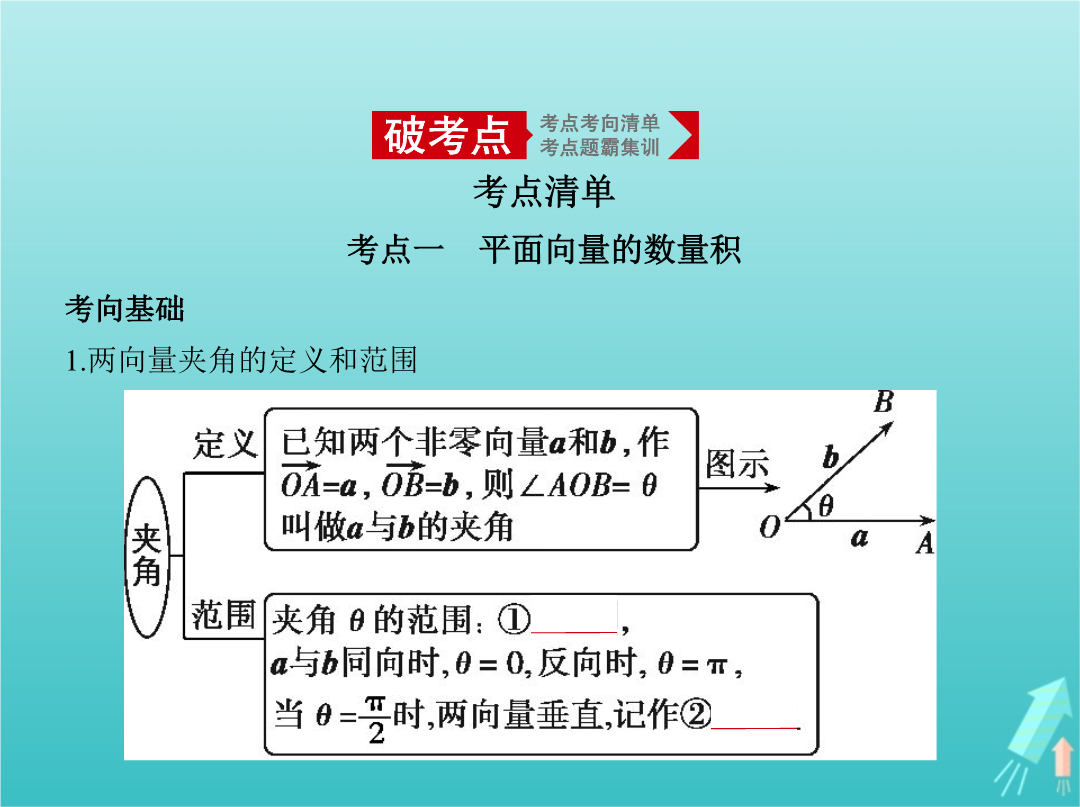
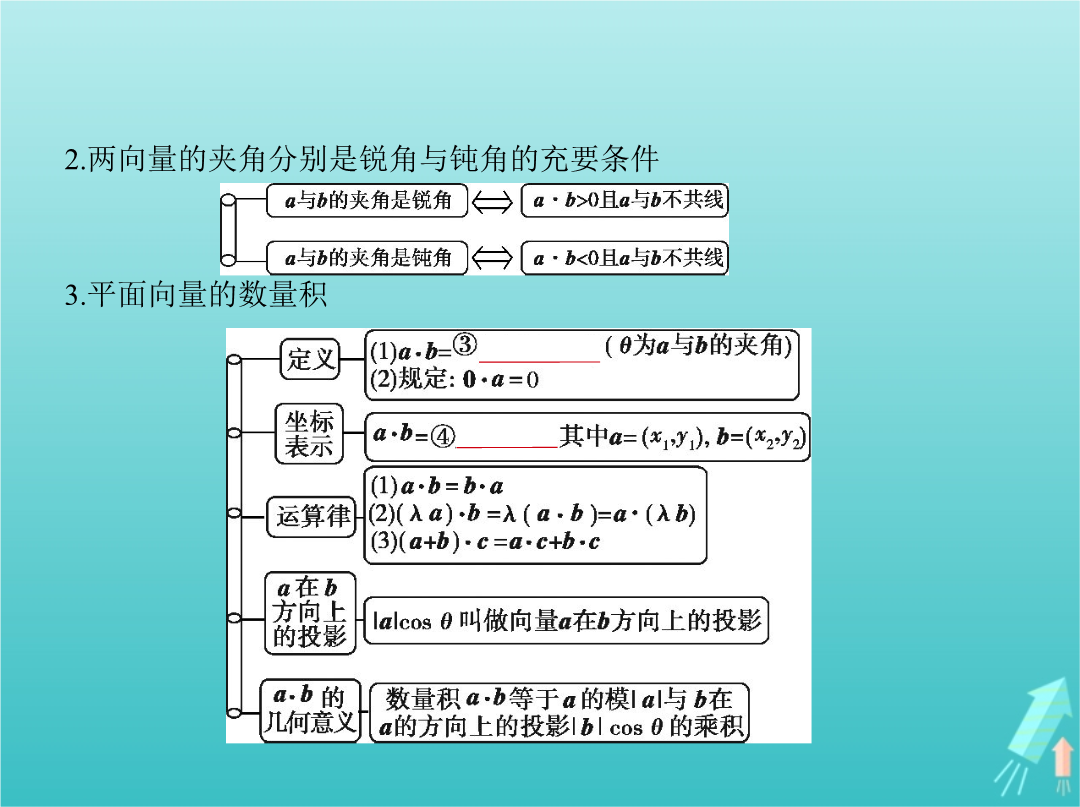
§5.2平面向量的数量积及平面向量的应用考点清单考点一平面向量的数量积考向基础1.两向量夹角的定义和范围 2.两向量的夹角分别是锐角与钝角的充要条件3.平面向量的数量积 4.向量数量积的性质设ab都是非零向量e是与b方向相同的单位向量θ是a与e的夹角则(1)e·a=a·e=⑤|a|·cosθ.(2)当a与b同向时⑥a·b=|a||b|;当a与b反向时⑦a·b=-|a||b|.特别地a·a=⑧|a|2.(3)|a·b|≤|a|·|b|.5.坐标表示若a=(xy)则a·a=a2=|a|2=x2+y2|a|=⑨ .考向突破考向求平面向量的数量积考点二平面向量数量积的应用考向基础1.向量数量积的应用已知a=(x1y1)b=(x2y2).(1)证明垂直问题常用向量垂直的充要条件a⊥b⇔a·b=0⇔x1x2+y1y2=0.(2)求解夹角问题常利用夹角公式:cosθ= = (其中θ为a与b的夹角).(3)求线段长度问题常利用向量的模长公式:|a|= = 或| |= .2.向量中常用的结论在△ABC中∠A∠B∠C所对的边分别为abc.(1)在 =λ 的条件下存在λ使得I为△ABC的内心;a +b +c =0⇔P为△ABC的内心.(2)| |=| |=| |⇔P为△ABC的外心.(3) + + =0⇔G为△ABC的重心.(4) · = · = · ⇔P为△ABC的垂心.考向突破考向一求平面向量的夹角考向二求平面向量的模方法技巧方法1平面向量模长的求解方法利用向量数量积求解长度问题是向量数量积的重要应用要掌握此类问题的处理方法:1.a2=a·a=|a|2或|a|= .2.|a±b|= = .3.若a=(xy)则|a|= 或|a|2=x2+y2.例1(2018河南安阳调研15)已知直角梯形ABCD中AD∥BC∠ADC=90°AD=2BC=1P是腰DC上的动点则| +3 |的最小值为.解析建立平面直角坐标系如图所示则A(20)设P(0y)C(0b)则B(1b).所以 +3 =(2-y)+3(1b-y)=(53b-4y)所以| +3 |= (0≤y≤b)所以当y= b时| +3 |取得最小值5. 方法2平面向量夹角的求解方法1.定义法:利用向量数量积的定义知cosθ= 其中两个向量的夹角θ∈[0π]求解时应求出三个量:a·b|a||b|或找出这三个量之间的关系.2.坐标法:若a=(x1y1)b=(x2y2)θ为ab的夹角则cosθ= .3.三角函数法:可以把所求两向量的夹角放到三角形中利用正、余弦定理和三角形的面积公式等内容进行求解.解题导引一题多解如图设 =a =b则 =a-b以ab为邻边作平行四边形OADB则由题可知四边形OADB为菱形且∠AOB=60°故a与a+b的夹角为∠AOD=30°. 方法3用向量法解决平面几何问题1.用向量法解决平面几何问题的基本步骤:①建立平面几何与向量的联系用向量表示问题中涉及的几何元素将平面几何问题转化为向量的问题;②通过向量运算研究几何元素之间的关系如距离、夹角等问题;③把运算结果转化成几何关系.2.用向量法解平面几何问题主要是通过建立平面直角坐标系将问题坐标化然后利用平面向量的坐标运算求解有关问题这样可以避免繁杂的逻辑推理同时加强了数形结合思想在解题中的应用.解题导引解析解法一:由题意可知 = +  =-  + .因为 · =1所以( + )· =1即 +  · -  =1. ①因为| |=1∠BAD=60°所以 · = | |因此①式可化为1+ | |- | |2=1.解得| |=0(舍去)或| |= 所以AB的长为 .解法二:以A为原点AB所在直线为x轴建立如图所示的直角坐标系过D作DM⊥AB于点M.由AD=1∠BAD=60°可知AM= DM= ∴D .设| |=m(m>0)则B(m0)C 因为E是CD的中点所以E .所以 =  = . 由 · =1可得  + =1即2m2-m=0所以m=0(舍去)或m= .故AB的长为 .