（课标专用 5年高考3年模拟A版）2021高考数学 专题五 平面向量 2 平面向量的数量积及平面向量的应用课件 文.pptx

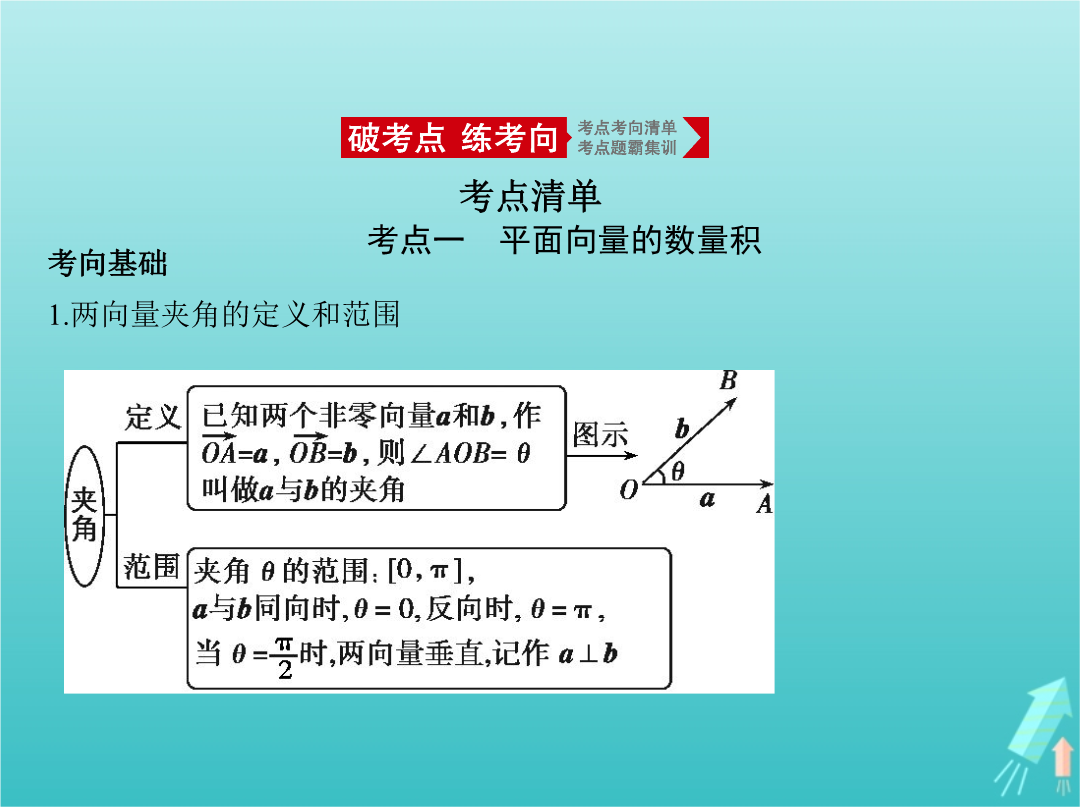
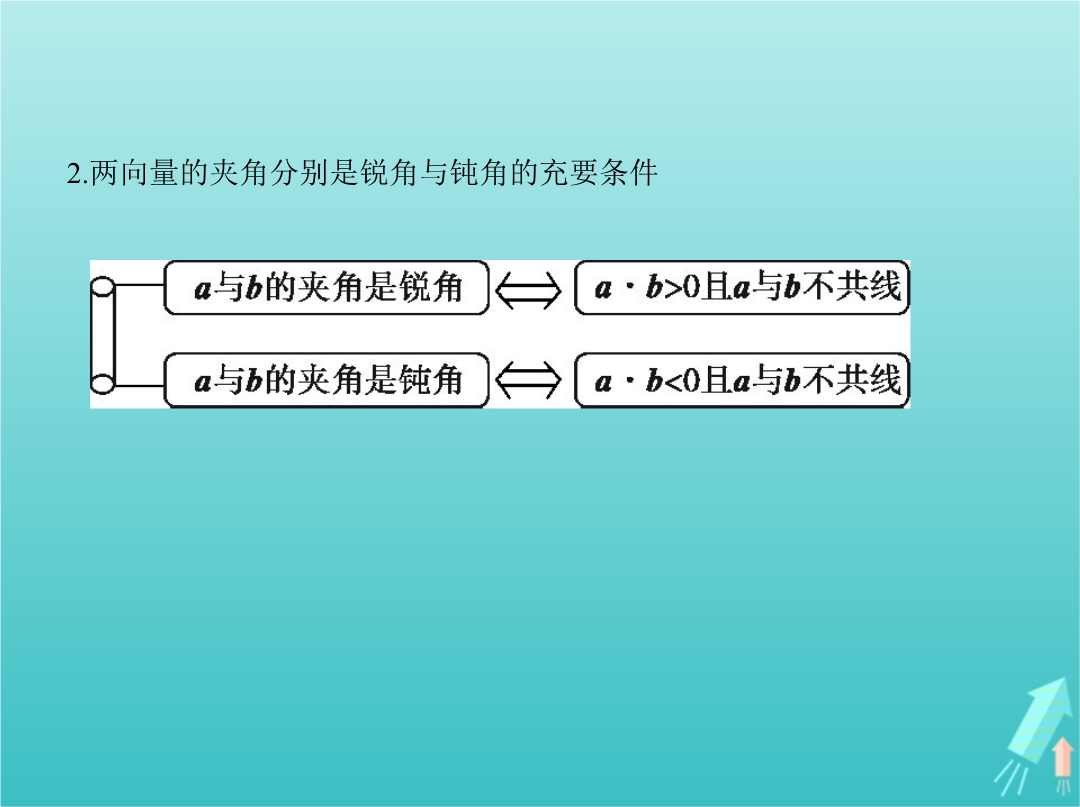
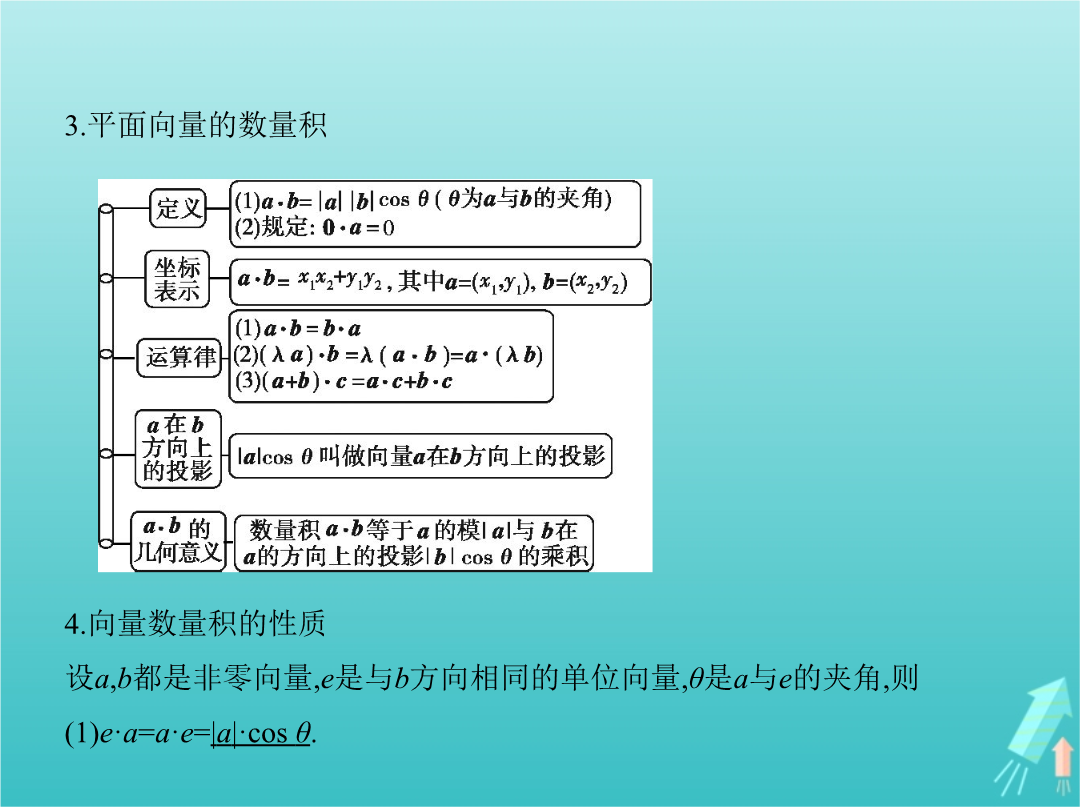
专题五平面向量§5.2平面向量的数量积及平面向量的应用考点一平面向量的数量积2.两向量的夹角分别是锐角与钝角的充要条件3.平面向量的数量积 4.向量数量积的性质设a,b都是非零向量,e是与b方向相同的单位向量,θ是a与e的夹角,则(1)e·a=a·e=|a|·cosθ.(2)当a与b同向时,a·b=|a||b|;当a与b反向时,a·b=-|a||b|.特别地,a·a=|a|2.(3)|a·b|≤|a|·|b|.5.坐标表示若a=(x,y),则a·a=a2=|a|2=x2+y2,|a|= .考向一求平面向量的数量积解析(1) = - =(m+3,3),∵| |=3,∴(m+3)2+9=9,∴m=-3,∴ =(-3,1),∵ =(3,2),∴ · =-9+2=-7.(2)试题考查平面向量的概念、运算、平面向量数量积等数学知识.试题解法灵活多样,考查化归与转化的数学思想,体现了理性思维的学科素养.考查了逻辑推理能力、运算求解能力,落实了基础性的考查要求.a·b+b·c+c·a=b·(a+c)+c·a=-(a+c)2+c·a=-a2-c·a-c2=-4.考向二求平面向量的投影考点二平面向量数量积的应用在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c.(1)在 =λ 的条件下,存在λ使得I为△ABC的内心;a +b +c =0⇔P为△ABC的内心.(2)| |=| |=| |⇔P为△ABC的外心.(3) + + =0⇔G为△ABC的重心.(4) · = · = · ⇔P为△ABC的垂心.考向一求平面向量的夹角例4(2018湖南永州二模,4)已知非零向量a,b的夹角为60°,且|b|=1,|2a-b|=1,则|a|= ()A. B.1C. D.2解析∵非零向量a,b的夹角为60°,且|b|=1,∴a·b=|a|×1× = .∵|2a-b|=1,∴|2a-b|2=4a2-4a·b+b2=4|a|2-2|a|+1=1,∴4|a|2-2|a|=0,∴|a|= (|a|=0舍去),故选A.方法1平面向量的模的求解方法利用向量数量积求解向量的长度问题是向量数量积的重要应用,要掌握此类问题的处理方法:1.a2=a·a=|a|2或|a|= .2.|a±b|= = .3.若a=(x,y),则|a|= 或|a|2=x2+y2.例1已知点A(4,3)和点B(1,2),点O为坐标原点,则| +t |(t∈R)的最小值为 ()A.5 B.5C.3D. 解析由题意可得 =(4,3), =(1,2),∴ +t =(4+t,3+2t),∴| +t |= = = ,∵t∈R,∴当t=-2时,| +t |取得最小值 ,故选D.方法2平面向量夹角的求解方法1.定义法:利用向量数量积的定义知,cosθ= ,其中两个向量的夹角θ∈[0,π],求解时应求出三个量:a·b,|a|,|b|或找出这三个量之间的关系.2.坐标法:若a=(x1,y1),b=(x2,y2),θ为a,b的夹角,则cosθ= .3.三角函数法:可以把所求两向量的夹角放到三角形中,利用正、余弦定理和三角形的面积公式等知识进行求解.例2(2020届江西南昌三校期初调研,6)若非零向量a,b满足|a|= |b|,且(a-b)⊥(3a+2b),则a与b的夹角为 ()A. B. C. D.π解析由(a-b)⊥(3a+2b),得(a-b)·(3a+2b)=0,即3a2-a·b-2b2=0,又知|a|= |b|,∴a·b=3a2-2b2=3× |b|2-2|b|2= |b|2.设a与b的夹角为θ,则cosθ= = = ,又知θ∈[0,π],∴θ= ,即a与b的夹角为 .方法3用向量法解决平面几何问题1.用向量法解决平面几何问题的基本步骤:①建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量的问题;②通过向量运算研究几何元素之间的关系,如距离、夹角等问题;③把运算结果转化成几何关系.2.用向量法解平面几何问题,主要是通过建立平面直角坐标系将问题坐标化,然后利用平面向量的坐标运算求解有关问题,这样可以避免繁杂的逻辑推理,同时加强了数形结合思想在解题中的应用.例3在平行四边形ABCD中,AD=1,∠BAD=60°,E为CD的中点.若 · =1,则AB的长为.解析解法一:由题意可知, = + , =-  + .因为 · =1,所以( + )· =1,即 +  · -  =1. ①因为| |=1,∠BAD=60°,所以 · = | |,因此①式可化为1+ | |- | |2=1.解得| |=0(舍去)或| |= ,所以AB的长为 .解法二:以A为原点,AB所在直线为x轴建立如图所示的直角坐标系,过D作DM⊥AB于点M.由AD=1,∠BAD=60°,可知AM= ,DM= ,∴D .设| |=m(m>