内容提供者
附录A平面图形的几何性质.doc
2024-06-02
10金币
154KB
4页
仙人****88
实名认证
内容提供者
1/4
2/4
3/4
4/4
在线预览结束，喜欢就下载吧，查找使用更方便
相关资料
附录平面图形几何性质.pptx
附录Ⅰ截面的几何性质(AppendixⅠPropertiesofPlaneAreas)三、组合截面的静矩和形心(thefirstmoments¢roidofacompositearea)其中：Ai——第i个简单截面面积例试计算图示三角形截面对于与其底边重合的x轴的静矩。所以§1-2极惯性矩、惯性矩、惯性积(Polarmomentofinertia、Momentofinertia、productofinertia)I=IZ+Iy若截面是高度为h的平行四边形（图b），则其对形心轴x的惯性矩同样为§
2024-01-26
10
767KB
附录A平面图形的几何性质.doc
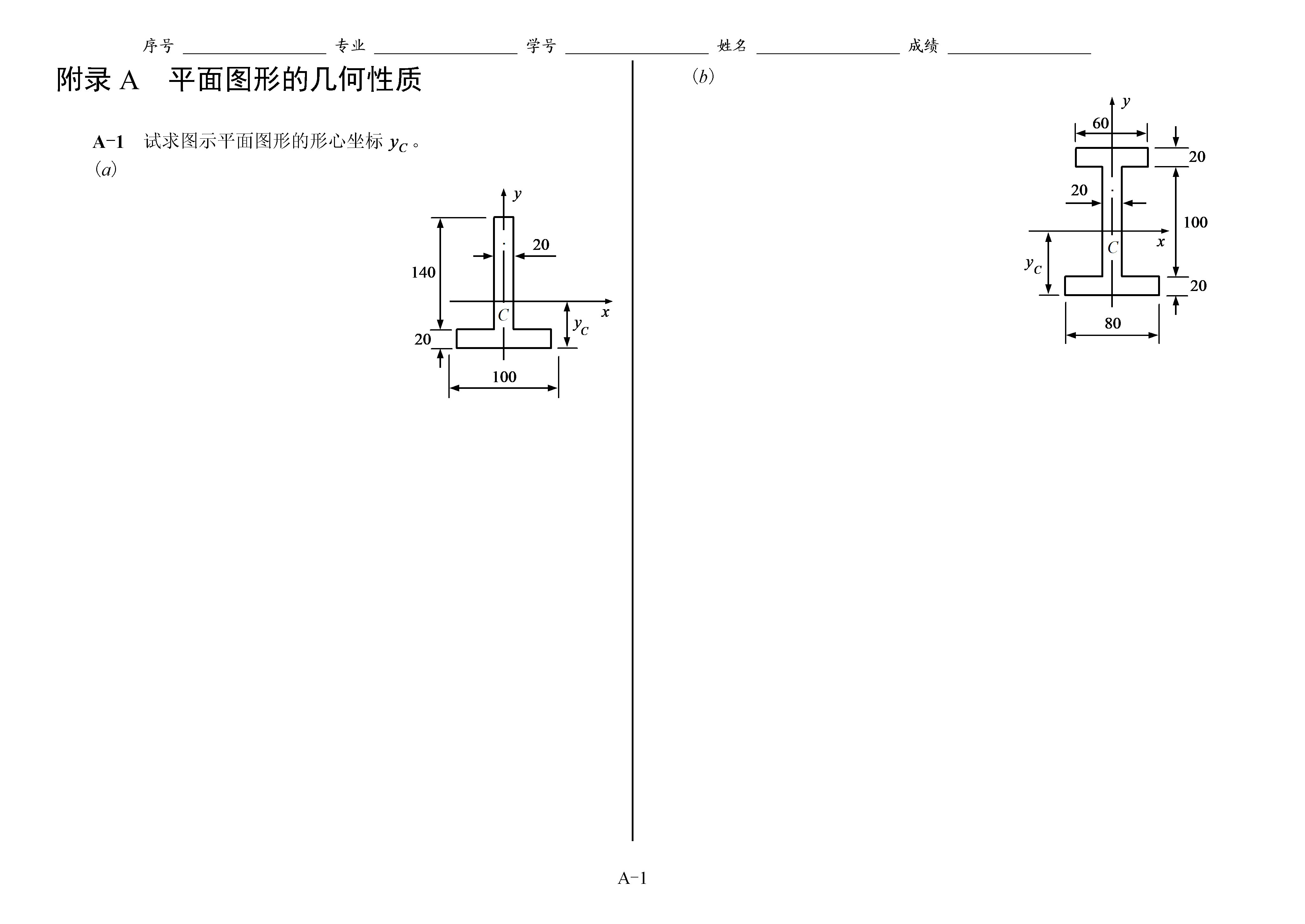
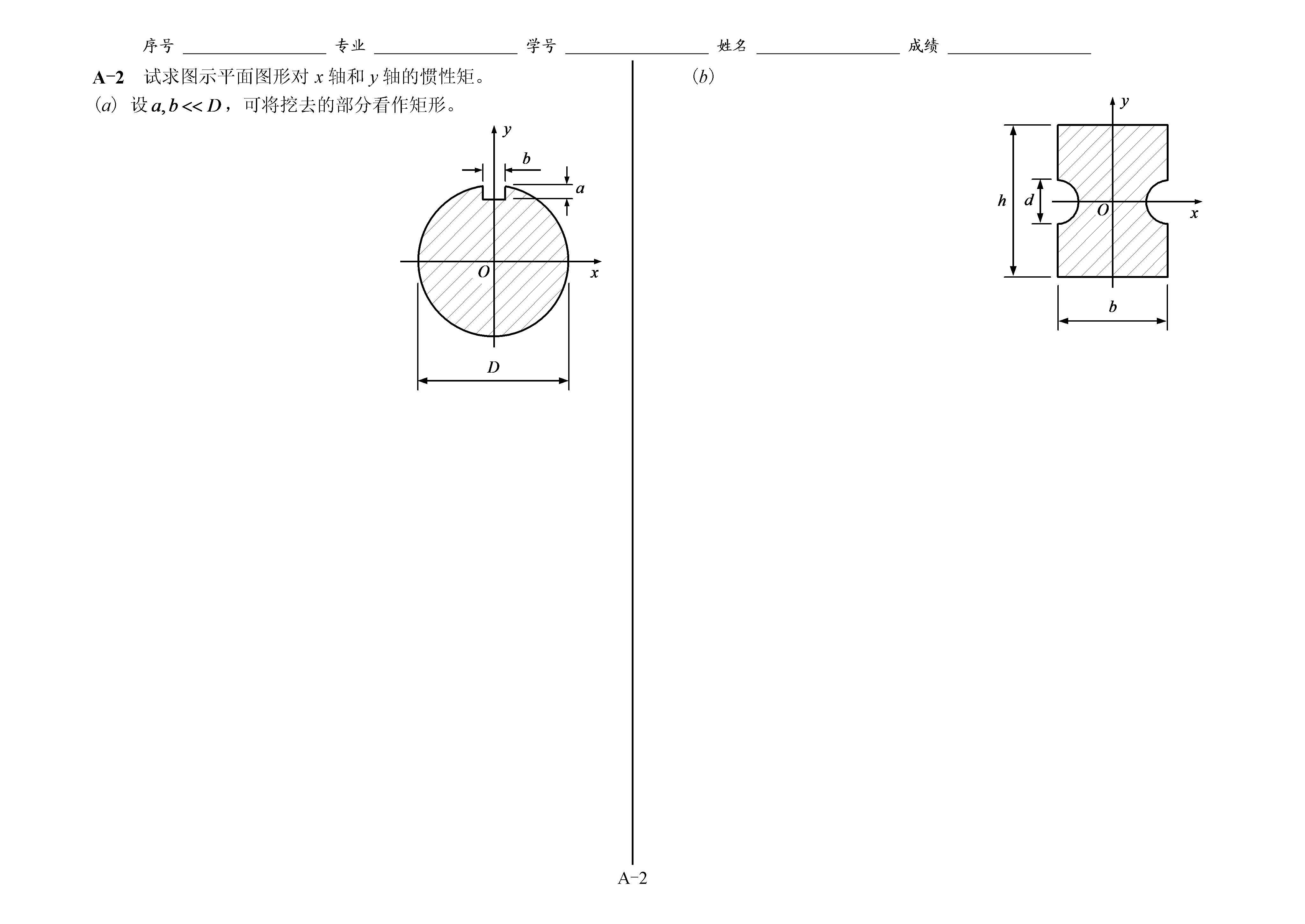
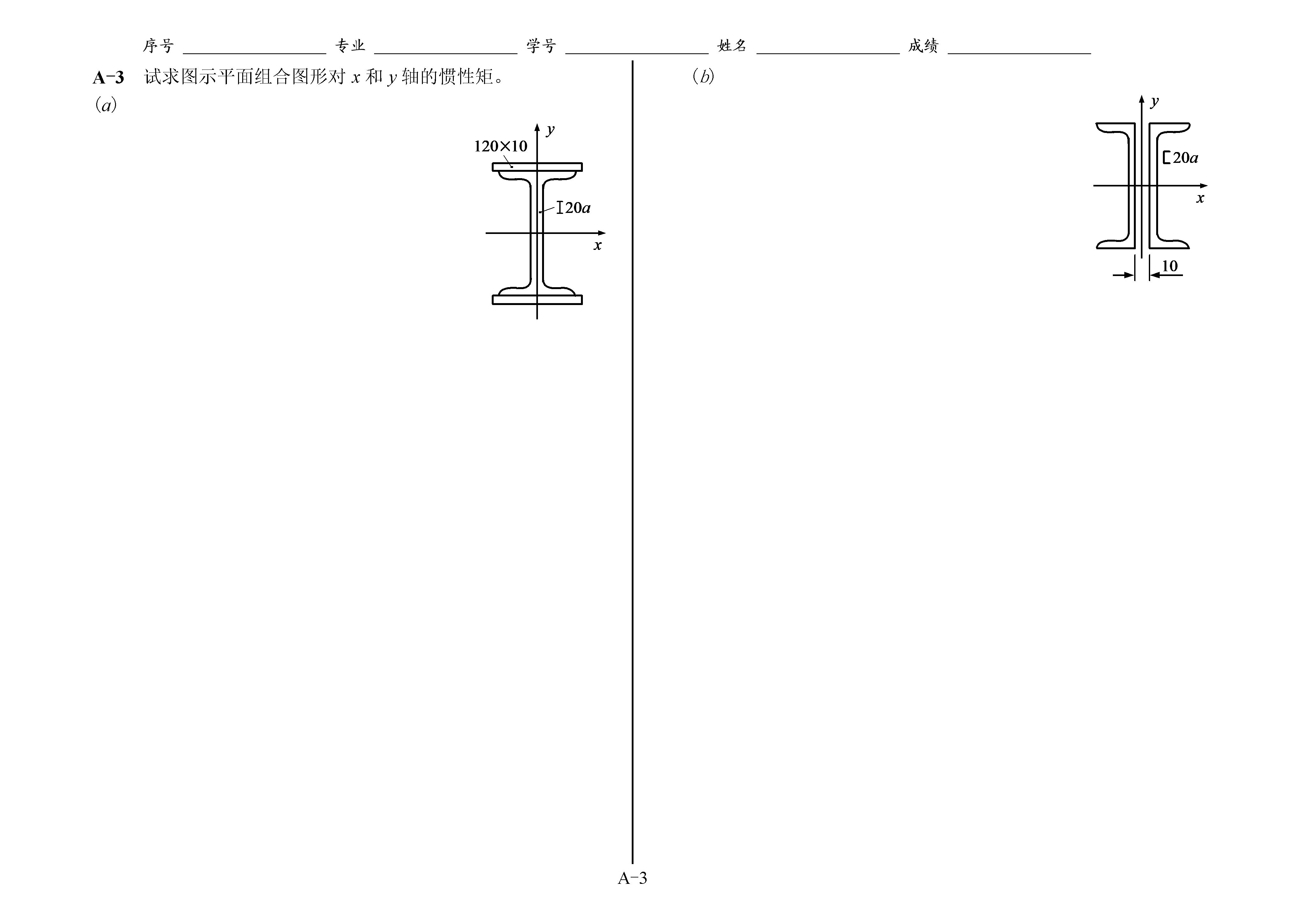
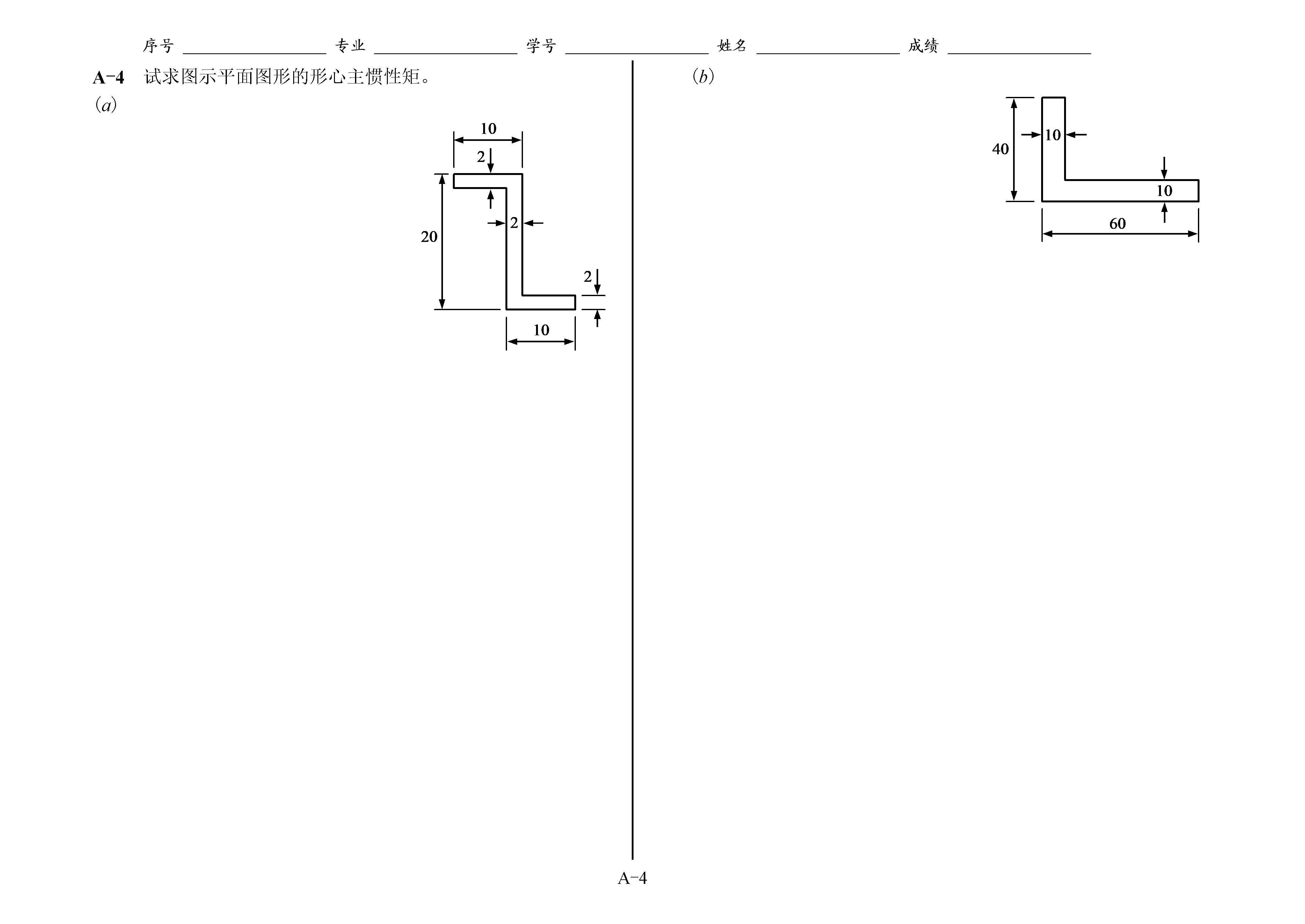
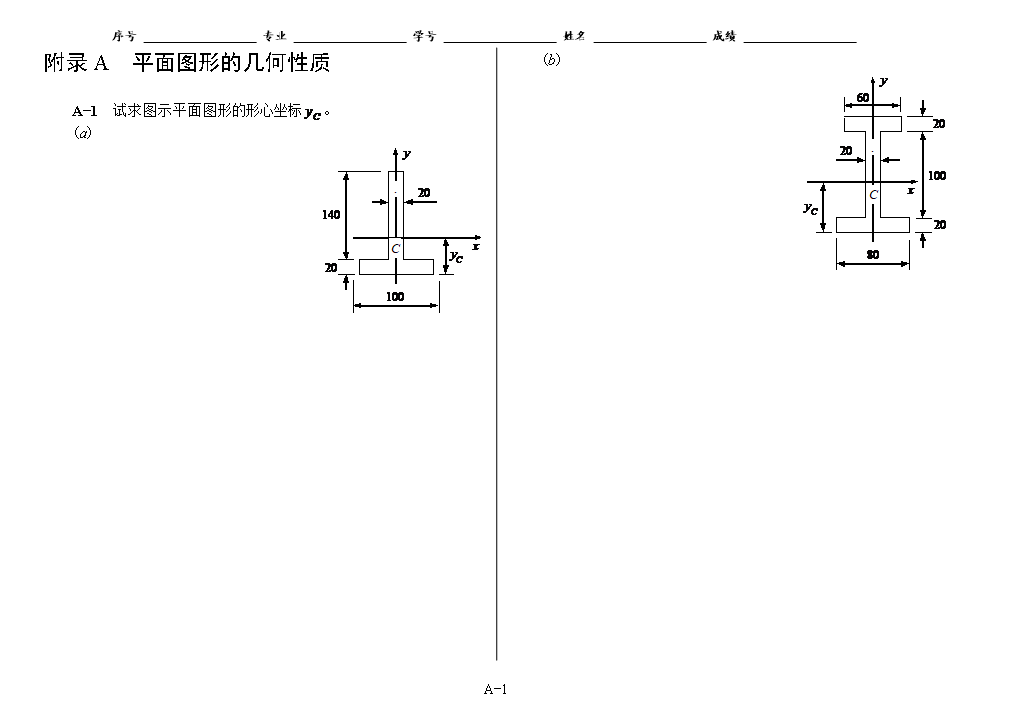
序号专业学号姓名成绩A-4附录A平面图形的几何性质A-1试求图示平面图形的形心坐标。(a)(b)A-2试求图示平面图形对x轴和y轴的惯性矩。(a)设，可将挖去的部分看作矩形。(b)A-3试求图示平面组合图形对x和y轴的惯性矩。(a)(b)A-4试求图示平面图形的形心主惯性矩。(a)(b)
2024-06-02
10
154KB
附录平面图形的几何性质.pptx
例I-1求图示半径为r的半圆形对其直径轴x的静矩及其形心坐标yC。解：将此图形分别为I、II、III三部分，以图形的铅垂对称轴为y轴，过II、III的形心且与y轴垂直的轴线取为x轴，则1.极惯性矩：解：平行x轴取一窄长条，其面积为dA=bdy，则由于圆形对任意直径轴都是对称的，故Ix=Iy注意到Iρ=Ix+Iy，得到一、平行移轴公式例I-5求图示T型截面对形心轴的惯性矩。30一、惯性矩和惯性积的转轴公式③形心主惯性矩：图形对形心主轴的惯性矩；②与主轴方位的对应关系：求a0时只取主值|2a0|≤p/2)，若
2024-01-25
11
383KB
附录Ⅰ平面图形的几何性质.ppt
附录Ⅰ平面图形的几何性质若Sz=0和Sy=0，则yC=0和zC=0。可见，若图形对某轴的静矩等于零，则该轴必通过图形的形心；反之，若某轴通过图形的形心，则图形对该轴的静矩必等于零。当一个平面图形是由若干个简单图形（例如矩形、圆形、三角形等）组成时，根据静矩的定义，组合图形对某轴的静矩应等于其各组成部分对该轴静矩之和，解:取平行于z轴的狭长条作为微面积dA，则例Ⅰ-2确定图Ⅰ-3所示L形平面图形的形心C的位置。解:将图形看作是由两个矩形Ⅰ和Ⅱ组成的，选取坐标系如图所示，每一矩形的面积和形心坐标分别为第二节惯
2024-03-01
9
201KB
附录A 平面图形的几何性质b.ppt
附录A平面图形的几何性质第一节静面矩和形心第一节静面矩和形心4、静面矩的值可以是正值、负值、或零。⑵图形对过形心轴的静面矩为零，反之图形对某轴的静面矩为零，则此轴一定过图形的形心。2、形心确定的规律：例试确定下图的形心。图（b）解：1）负面积法例：如图所示，求绿色图形对Z、Y轴的静面矩及图形的形心。第二节惯性矩、惯性积6、轴惯性矩与极惯性矩的关系：b二、惯性半径：解：二、组合图形的惯性矩、惯性积：200附录A平面图形的几何性质z（矩形的对称轴）第四节转轴公式附录A平面图形的几何性质二、分析2、主惯性矩：5
2024-10-23
16
918KB