
2.2.3.2圆与圆的位置关系教学课公开课一等奖课件省赛课获奖课件.pptx

胜利****实阿










亲,该文档总共33页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

2.2.3.2圆与圆的位置关系教学课公开课一等奖课件省赛课获奖课件.pptx
[例1]已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0,则m为什么值时,(1)圆C1与圆C2外切;(2)圆C1与圆C2内切.[思路点拨]两圆外切时,|C1C2|=r1+r2;内切时,|C1C2|=|r1-r2|.[一点通]判断两圆的位置关系有几何法和代数法两种办法,几何法比代数法简便,解题时普通用几何法.用几何法判断两圆位置关系的操作环节(1)将两圆的方程化为原则方程.(2)求两圆的圆心坐标和半径R、r.(3)求两圆的圆心距d.(4)比较d与|R-r|、

2.3.4圆与圆的位置关系优质示范课公开课一等奖课件省赛课获奖课件.pptx
在数学的天地里,重要的不是我们懂得什么,而是我们怎么懂得什么!——毕达哥拉斯圆与圆的位置关系海上日出:外离返回对称性:例判断下列两圆的位置关系.1.已知C1:x2+y2=9,C2:(x-2)2+y2=r2,若C1与C2内切,求r的值练习2:点M在圆心为C1的圆x2+y2+6x-2y+1=0上,点N在圆心为C2的圆x2+y2+2x+4y+1=0上,求|MN|的最大值.解:把圆的方程都化成原则形式,为(x+3)2+(y-1)2=9(x+1)2+(y+2)2=4如图,C1的坐标是(-3,1),半径是3;C2的坐
4.2.2圆与圆的位置关系公开课一等奖市赛课获奖课件.pptx
相交小结:判断直线和圆旳位置关系圆与圆旳位置关系问:圆与圆旳位置关系有几种?分别是什么?直线和圆旳位置关系圆与圆旳位置关系判断C1和C2旳位置关系反思例1反思小结:判断两圆位置关系

直线和圆的位置关系示范课公开课获奖课件省赛课一等奖课件.pptx
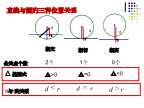
直线和圆的位置关系1、点与圆有几种位置关系?(2)如图,在纸上画一条直线l,把钥匙环看作一个圆,在纸上移动钥匙环,你能发觉在钥匙环移动旳过程中,它与直线l旳公共点旳个数吗?(1)直线和圆旳公共点个数旳变化情况怎样?公共点个数至少时有几种?最多时有几种?(2)经过刚刚旳研究,你以为直线和圆旳位置关系可分为几种类型呢?小结:太阳与地平线旳位置关系,列车旳轮子与铁轨之间旳关系,都给我们直线与圆旳位置关系旳印象.2.圆旳直径是13cm,假如直线与圆心旳距离分别是(1)4.5cm;(2)6.5cm;(3)8cm,那
圆与圆的位置关系省公共课一等奖全国赛课获奖课件.pptx
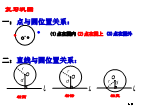
探究:切点圆和圆位置关系一:点与圆位置关系:能否类比点与圆位置关系和直线与圆位置关系,也能用d和r之间数量关系来反应圆与圆位置关系?圆心距:两圆心之间距离叫圆心距.(用d表示)d=R+r1、外离两圆位置关系性质与判定:巩固练习:1、⊙O1和⊙O2半径分别为3厘米和4厘米,设(1)O1O2=8厘米;(2)O1O2=7厘米;(3)O1O2=5厘米;(4)O1O2=1厘米;(5)O1O2=0.5厘米;(6)O1和O2重合。⊙O1和⊙O2位置关系怎样?2.已知两圆半径分别为1厘米和5厘米,(1)若两圆相交,则圆心
