
高数-微分方程-高阶常系数非齐次线性方程的特解.pdf

文库****品店







亲,该文档总共52页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

高数-微分方程-高阶常系数非齐次线性方程的特解.pdf
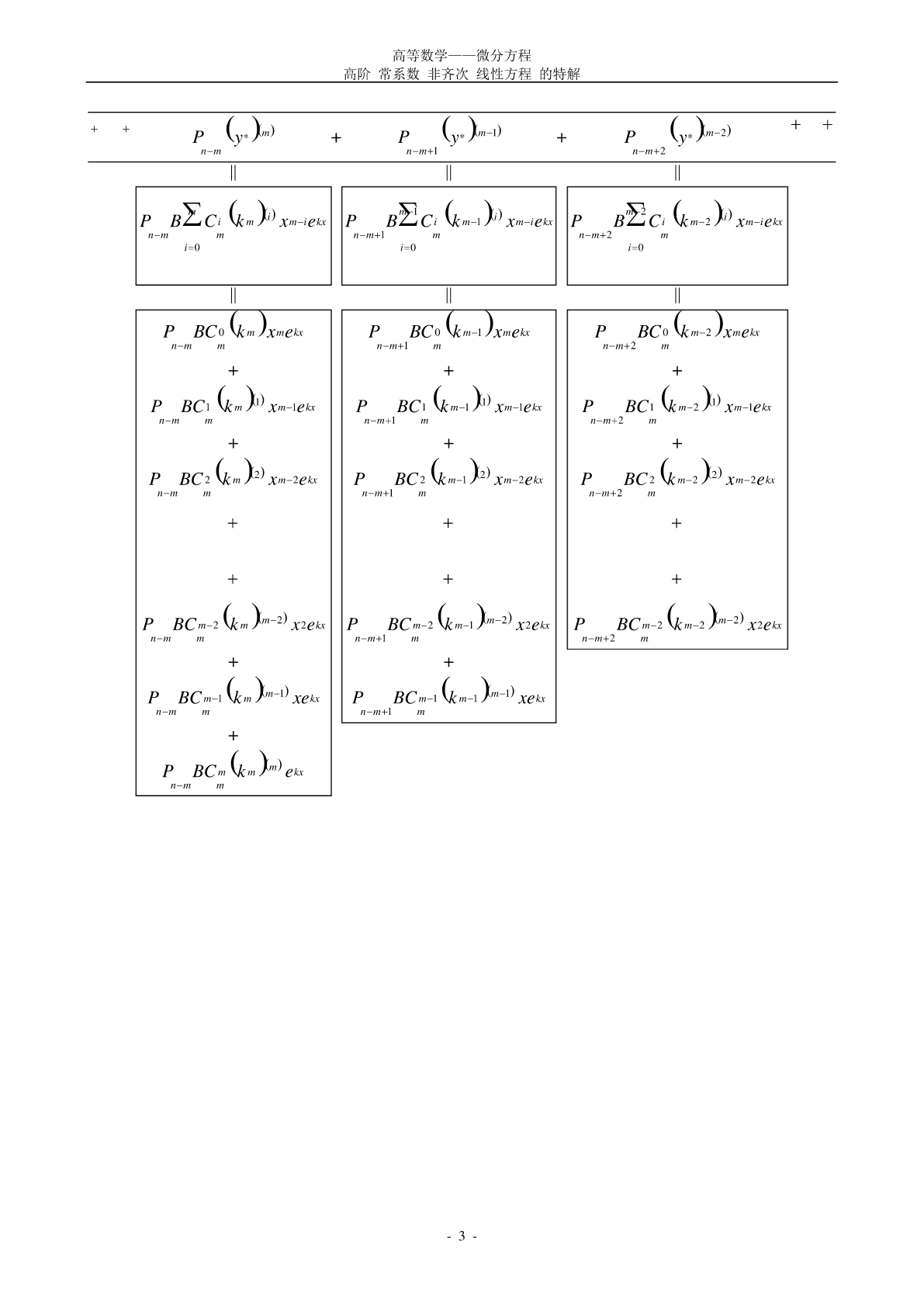
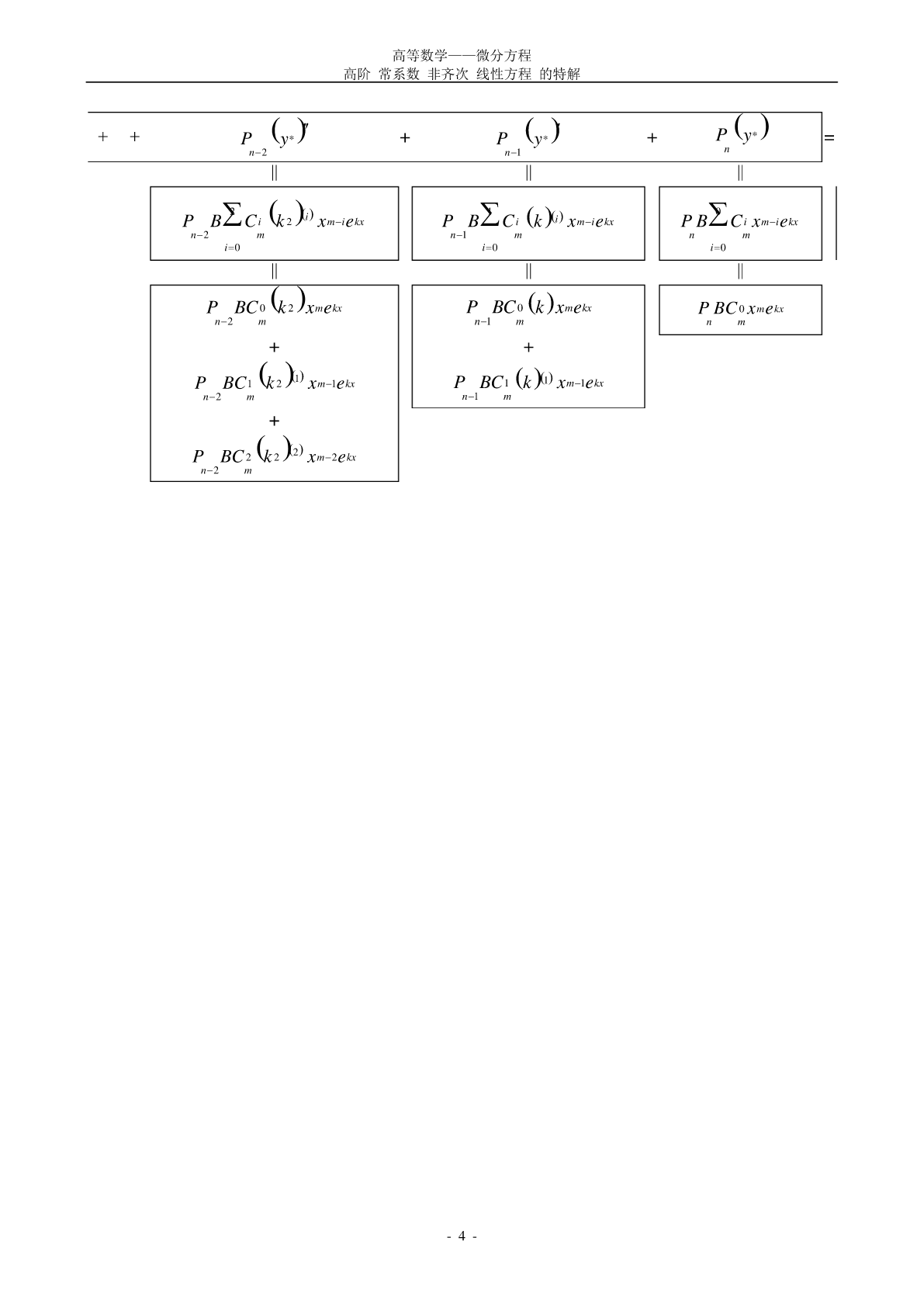
高等数学——微分方程高阶常系数非齐次线性方程的特解2010年8月~10月解读《2010版考研数学复习指南(理工类,文登考研培训特供版)》P160,表6-6------------------------------------------------------------------------------------------------------------------------1.原方程为ynPyn1Pyn2PyPyekx....................

高数-微分方程-高阶常系数非齐次线性方程的特解.pdf
高等数学——微分方程高阶常系数非齐次线性方程的特解2010年8月~10月解读《2010版考研数学复习指南(理工类,文登考研培训特供版)》P160,表6-6------------------------------------------------------------------------------------------------------------------------1.原方程为ynPyn1Pyn2PyPyekx....................

高数常系数非齐次线性微分方程课件.pptx
会计学10/23/202410/23/202410/23/202410/23/202410/23/202410/23/202410/23/202410/23/202410/23/202410/23/202410/23/202410/23/202410/23/202410/23/202410/23/202410/23/202410/23/202410/23/2024

常系数高阶齐次线性微分方程.ppt
高阶常系数齐次线性方程一、定义n阶常系数线性微分方程的标准形式二、二阶常系数齐次线性方程解法1.有两个不相等的实根2.有两个相等的实根3.有一对共轭复根定义解三、n阶常系数齐次线性方程解法注意特征根为四、小结思考题思考题解答练习题练习题答案微分方程的应用题例1.某种飞机在机场降落时,为了减少滑行距离,在触地的瞬间,飞机尾部张开减速伞,以增大阻力,使飞机迅速减速并停下.现有一质量为9000kg的飞机,着陆时的水平速度为700km/h.经测试,减速伞打开后,飞机所受的总阻力与飞机的速度成正比(比例系数为问从着

微分算子法求解二阶常系数非齐次线性微分方程的特解.doc
微分算子法求解二阶常系数非齐次线性微分方程的特解李绍刚段复建徐安农(桂林电子科技大学,计算科学与数学系,广西桂林,541004)摘要:本文主要介绍了二阶微分算子的性质及其它在一些求解二阶常系数非齐次线性微分方程的常见运算公式,并对其中的大部分重要公式给出了详细的较为简单的证明,并通过具体而翔实的例子加以说明它在解题中的具体应用,大大简化了二阶常系数非齐次线性微分方程的特解的求法。关键词:线性微分算子非齐次微分方程特解中图分类号:O175.1引言对于微分方程,尤其是常系数非齐次线性微分方程,算子法求其特解一
