课件-全国-2010_中考数学复习 《分类讨论》课件 苏教版.rar

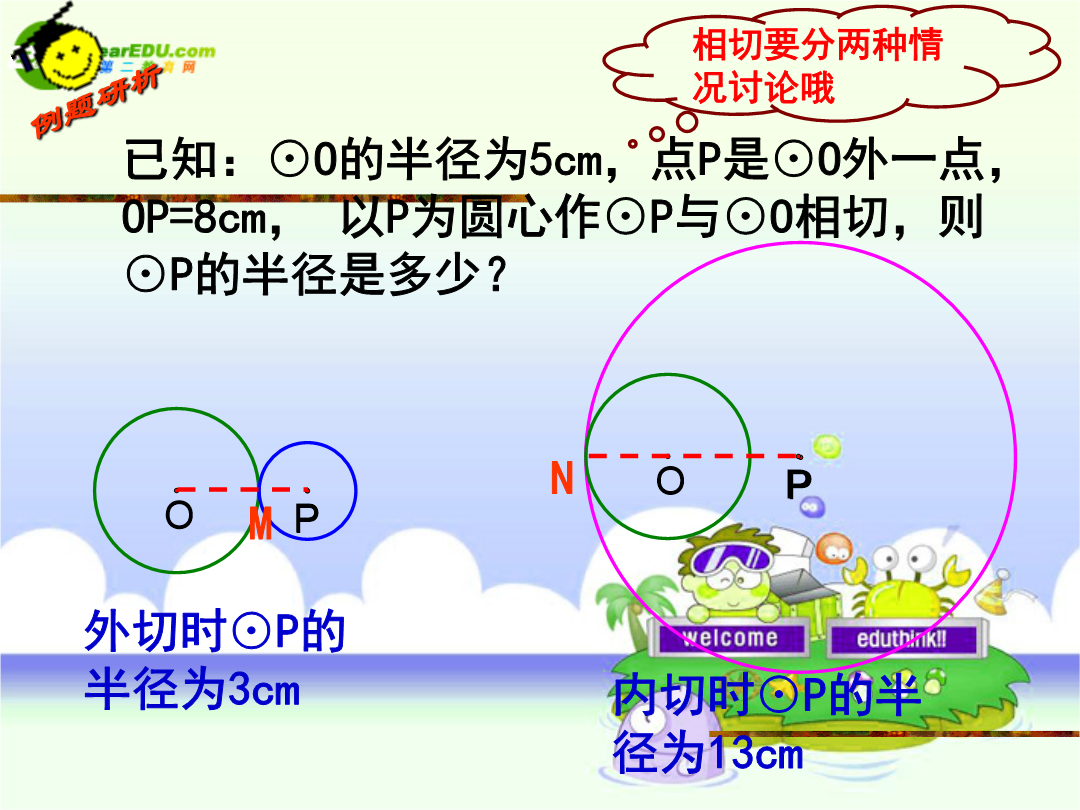
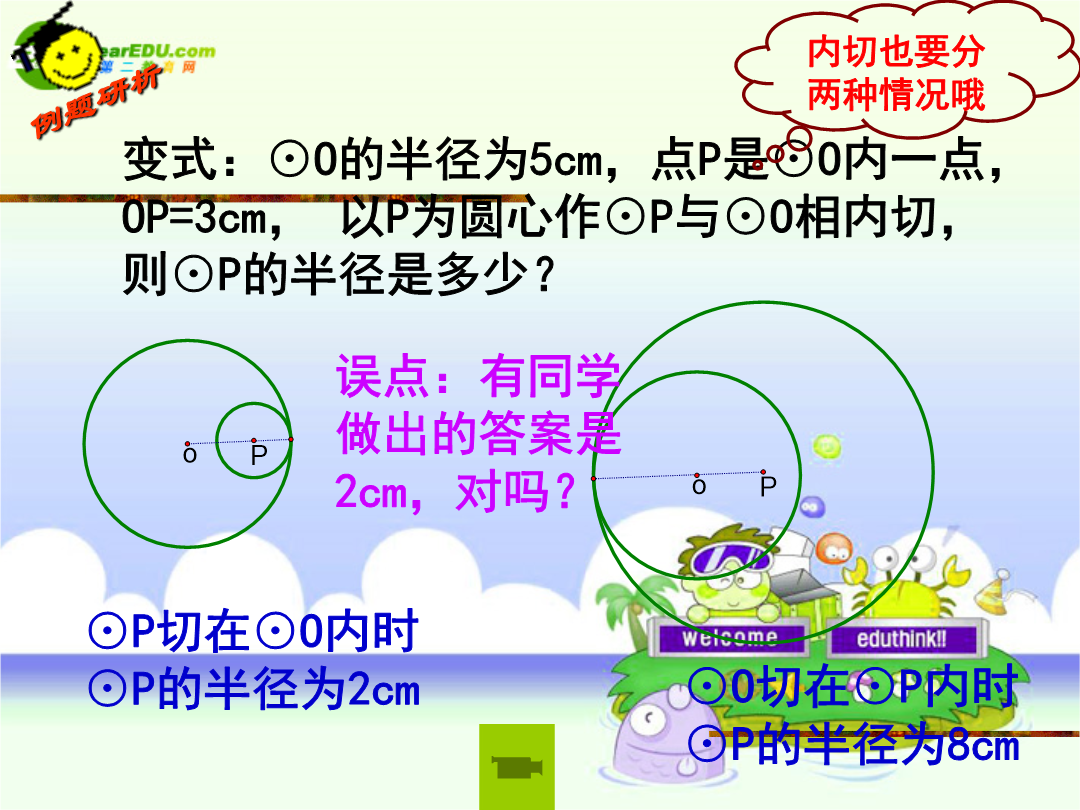
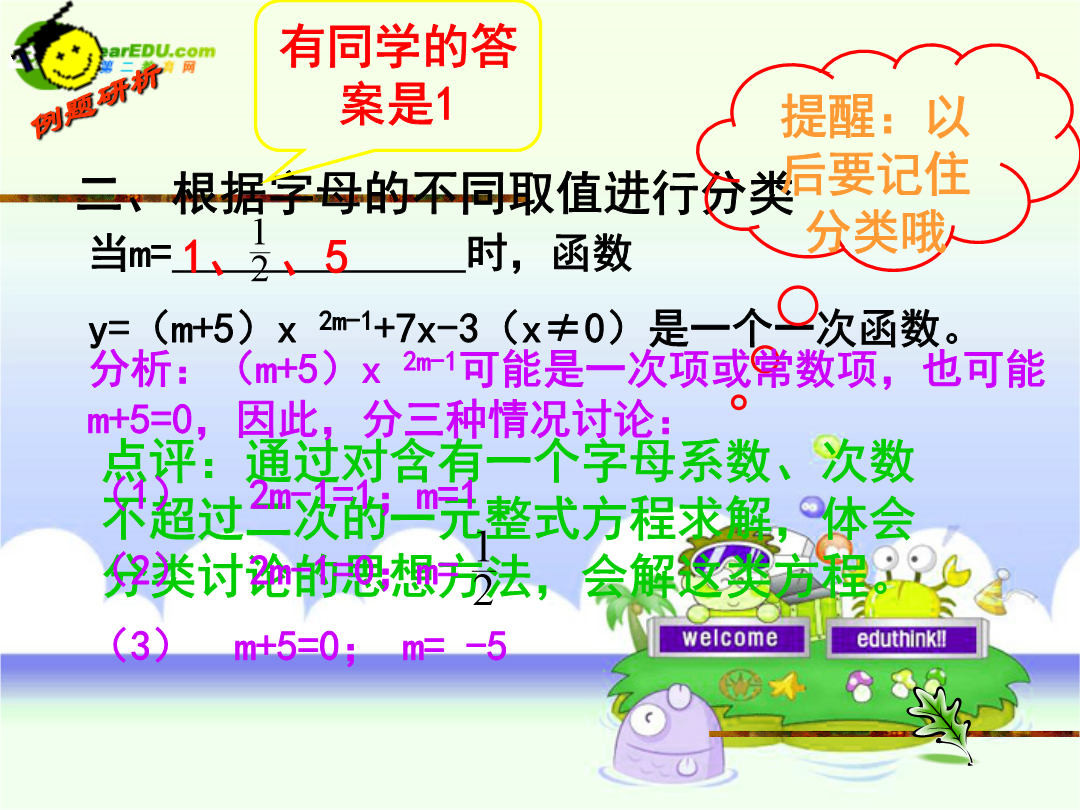
数学复习专题----分类讨论学习目标1、了解“分类讨论”的基本思想，会用“分类讨论”思想解决简单的数学问题一、根据某些数学概念的定义进行分类已知：⊙O的半径为5cm，点P是⊙O外一点，OP=8cm，以P为圆心作⊙P与⊙O相切，则⊙P的半径是多少？变式：⊙O的半径为5cm，点P是⊙O内一点，OP=3cm，以P为圆心作⊙P与⊙O相内切，则⊙P的半径是多少？及时反馈1二、根据字母的不同取值进行分类及时反馈2三、根据某些定理或公式的限制条件进行分类已知：等腰三角形的一条腰上的高等于该三角形某一条边的长度的一半，则其顶角为．解2：当高BD在三角形外部且是腰AB的一半时∵在RT△ABD中，BD=AB∴∠DAB=30°∴∠BAC=150°解3：当高BD是底BC的一半时∵在RT△CBD中，BD=BC∴∠C=30°∴∠BAC=120°三、根据某些定理或公式的限制条件进行分类1、直角三角形的两条边长分别为6和8,那么这个三角形的外接圆半径等于.四、根据运算性质的适用范围或运算的特殊规定而分类及时反馈4五、根据图形的位置变化进行分类讨论已知⊙Ｏ的半径为５ｃｍ，弦ＡＢ∥ＣＤ，ＣＤ＝６ｃｍ，ＡＢ＝８ｃｍ，求ＡＢ和ＣＤ的距离。解：连接OA、OC，过点O作OE⊥CD交CD于点E，并延长EO交AB于点F∵OE⊥CD∴CE=DE=3又∵ＡＢ∥ＣＤ，OE⊥CD∴OF⊥AB∴AF=BF=4∵在RT△OCE中，OC=5，CE=3∴OE=4同理OF=3∴EF=OE+OF=4+3=7即ＡＢ和ＣＤ的距离为7五、根据图形的位置变化进行分类讨论及时反馈5及时反馈5及时反馈5归纳小结一路下来，我们共同回顾了所学知识，又解决了一些问题，你一定有很多收获，希望你能与同学、与父母分享。