
数值分析计算实习题.docx

胜利****实阿









亲,该文档总共17页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

数值分析计算实习题.docx
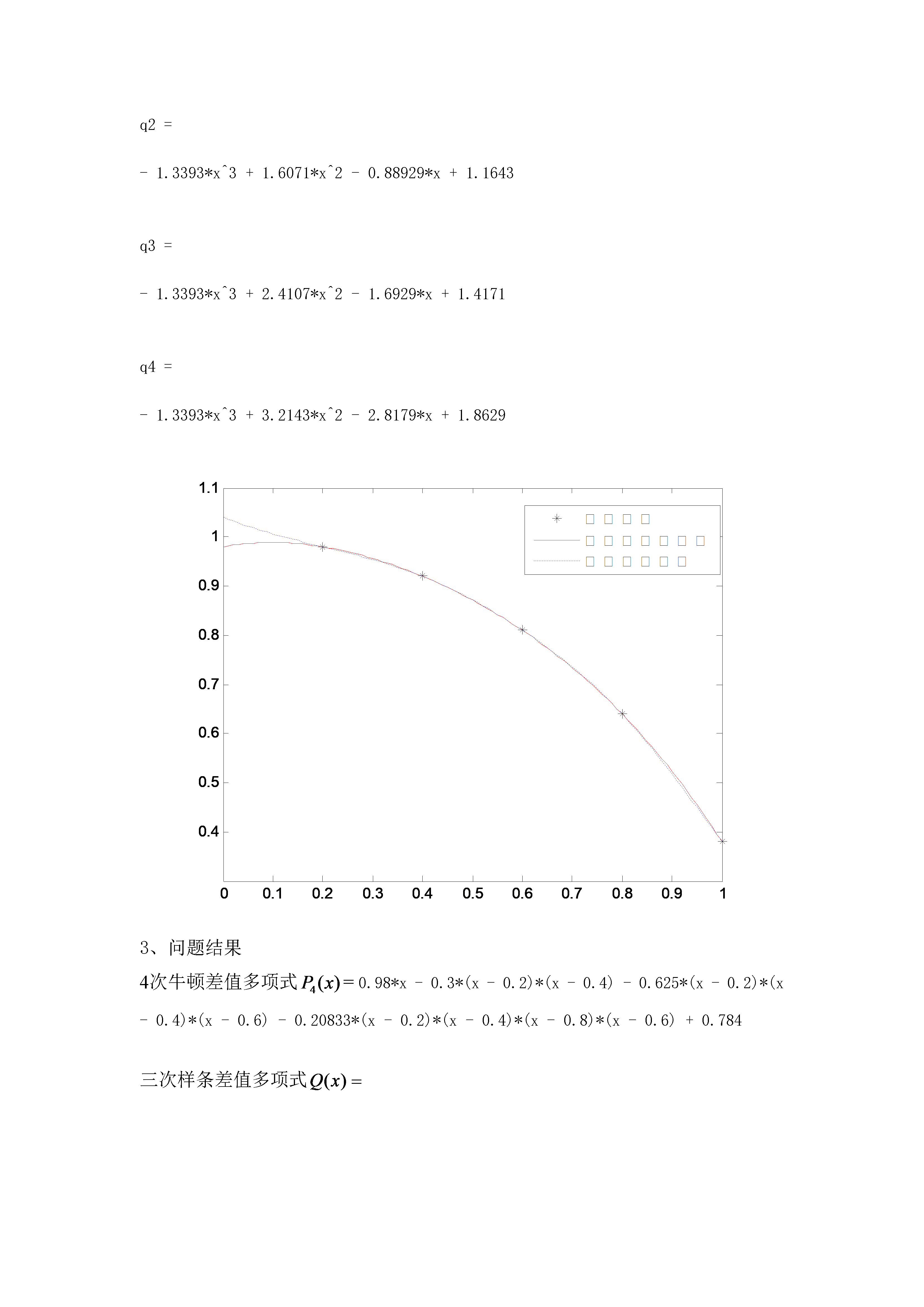
《数值分析》计算实习题姓名:学号:班级:第二章1、程序代码Clear;clc;x1=[0.20.40.60.81.0];y1=[0.980.920.810.640.38];n=length(y1);c=y1(:);forj=2:n%求差商fori=n:-1:jc(i)=(c(i)-c(i-1))/(x1(i)-x1(i-j+1));endendsymsxdfd;df(1)=1;d(1)=y1(1);fori=2:n%求牛顿差值多项式df(i)=df(i-1)*(x-x1(i-1));d(i)=c(i-1)

数值分析计算实习题.pdf
插值法1.下列数据点的插值x01491625364964y012345678可以得到平方根函数的近似,在区间[0,64]上作图.(1)用这9个点作8次多项式插值Ls(x).(2)用三次样条(第一边界条件)程序求S(x).从得到结果看在[0,64]上,哪个插值更精确;在区间[0,1]上,两种插值哪个更精确?解:(1)拉格朗日插值多项式,求解程序如下symsxl;x1=[01491625364964];y1=[012345678];n=length(x1);Ls=sym(0);fori=1:nl=sym(y1

数值分析计算实习题.docx
插值法下列数据点的插值x01491625364964y012345678可以得到平方根函数的近似,在区间[0,64]上作图.(1)用这9个点作8次多项式插值Ls(x).(2)用三次样条(第一边界条件)程序求S(x).从得到结果看在[0,64]上,哪个插值更精确;在区间[0,1]上,两种插值哪个更精确?解:(1)拉格朗日插值多项式,求解程序如下symsxl;x1=[01491625364964];y1=[012345678];n=length(x1);Ls=sym(0);fori=1:nl=sym(y1(i

数值分析计算实习题.docx
《数值分析》计算实习题姓名:学号:班级:第二章1、程序代码Clear;clc;x1=[0.20.40.60.81.0];y1=[0.980.920.810.640.38];n=length(y1);c=y1(:);forj=2:n%求差商fori=n:-1:jc(i)=(c(i)-c(i-1))/(x1(i)-x1(i-j+1));endendsymsxdfd;df(1)=1;d(1)=y1(1);fori=2:n%求牛顿差值多项式df(i)=df(i-1)*(x-x1(i-1));d(i)=c(i-1)

数值分析第二章计算实习题.doc
%对龙格函数:的三次样条插值.clear;x0=-1:0.1:1;y0=1./(25*x0.^2);x1=linspace(-1,1,20);y1=interp1(x0,y0,x1,'spline');plot(x0,y0,'b');holdonplot(x1,y1,'m');title('三次样条插值','FontName','TimesNewRoman','FontSize',11);legend('龙格函数曲线','三次样条插值曲线',-2);axis([-1,1,0,1]);xlabel('x轴'
