非球面轮廓测量与分析.ppt

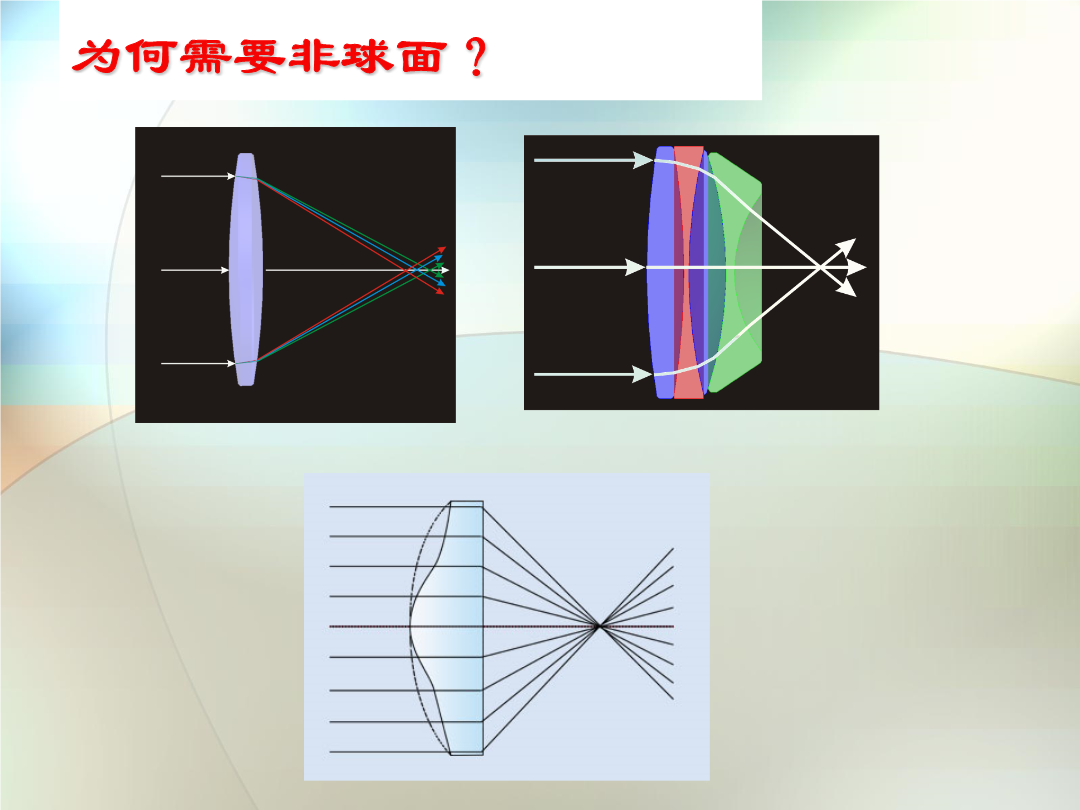
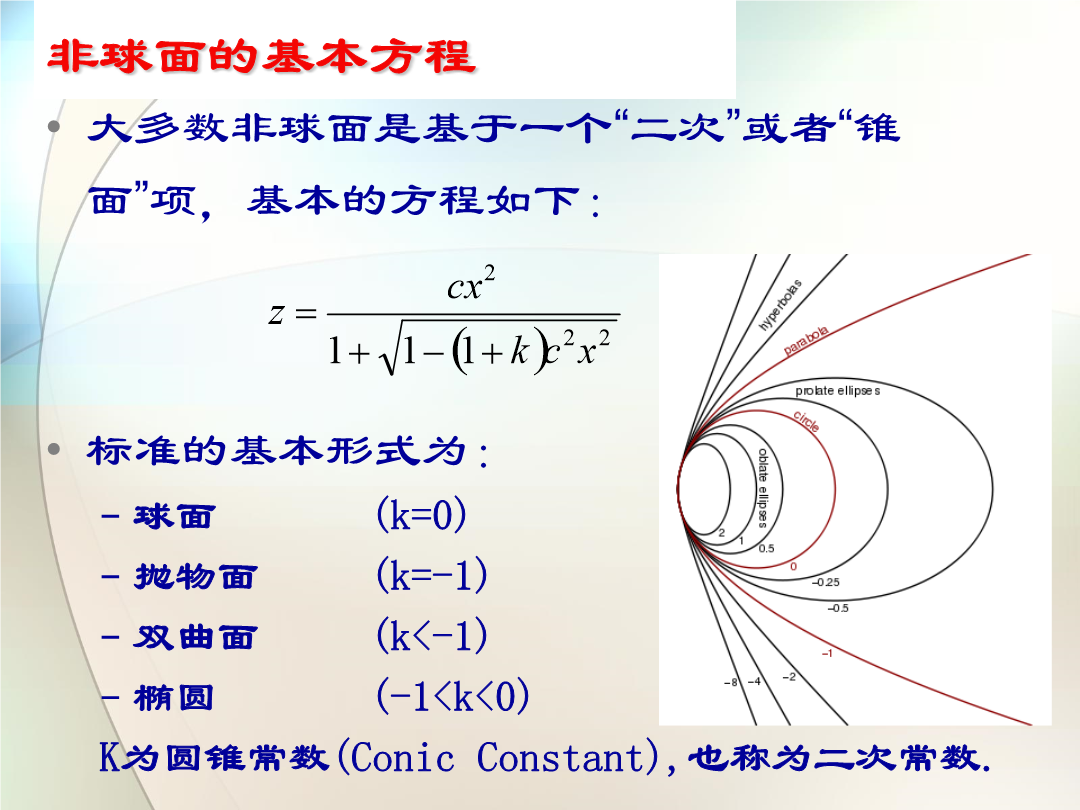
非球面轮廓测量与分析主要内容非球面简介概况什么是非球面？为何需要非球面？使色差最小有效减少光学系统中的透镜个数降低光学系统的重量降低总成本专门的设计可以产生2个或更多的焦点(例如DVD透镜)非球面的典型应用大多数非球面是基于一个“二次”或者“锥面”项，基本的方程如下：标准的基本形式为：球面(k=0)抛物面(k=-1)双曲面(k<-1)椭圆(-1<k<0)K为圆锥常数(ConicConstant),也称为二次常数.圆锥常数(Conicconstant)之所以称为“锥面”项，是由于我们可以用不同方位的面与圆锥相切可以得到以上表面相切面平行于圆锥底面相切面平行于圆锥侧面相切面平行于圆锥轴线相切面与圆锥轴线成某一角度基本项(二次项)非球面公式比较偶次非球面与奇次非球面金刚石车削和铣磨单点或接近单点接触精度取决于位置控制模具成型几何反转精度取决于：模具的几何精度收缩因素抛光抛光垫接触或者MRF(磁流体)精度取决于局部驻留时间典型加工时间(50mm口径)<10分钟典型形状精度0.1µm至1µm材料有色金属，如铝、铜、镍等晶体，如锗、硫化锌、硅、铌酸锂等高分子聚合物刀具刀尖的形状误差将会被复制到工件的表面上许多用户从未想过用FTS去检查刀具的半径和形状误差对于非球面，误差平行于非球面轴对于球面，误差沿最佳拟合圆的法向非球面轮廓测量方法简介非球面測定非球面測定方式FormTalysurf测量非球面FormTalysurf测量非球面cx2AsphericData非球面数据Radius=40.0mmK=-1A4=5.3188e-007A6=5.5231e-009A8=-1.6774e-011A10=-6.3352e-014XAxis+Z轴7)AnalysisResults分析结果非球面参数简介非球面参数简介非球面参数简介非球面参数简介非球面参数简介非球面参数简介非球面参数简介非球面参数简介非球面参数简介非球面参数简介非球面参数简介Wellknowntoopticsuserbase光学用户都非常熟知StylusFlanking测头侧面接触PGI850&1250-MeasurementMethod测量方法Level1(StandardforPGI635)BasicFormAnalysis基本的形状分析RadiusOptimisation半径优化Cursors/Exclusions光标操作Lambda‘S’Filterλs滤波Level2(StandardforPGI840&PGI1240)AstigmatismAnalysis对称性分析SAGTableAnalysisSAG表分析Level3(StandardforPGI850&PGI1250)DerivedCoefficientAnalysis得到非球面系数(逆向)DataCursor光标AsphericCoefficientStorage非球面参数的存储及调入Waviness(λs)Filter波纹度(λs)滤波AstigmatismAnalysis对称性分析AstigmatismAnalysis对称性分析AstigmatismAnalysis对称性分析AstigmatismAnalysis对称性分析SAGTableAnalysisSAG表格分析NominalRadiusResult名义基圆半径时的结果OptimisedRadiusResults最佳基圆半径时的形状误差分析结果DerivedCoefficientsFunction得到非球面系数(逆向)实际机种面型分析实际机种面型分析实际机种面型分析实际面型As分析实际面型As分析实际面型误差分析讨论:谢谢您的聆听！