数学物理方法概论课件市公开课一等奖百校联赛特等奖课件.pptx

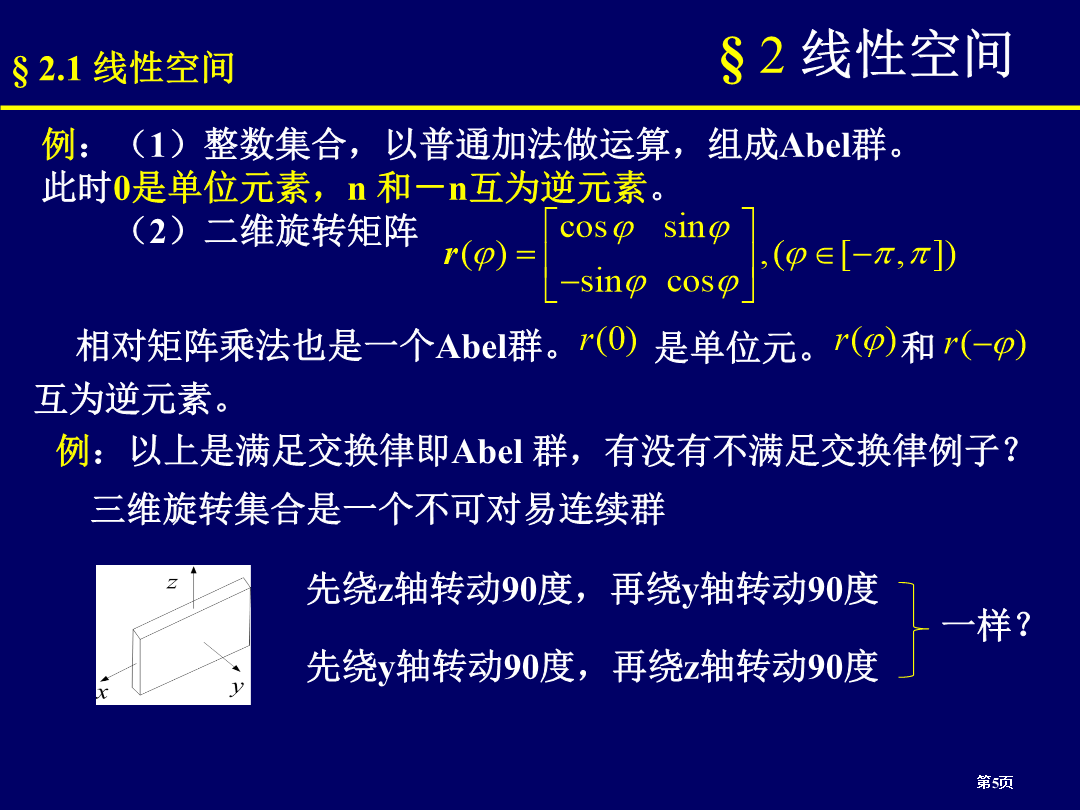
数学物理方法概论第二章线性空间1、线性空间；2、线性变换；3、线性变换本征值与本征向量；4、内积空间；5、正交化法；6、自伴算子；7、等距变换；8、正规变换本征值与本征向量；9、平方可积函数空间；10、完备正交归一函数集；11、多项式迫近12、完备正交归一集例子；13、正交多项式§2线性空间§2线性空间§2线性空间§2线性空间§2线性空间§2线性空间§2线性空间§2线性空间§2线性空间§2线性空间§2线性空间§2线性空间§2线性空间§2线性空间五、线性空间基与维数基：指线性空间V中最大线性无关子集。V中任一向量均可由这个子集中向量线性组合表示。维数：基中所含向量数目，称为空间维数。§2线性空间六、线性空间同构（A）映射定义：设S1和S2是两个非空集合，假如按照一定法则f，对于S1中每个元素x，都存在S2中一个确定元素y与之对应，则称f为定义在S1上取值于S2中一个映射，记为，y称为x在映射f下像。（B）线性空间同构设S=｛E,*｝和S′=｛E′,·｝是分别含有封闭运算*和·代数系统，假设f是一个从E到E′双射，即一一映射，它给每个属于E元a，b，c，…∈E，都有指定属于E′元，f（a），f（b），f（c），…∈E′，与之对应线性空间同构判定方法：设U和V是同一数域F上两个线性空间，f是从U到V一个映射，假如:（1）f是一个双射；（2）f是一个线性映射，即则称f是U到V同构映射，并说U与V同构。定理：域F上每一个n维线性空间都和空间同构。§2线性空间§2线性空间§2线性空间定义：指在线性空间V(F)中变换A,对每一个有确定向量，且对任意有则称A为线性变换也称线性算子。式中a，b为标量§2.2线性变换§2.2线性变换§2.2线性变换§2.2线性变换三、线性变换逆变换：四、线性变换矩阵表示：定理2：设是一组基，是中任意n个向量，则存在唯一线性变换A，使例：求F[x]n求导变换，在基1，x，x2，…,xn-1下矩阵。定理4：同一线性变换在不一样基下对应矩阵是相同。即：若存在可逆矩阵A，使矩阵B和C满足则称B和C是相同矩阵。记例：设A是一个实三维空间上旋转变换，它把空间任一矢量绕轴右旋一个角度,求此变换在Cartesian基下矩阵。定义：设A是V(F)上线性变换，假如则称为A本征值，为A属于本征向量。即：(1)线性变换A本征值集合称为A谱，其中本征值模最大值称为谱半径。(2)若是A本征多项式k级零点，则说该本征值代数重数为k。当时称A谱是简并。(3)假如变换A有n个线性无关本征向量（n为空间维数），则它矩阵一定能够经过相同变换对角化，且对角元素为A本征值。例：以下矩阵是否与对角矩阵相同秩：，所以属于线性无关特征向量只有在实三维空间，普通向量长度和两向量夹角是经过标积定义，假如则：§2.4内积空间二、向量范数、内积和范数性质：证实:(1)由内积公理第一条知定理2：（施瓦兹Schwartz不等式）若x,y是复内积空间中任一对向量，则三、正交性和完备性定理1：正交归一集是线性无关集。（即在n维空间中任何n个向量正交归一集都能够作为该空间基）定理2：（Bessel不等式）设是内积空间任一有限正交归一集，x为空间任一向量，则以下几个相关有限维内积空间正交归一集完备性说法等价：一、度量矩阵说明：（1）度量矩阵是厄米正定矩阵。因为满足（2）度量矩阵在实空间是个正定矩阵。（3）度量矩阵与基选择相关。最简单度量矩阵就是单位矩阵，对应基就是正交归一基。即度量矩阵能够经过选择一组正交归一基转化为单位矩阵。（4）定义正交归一基方法：葛兰姆－施密特正交化方法。例：设空间中一组基：类似地，定义：已知A是内积空间上线性变换，假如对任意，变换满足则称为A伴随算子。几点说明：（1）对给定线性算子，其对应伴随算子是唯一，且是线性。（2）A和在同一基下矩阵间关系（3）在正交基下，G是单位矩阵，则有二、自伴算子3、判定定理：定理1：若A是实内积空间上自伴算子，则对任意，有充要条件是定理2：若A是酉空间上线性变换，则对全部，充要条件是。例：给定g(x),求在区间中满足注意内积要求不惟一，在上式积分中加上w(x)>0权重数也是可采取内积。不过伴随算子依赖于内积，所以能够选定内积，使其成为自伴算子。依据定义，先结构伴随算子左边，有则第二个边界项也为零。显然，对于由式确定内积，从伴随算子定义式知，伴随算子为：所谓正定算子是指§2线性空间例：量子力学中简谐振子哈密顿算子为：定义：设U是内积空间上线性变换，为U伴随变换，假如则称U为等距变换。若同时满足则称它为酉变换或么正变换。在有限维空间，变换有左逆必有右逆，所以等距与么正是等价，么正变换逆变换是它伴随变换，即二、等距变换特征因为一个变换A伴随变换在正交归一基下对应矩阵是A在同一基下对应矩阵共轭转置，故等距变换在正交归一基下对应矩阵也满