内容提供者
勾股定理的应用举例省公共课一等奖全国赛课获奖课件.pptx
2024-02-11
11金币
1MB
16页
胜利****实阿
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
亲，该文档总共16页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
勾股定理的应用举例省公共课一等奖全国赛课获奖课件.pptx
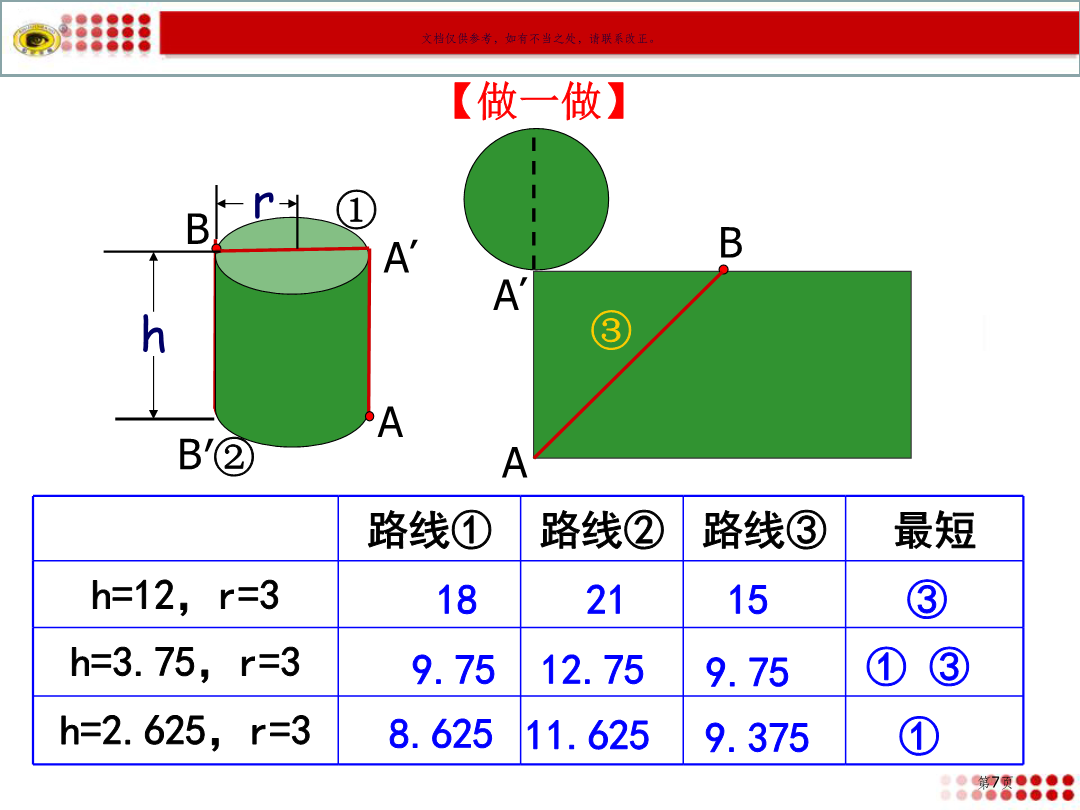
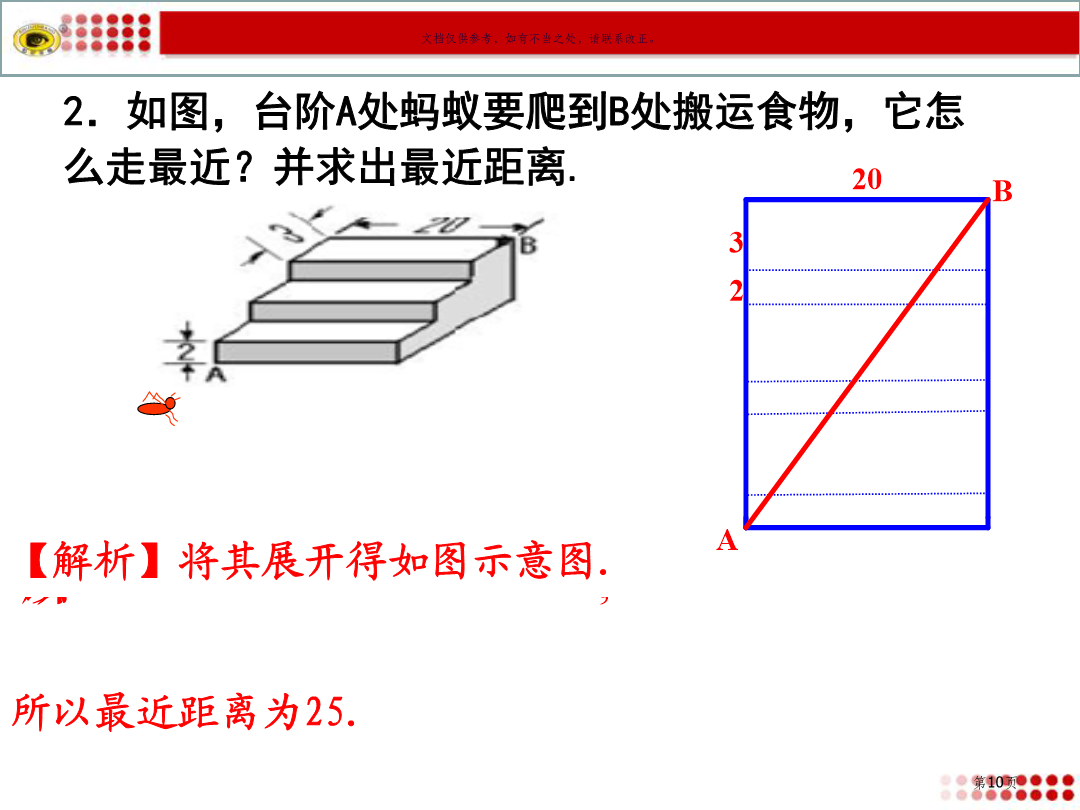
1.能利用勾股定理及直角三角形判别条件（即勾股定理逆定理）处理简单实际问题.1.你知道勾股定理内容吗？2.一个三角形三条边长分别为a,b,c(c>a,c>b），能否判断这个三角形是否是直角三角形？A我想检测雕塑底座正面AD边和BC边是否分别垂直于底边AB，随身只带了一把卷尺.（1）量得AD长是30cm，AB长是40cm，BD长是50cm.AD边垂直于AB边吗？（2）若随身只有一个长度为20cm刻度尺，能有方法检验AD边是否垂直于AB边吗？2．如图，台阶A处蚂蚁要爬到B处搬运食物，它怎么走最近？并求出最近距
2024-02-11
11
1MB
勾股定理的应用课件省公共课一等奖全国赛课获奖课件.pptx
●邮递员从车站O正东1km邮局A出发，先向正北走了3km到B，又向正西走了4km到C，最终再向正南走了6km到D，那么最终该邮递员与邮局距离为多少km？二探究探究试一试4如图，在△ABC中，AB=AC，D点在CB延长线上，求证：AD2-AB2=BD·CD如图，已知：等腰直角△ABC中，P为斜边BC上任一点.求证：PB2＋PC2＝2PA2.如图，已知：△ABC中，AD是中线，AE⊥BC于E.⑴若AB=12，BC=10，AC=8,求：DE长度.如图，已知：△ABC中，AD是中线，AE⊥BC于E.⑵求证：AB2
2024-02-11
11
1.1MB
勾股定理的应用省公共课一等奖全国赛课获奖课件.pptx
请同学们完成下面练习在一次台风攻击中，小明家房前一棵大树在离地面6米处断裂，树顶部落在离树根底部8米处。你能告诉小明这棵树折断之前有多高吗？一辆装满货物卡车，其外形高2.5米，宽1.6米，要开进厂门形状如图某工厂，问这辆卡车能否经过该工厂厂门?说明理由2.3米如图，将长为10米梯子AC斜靠在墙上，BC长为6米。一位工人叔叔要装修家，需要一块长3m、宽2.1m薄木板，已知他家门框尺寸如图所表示，那么这块薄木板能否从门框内经过?为何?一个门框尺寸如图所表示，一块长3m、宽2.1m薄木板能否从门框内经过?为何?
2024-05-27
8
541KB
勾股定理的应用省公共课一等奖全国赛课获奖课件.pptx
1、在直角三角形ABC中，两条直角边a，b分别等于6和8，则斜边c等于（）。2、直角三角形一直角边为9cm，斜边为15cm,则这个直角三角形面积为（）cm2。3、一个等腰三角形腰长为20cm，底边长为24cm，则底边上高为（）cm，面积为（）cm2。1.在一次台风攻击中，小明家房前一棵大树在离地面6米处断裂，树顶部落在离树根底部8米处。你能告诉小明这棵树折断之前有多高吗？一辆装满货物卡车，其外形高2.5米，宽1.6米，要开进厂门形状如图某工厂，问这辆卡车能否经过该工厂厂门?说明理由2.3米如图，将长为10
2024-02-11
11
597KB
勾股定理应用的省公共课一等奖全国赛课获奖课件.pptx
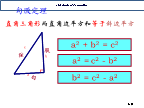
a2+b2=c2A问题一《九章算术》专设勾股章来研究勾股问题，共24个问题．按性质可分为三组，其中第一组14个问题能够直接利用勾股定理来处理．很多是含有历史地位世界著名算题．“引葭赴岸”是《九章算术》中一道题:“今有池方一丈，葭生其中央，出水一尺,引葭赴岸，适与岸齐。问水深、葭长各几何？”BC为芦苇长，AB为水深，AC为池中心点距岸边距离。《九章算术》中折竹问题：“今有竹高一丈，末折抵地，去根六尺，问折高者几何？”下列图是学校旗杆,旗杆上绳子垂到了地面,并多出了一段.一个盛饮料圆柱形杯（如图），测得内部底
2024-02-12
11
1.8MB