课件-全国-2011_中考数学专题探究课件 第四讲 图形的认识（一）.rar

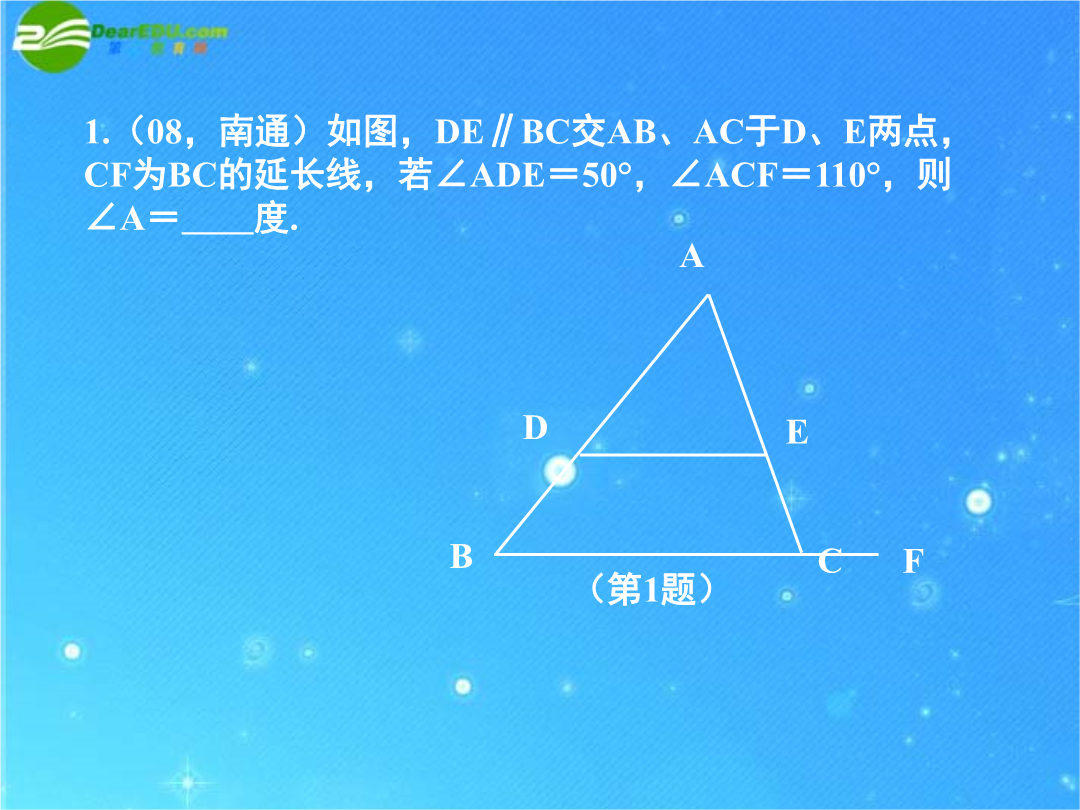
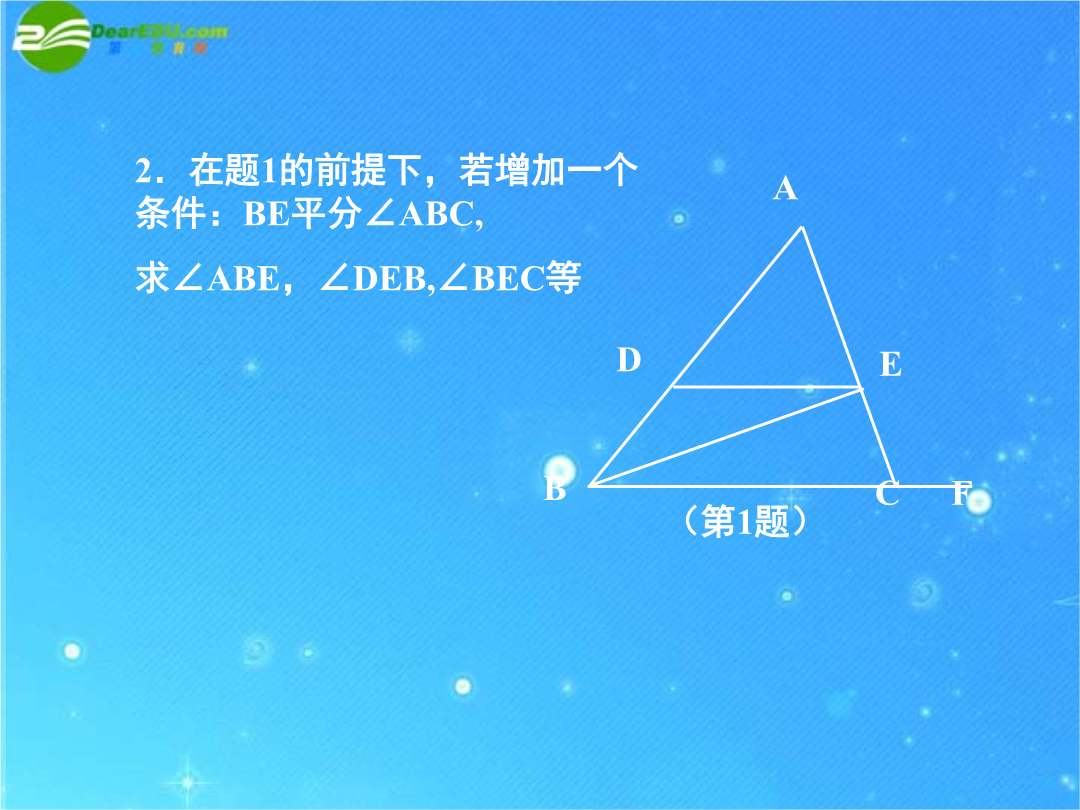
中考数学专题探究A解这类题，由于考查的知识点比较多，有：平行线，补角，三角形的内角和，角平分线，外角和定理等等；在平时的学习时，要在“准”字上多下功夫，运用“比较”的思想方法，弄清它们的联系和区别.3．（08，宿迁）已知等腰三角形的两边长分别是3和7，则它的周长为cm.4．如图，点P是等边△ABC内的一点，连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP，连接CQ.(1)观察并猜想AP与CQ之间的大小关系，并证明你的结论.（2）若PA:PB:PC=3:4:5,连接PQ，试判断△PQC的形状，并说明理由.分析：（2）连接PQ，则△PBQ是等边三角形，PQ=PB,PA=CQ，故CQ:PQ:PC=PA:PB:PC=3:4:5，所以△PQC是直角三角形.5．在下列说法中错误的是（）A．在△ABC中，∠C=∠A－∠B,则△ABC为直角三角形.B．在△ABC中，若∠A:∠B:∠C=5:2:3，则△ABC为直角三角形.C．在△ABC中，若，则△ABC为直角三角形.D．在△ABC中，若a:b:c=2:3:4，则△ABC为直角三角形.分析：A、B用角去判断，关键是确定最大角；C、D借助勾股定理的逆定理判断,关键是确定最大边.判定直角三角形的方法是：（1）当已知一个三角形的两内角度数或三角度数比时，利用定义判定.（2）当已知三边长或三边长的比时，利用勾股定理的逆定理来判定.在三角形中作高，求边长或面积.在梯形中从上底两端点作下底的高，求边长或面积.勾股定理在图形中的运用勾股定理在图形中的运用6．如图，正方形网格中，小格的顶点叫做格点，小华按下列要求作图：①在正方形网格记得三条不同的实线上各取一个格点，是其中任意两点不在同一实线上；②连接三个格点，使之构成直角三角形，小华在下面的正方形网格中作出了Rt△ABC。请你按照同样的要求，在另外两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等.分析:此题的答案可以有很多种，关键是抓住有一直角这个特征，可以根据勾股定理的逆定理“有两边的平方和等于第三边的平方，则三角形为直角三角形”构造出直角三角形.如图，已知AD∥BC,AC⊥BC于C,BD交AC于E，DE=2AB，求证：∠DBC=∠ABC.取DE的中点F，连接AF，∵AD∥BC,AC⊥BC于C,∴在Rt△ADE中，FA=DF=EF,∵DE=2AB,∴DF=AF,AF=AB,∴∠ADE=∠DAF,∠AFB=∠ABD,∴∠AFB=∠ADE+∠DAF=2∠ADE,即∠ABD=2∠ADE,又∵AD∥BC,∴∠ADE=∠DBC,∠ABC=∠ABD+∠DBC,∴∠DBC=∠ABC.8．已知：如图设AT是△ABC的角平分线，M是BC中点，ME∥AT交AB、AC或其延长线于点D、E，求证：BD=CE.证明：延长EM到点F,使FM=EM，连接BF,得∠BMF=∠CME∵M是BC中点∴BM=MC∴△EMC≌△FMB可得∠F=∠EBF=CE∵AT是△ABC的角平分线，∴∠1=∠2∵ME∥AT∴∠1=∠3,∠2=∠E,∴∠3=∠F∴BD=BF又△EMC≌△FMB可得BF=CE∴BD=CE.在寻求三角形全等的条件时：张大爷家承包了村里的鱼塘，今年获得了大丰收，他想把鱼塘的面积扩大１倍，对此，村长表示大力支持，同时又从地处旅游景区考虑提出两点建议：（１）原来鱼塘４个角的４棵树龄达３００多年的老槐树不要移动.（２）为了便于景点的美化，新鱼塘最好扩成平行四边形.张大爷在孙子小明的帮助下，设计了如图的扩建方案，你能对这一方案进行解说吗？解说：连接AC、BD,交于点O,过点A、C作BD的平行线，过点B、D作AC的平行线，分别交于点E、F、G、H，得到了四个平行四边形.由平行四边形的对角线将其分成了两个全等的三角形，可知四边形ABCD的面积扩大了1倍.对角线是把四边形转化为三角形的桥梁和纽带，是研究四边形的常见的辅助线，它既可以把四边形转化为三角形，又可以充分体现四边形的所有特征.10.（07,牡丹江）已知矩形ABCD中（AD>AB），EF经过对角线的交点O，且分别交AD、BC于E、F，请你添加一个条件：，使四边形EBFD是菱形.11．如图，在半圆O中，四边形OABC,ODEF,OGHM,都是矩形，试说明AC，DF,MG三条线段的大小关系。分析：这是一道矩形在圆中的运用，由图形观察三条线段比较零散，通过平移不容易解决问题，发现三个四边形都是矩形，想到矩形的性质，对角线相等。AC=OB,DF=OE,MG=OH,又因为OB,OE,OH都是圆的半径，所以AC=DF=MG.12．如图，4个小动物分别站在正方形场地的4个顶点，它们同时出发并以相同的速度沿场地边缘逆时针方向跑动，当它们同时停止时，依次连接4个动物所在地点，围成的图形是什么形状，为什么？13．如图，在等