
杆件结构的变形计算.ppt

胜利****实阿








亲,该文档总共109页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

杆件结构的变形计算.ppt
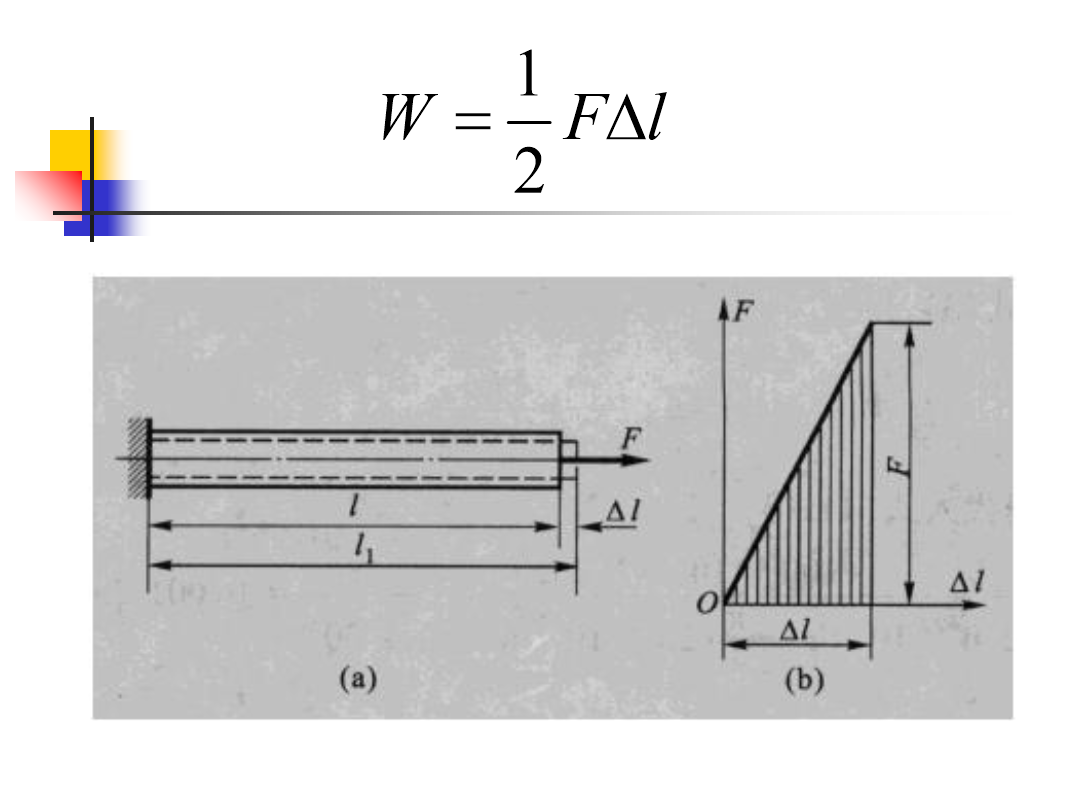
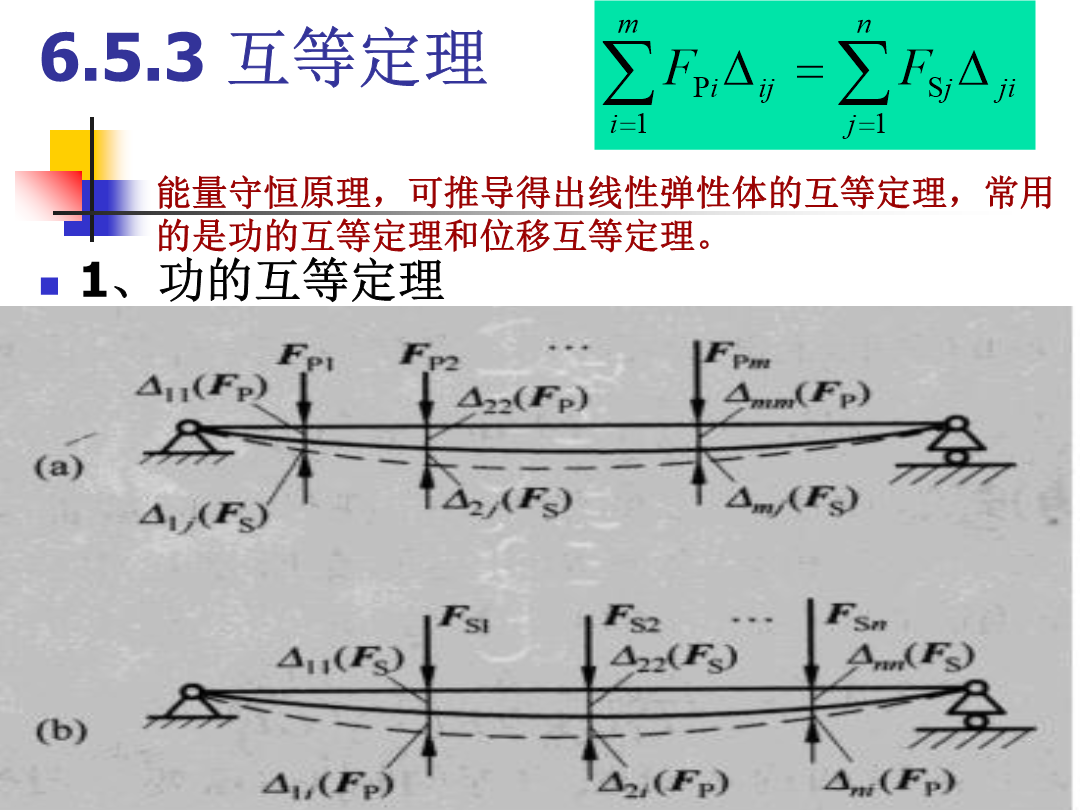
6.5能量法基础6.5.1作用在弹性杆件上的力所作的功1、常力功当杆件位移发生之前,力已经存在,且位移产生过程中,作用力不发生变化,则此时力所作的功为常力功。等于该力的大小与其作用点沿力方向相应位移的乘积。2、变力功当弹性杆件在力的作用下所产生的位移,随力和变形的增加而增加时,力所作的功为变力功。6.5.2杆件的弹性应变能若轴力6.5.3互等定理力系推导:2、位移互等定理在弹性范围内,弹性体在外力作用下发生变形而在体内积蓄的能量,称为弹性变形能,简称变形能.可变形固体在受外力作用而变形时,外力和内力均将作

杆件结构的变形计算.ppt
6.5能量法基础6.5.1作用在弹性杆件上的力所作的功1、常力功当杆件位移发生之前,力已经存在,且位移产生过程中,作用力不发生变化,则此时力所作的功为常力功。等于该力的大小与其作用点沿力方向相应位移的乘积。2、变力功当弹性杆件在力的作用下所产生的位移,随力和变形的增加而增加时,力所作的功为变力功。6.5.2杆件的弹性应变能若轴力6.5.3互等定理力系推导:2、位移互等定理在弹性范围内,弹性体在外力作用下发生变形而在体内积蓄的能量,称为弹性变形能,简称变形能.可变形固体在受外力作用而变形时,外力和内力均将作

65杆件结构的变形计算.pptx
6.5能量法基础6.5.1作用在弹性杆件上的力所作的功1、常力功当杆件位移发生之前,力已经存在,且位移产生过程中,作用力不发生变化,则此时力所作的功为常力功。等于该力的大小与其作用点沿力方向相应位移的乘积。2、变力功当弹性杆件在力的作用下所产生的位移,随力和变形的增加而增加时,力所作的功为变力功。6.5.2杆件的弹性应变能6.5.3互等定理力系2、位移互等定理在弹性范围内,弹性体在外力作用下发生变形而在体内积蓄的能量,称为弹性变形能,简称变形能.可变形固体在受外力作用而变形时,外力和内力均将作功.对于弹性

弹性杆件的变形与位移计算.doc
弹性杆件的变形与位移计算概念题1.判断题:(以下结论对者画√,错者画×)(1)杆件拉压变形时,其伸缩量只与外力、杆的材料、长度、截面积有关。()(2)梁的最大截面转角必发生在弯矩最大的截面处。()(3)若等截面直梁某一段内弯矩皆等于零,则该段梁的挠曲线必定是一直线段,因而该段梁各截面的转角皆相等。()(4)等截面梁纯弯曲时,变形后梁的挠曲线必为一圆弧线;反之,若变形后梁的挠曲线是一条圆弧线,则该梁必为纯弯曲。()(5)图示两根等截面简支梁,其材料、跨度、截面尺寸和载荷集度均相同,因而它们跨中的挠度相等。(

材料力学-杆件的变形计算.pptx
第四章杆件旳变形计算公式旳合用条件第二节圆轴旳扭转变形及相对扭转角在一段轴上,对单位长度扭转角公式进行积分,就可得到两端相对扭转角j。利用积分法求梁变形旳一般环节:⑴建立坐标系(一般:坐标原点设在梁旳左端),求支座反力,分段列弯矩方程;⑵分段列出梁旳挠曲线近似微分方程,并对其积分两次;⑶利用边界条件,连续条件拟定积分常数;⑷建立转角方程和挠曲线方程;⑸计算指定截面旳转角和挠度值,尤其注意和及其所在截面。
