MATLAB数值计算分解.pptx

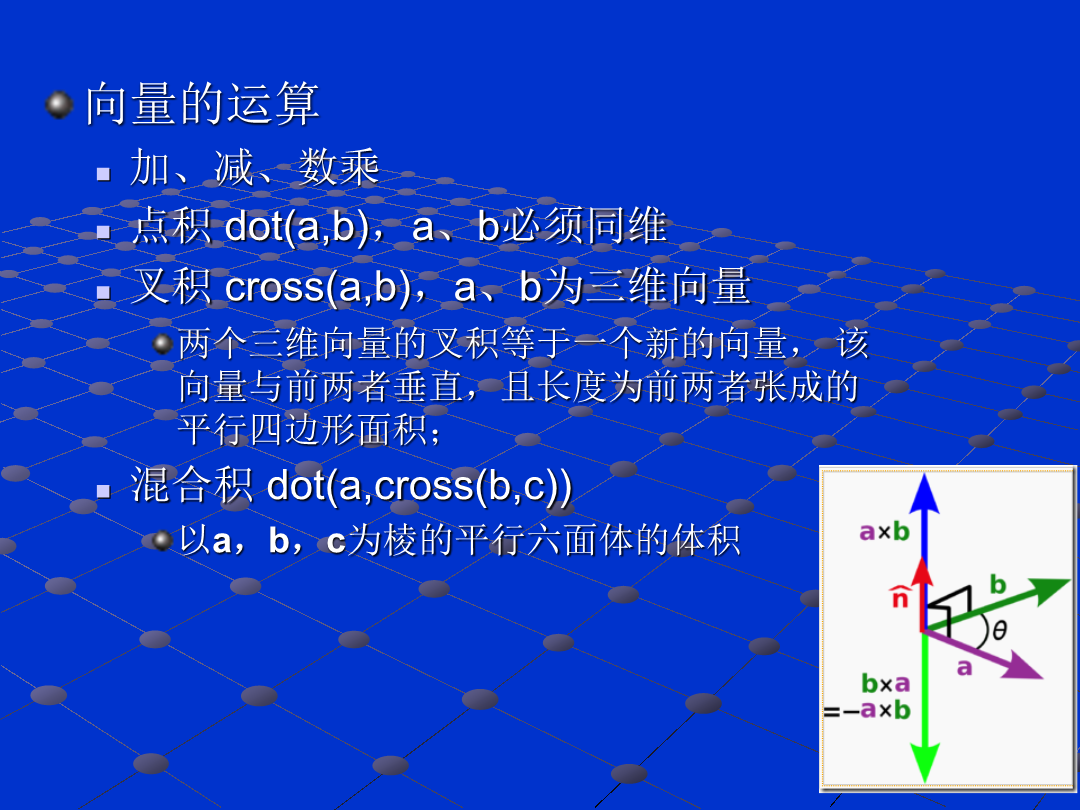
Matlab数值计算基础功能内容一、向量输入及其运算线性等分向量的生成格式：y=linspace(x1,x2,n)生成n维行向量，y(1)=x1、y(n)=x(2)若n缺省，则默认n=100对数等分向量的生成格式：y=logspace(x1,x2,n)生成n维行向量，y(1)=10^x1、y(n)=10^x(2)若n缺省，则默认n=50向量的运算加、减、数乘点积dot(a,b)，a、b必须同维叉积cross(a,b)，a、b为三维向量两个三维向量的叉积等于一个新的向量，该向量与前两者垂直，且长度为前两者张成的平行四边形面积；混合积dot(a,cross(b,c))以a，b，c为棱的平行六面体的体积二、MATLAB矩阵其他特殊矩阵函数2.4矩阵的运算2矩阵与常数间的运算常数与矩阵的各元素间进行运算，当作除法时，常数只能做除数。2.4.2矩阵的函数运算特征向量、特征值计算函数eig、eigs奇异值函数svd、svds条件数函数cond、condest、rcond特征值的条件数condeig范数函数norm、normest秩函数rank迹函数traceMATLAB在三维向量中的应用1.向量共线或共面的判断例设X=(1，1，1)，Y=(-1，2，1)，Z=(2，2，2)，判断这三个向量的共线共面问题。命令如下：X=[1,1,1];Y=[-1,2,1];Z=[2,2,2];XY=[X;Y];YZ=[Y;Z];ZX=[Z;X];XYZ=[X;Y;Z];rank(XY)rank(YZ)rank(ZX)rank(XYZ)7.点到平面的距离例求原点到平面X+Y+Z=1的距离。命令如下：u=[0,0,0];v=[1,1,1];%A=B=C=1,u1=u2=u3=0,D=-1r=abs(u*v'-1)/norm(v,2)r=0.57742.4.3矩阵分解函数特征值分解函数eig复数特征值对角阵与实数块特征值对角阵地转化cdf2rdf、rsf2csf奇异值分解svdLU分解[L,U]=lu(A)将方阵A分解为交换下三角矩阵L和上三角矩阵U，使A=LU[L,U,P]=lu(A)将方阵A分解为下三角矩阵L和上三角矩阵U，使PA=LUChol分解cholQR分解（正规正交矩阵Q与上三角形矩阵R）[Q,R]=qr(A)，根据方阵A，求一个正交矩阵Q和一个上三角矩阵R，使A=Q*R例如，对矩阵A进行QR分解的命令是：A=[2,1,-2;1,2,1;2,5,3];[Q,R]=qr(A)例：A=[2,1,4,6;1,2,1,5;4,1,3,4;6,5,4,2];[Q,D]=eig(A)Q*D*Q'ans=2.00001.00004.00006.00001.00002.00001.00005.00004.00001.00003.00004.00006.00005.00004.00002.0000结果与A相等，说明确实将A分解为了QDQ'的乘积。1、对角阵与三角阵矩阵的对角元素(1)提取矩阵的对角线元素设A为m×n矩阵，diag(A)函数用于提取矩阵A主对角线元素产生一个具有min(m,n)个元素的列向量。diag(A,k)，其功能是提取第k条对角线的元素。(2)构造对角矩阵设V为具有m个元素的向量，diag(V)将产生一个m×m对角矩阵，其主对角线元素即为向量V的元素。diag(V,k)，其功能是产生一个对角阵，其第k条对角线的元素即为向量V的元素。2、矩阵变向1.矩阵的转置转置运算符是单撇号(‘)2.矩阵的旋转rot90(A,k)，功能是将矩阵A逆时针方向旋转90º的k倍当k为1时可省略3.矩阵的左右翻转fliplr(A)4.矩阵的上下翻转flipud(A)5.第dim维翻转flipdim(A,dim)3、变维（1）reshape(x,m,n)，将矩阵x变成m*n阶（2）“：”符号例如：c(:)=a(:)两个矩阵必须预先定义维数三、矩阵的数组运算在matlab中，数组的建立、存储与矩阵相同，只是在计算时符号不同。四、多项式运算多项式运算：求值polyval(p,b)%b为数组或单个数值polyvalm(p,B)%B为方阵求根roots函数多项式乘法conv函数多项式除法deconv函数多项式微分polyder函数多项式拟合函数polyfit(x,y,n)x、y为已知数据的横坐标和纵坐标向量，n为拟合多项式的次数图像上下翻转程序结束