
第二章优化设计的数学基础.pptx

胜利****实阿






亲,该文档总共58页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

第二章优化设计的数学基础.pptx
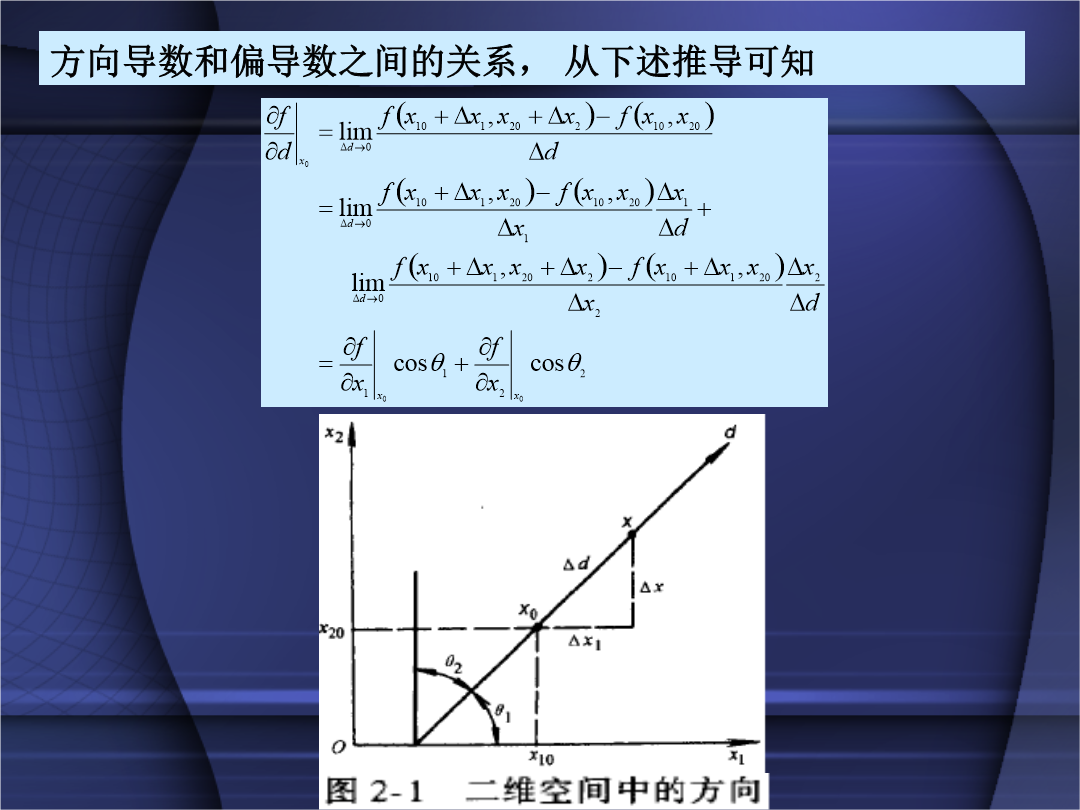
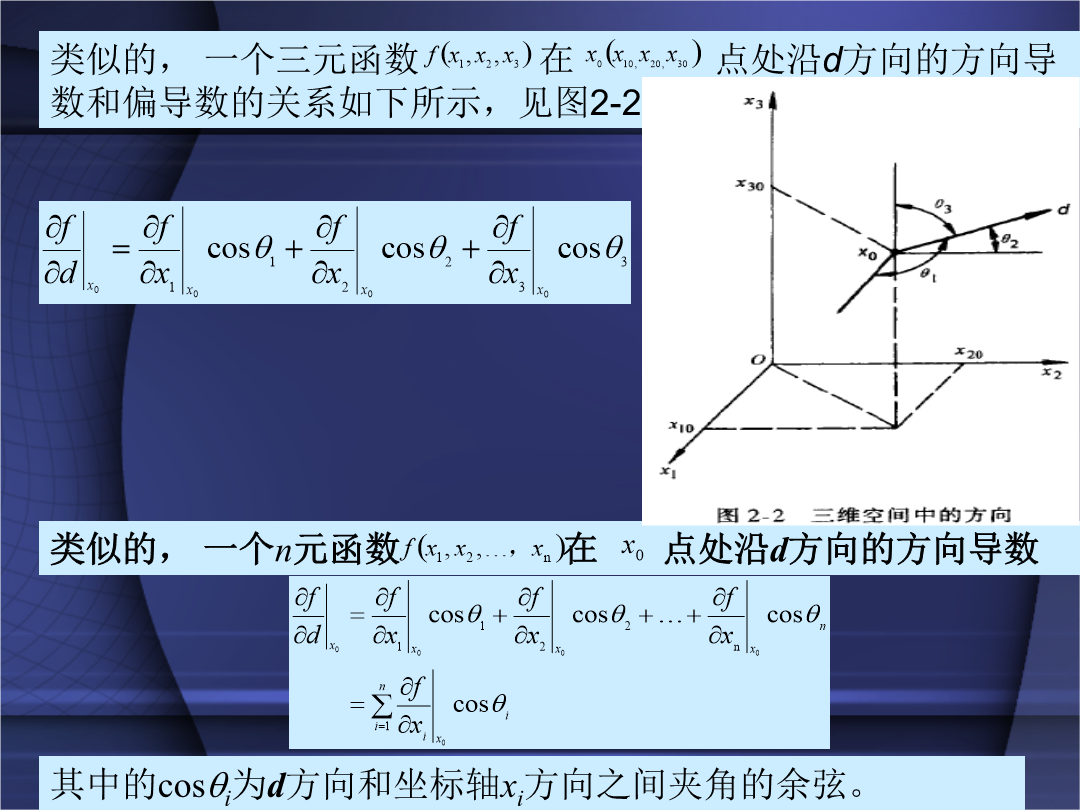
方向导数和偏导数之间的关系,从下述推导可知类似的,一个三元函数在点处沿d方向的方向导数和偏导数的关系如下所示,见图2-22、二元函数的梯度`三、向多元函数的推广函数f(x1,x2,,xn)在x0(x1,x2,,xn)处的梯度可定义为函数f(x1,x2,,xn)在x0处沿d的方向导数可表示为d方向上的单位向量梯度f(x0)的模为梯度方向单位向量为,它与函数等值面f(x)=c相垂直,也就是和等值面上过x0的一切曲面相垂直,如图2-5所示。2.2多元函数的泰勒(Taylor)展开式2.3无约束优化问题的

机械优化设计优化设计的数学基础.pptx

优化设计的数学基础.ppt
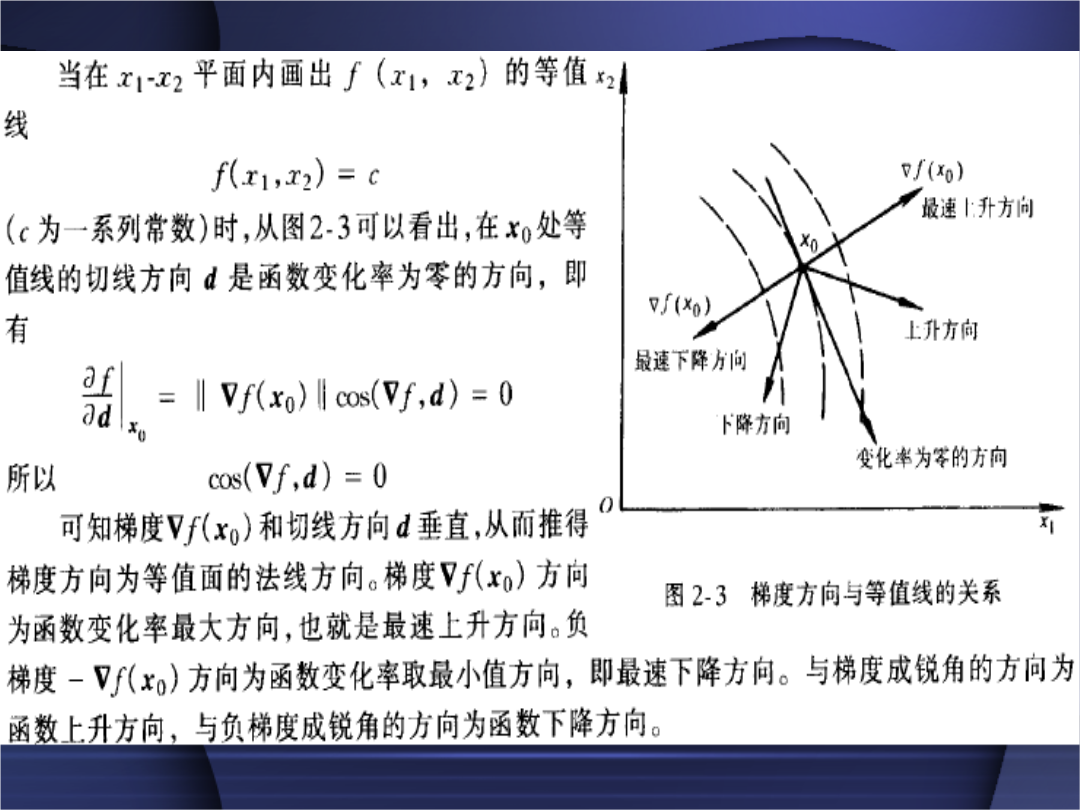
第一节多元函数的方向导数与梯度图2-1函数的方向导数其函数在点沿d方向的方向导数为二、二元函数的梯度即图2-5梯度方向与等值面的关系若目标函数f(x)处处存在一阶导数,则极值点的必要条件一阶偏导数等于零,即泰勒展开写成向量矩阵形式(1)▽F(X*)=0;必要条件(2)Hesse矩阵G(X*)为正定。充分条件同学考虑二元函数在处取得极值的充分必要条件。第四节凸集、凸函数与凸规划一、凸集称三、凸性条件设f(x)为定义在凸集R上且具有连续二阶导数的函数,则f(x)在R上为凸函数的充要条件凸规划的性质:第五节等式

优化设计的数学基础.ppt
第三章优化设计的数学模型优化设计的数学模型是描述实际优化问题的设计内容、变量关系、有关设计条件和意图的数学表达式,它反映了物理现象各主要因素的内在联系,是进行优化设计的基础。§3-1设计变量二、设计点与设计空间设计点:X(k)(x1(k),x2(k),…,xn(k)):是设计向量X(k)的端点,代表设计空间中的一个点,也代表第k个设计方案。可能是可行方案、也可能不是可行方案。设计空间Rn:以x1,x2,…,xn为坐标轴,构成n维欧氏实空间Rn。它包含了所有可能的设计点,即所有设计方案。三、连续量与离散量一

02 优化设计的数学基础.ppt
第二章优化设计中绝大多数是多变量有约束的非线性规划问题,即是求解多变量非线性函数的极值问题。由此可见,优化设计是建立在多元函数的极值理论基础上的,对于无约束优化问题为数学上的无条件极值问题,而对于约束优化问题则为数学上的条件极值问题。为便于后续各章优化方法的学习,有必要研究这些非线性函数的性质和变化规律。2.1函数的泰勒(Taylor)表达式工程设计的优化问题中,所列的目标函数往往很复杂,为了简化问题,常将目标函数在所讨论点附近展开成泰勒多项式来近似原函数。一元函数f(x)在点X(k)的某个领域内具有直到
