第二章电子计算机中信息的表示及其运算.ppt

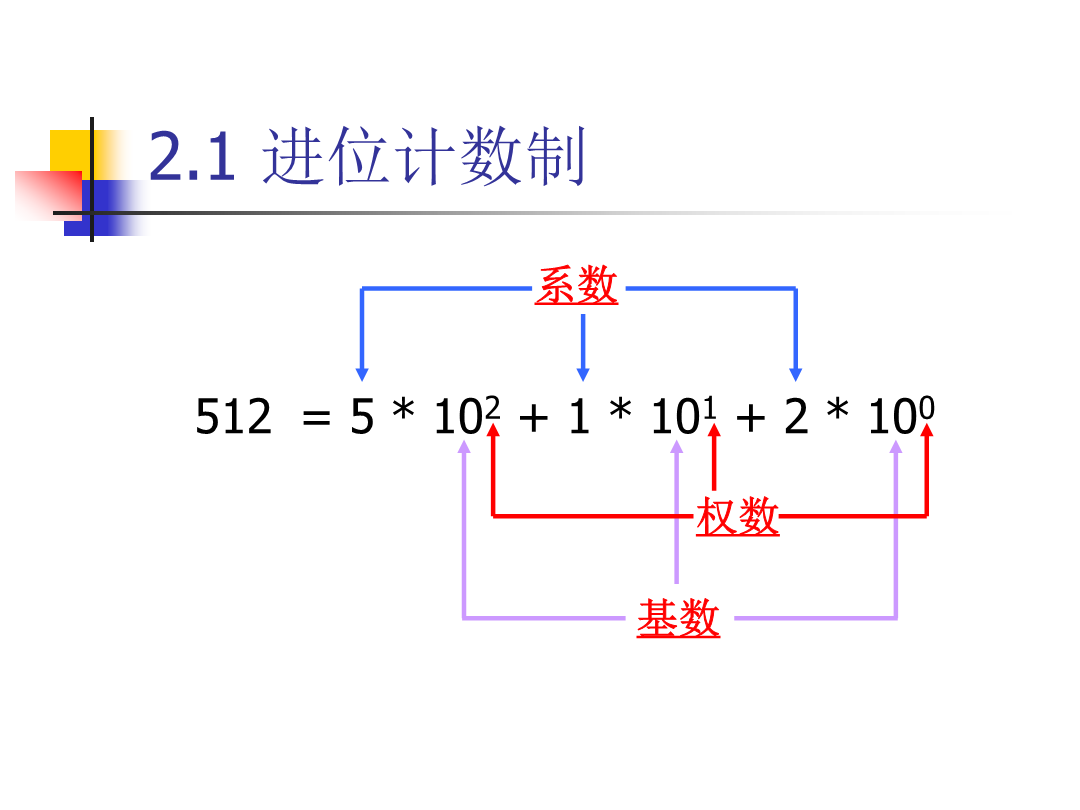
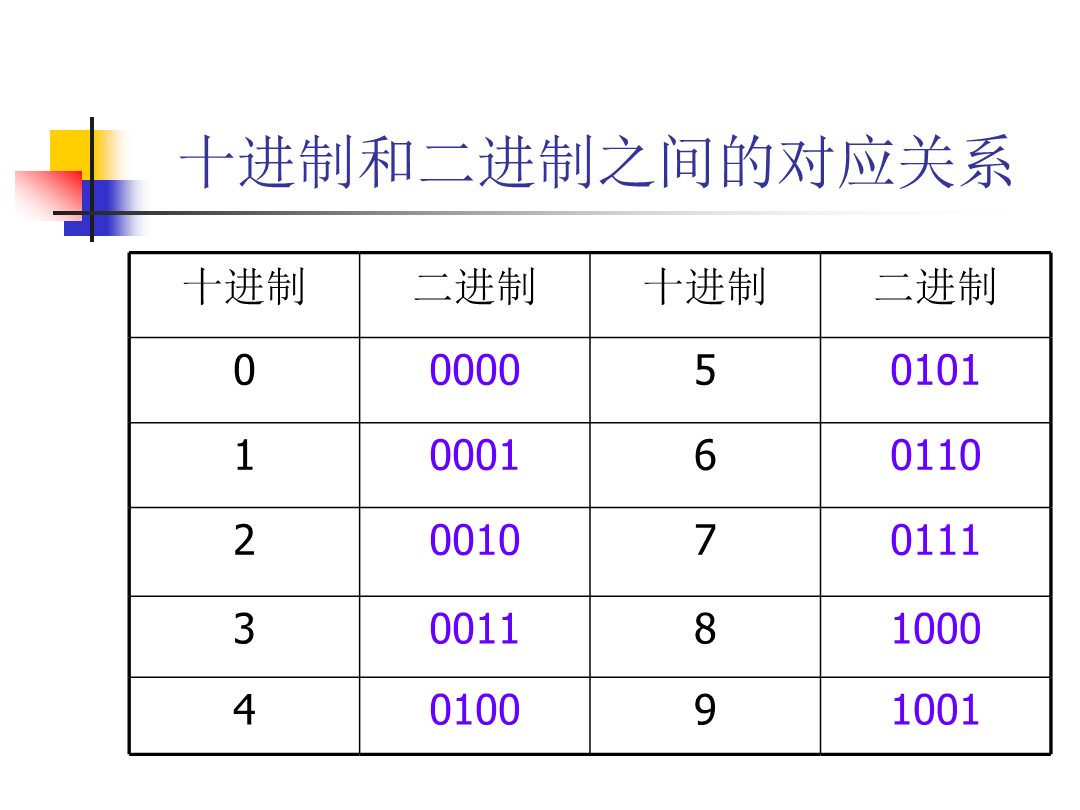
第二章电子计算机中信息的表示及其运算2.1进位计数制2.1.1概述进位计数制的表示方法假设有一数值NN=(dn-1dn-2……d1d0d-1……d-m)rN=dn-1rn-1+dn-2rn-2+……d1r1+d0r0+d-1r-1+……+d-mr-mr:基值di:系数r:为权数m,n:正整数，分别表示小数位和整数位例2-1-1例2-1-1二进制权数：2n-1，2n-2…………系数：0，1基数：r=2表示方法：在数字的末尾加上一个字母B例如：331.25=101001011.01B注:十进制数在数字的末尾加上一个字母D十进制例2-1-2二进制数的优缺点优点二进制数便于物理元件的实现二进制数运算简单二进制数使用器材少便于实现逻辑运算缺点代码冗长不便阅读八进制(Octal)和十六进制(Hexadecimal)八进制权数：8n-1，8n-2系数：0，1，2，3，4，5，6，7基数：r=8表示方法：在数字的末尾加上一个字母O例如：331.25=513.2O八进制(Octal)和十六进制(Hexadecimal)八进制权数：8n-1，8n-2系数：0，1，2，3，4，5，6，7基数：r=8表示方法：在数字的末尾加上一个字母O例如：331.25=513.2O十进制和八进制之间的对应关系例2-1-3例2-1-4十六进制权数：16n-1，16n-2，…………系数：0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F基数：r=16表示方法：在数字的末尾加上一个字母H例如：331.25=14B.4H十进制例2-1-5例2-1-52.1.2不同计数制之间的转换例2-1-7将(732.6)八转换成十进制数基值重复相乘（相除）法整数的基值反复相乘法设N是一个四位的二进制数运算步骤从最高为开始，将最高为乘以2，加上次高位，令结果为M1M1乘以2，加上第三位，令结果为M2M2乘以2，加上第四位，令结果为M3，按这种方法一直运算下去，加到最低位为止最后，所得到的结果就是转换的结果例2-1-8将(101101)二转换成十进制数例2-1-8将(101101)二转换成十进制数小数的基值反复相除法设N为四位的二进制小数运算步骤从最低位开始，将最低位除以2，加上次低位，令结果为R1R1除以2，加上第三低位，令结果为R2R2除以2，加上第四低位，令结果为R3，一直进行到小数点左边的0为止所得到的十进制小数就是所要求的结果例2-1-9将N=(0.1011)二转换为十进制小数例2-1-10将N=(632.43)八转换为十进制小数将十进制数转换成其它进位制数将十进制数转换成二进制数整数部分的转换小数部分的转换将十进制数转换成其它进位制数将十进制数转换成二进制数整数部分的转换小数部分的转换例2-1-11求十进制数43的二进制表示例2-1-12求(0.6875)十的二进制小数值例2-1-13求(0.423)十的二进制小数值（精度为2-5）将十进制转换成其它进位制数例2-1-14将(0.6328125)十转换成八进制数例2-1-15将(3952)十转换成十六进制数例2-1-15将(3952)十转换成十六进制数二进制与八进制、十六进制数之间的转换二进制--〉八进制二进制十六进制真值与机器数真值：用“+”，“-”来表示符号“正”、“负”的二进制数机器数：用“0”，“1”来表示符号“正”、“负”的二进制数数据编码根据用途不同：原码、补码、反码为了方便人机交互有权码：8421码、2421码、5421码……无权码：余3码、格雷码……检测能力的数据编码：奇偶校验码、五中取二码纠错能力的数据编码：汉明码、倍数正误码数字、字母、字符编码：ASCII码、EBCDIC码、汉字编码带符号数与不带符号数带符号数与不带符号数定点与浮点表示定点数纯小数：小数点固定在符号位之后，如1.1010111，此时机器中所有的数都是小数。纯整数：小数点固定在最低位之后，如11010111.，此时机器中所有的数都是整数。例2-2-1例2-2-2求329.625D和54.75D之和浮点表示法为什么要用浮点表示法计算机处理的数据不一定是纯小数或者纯整数如：圆周率3.1415926有些数据的数之范围相差很大，不能用定点小数或者定点整数表示，但均可用浮点整数表示。如：电子的质量9*10-28克数学表示数学表示N=11.0101=0.110101*210=1.10101*201=1101.01*2-10=0.00110101*2100……………………………浮点机中数的表示形式规格化数非规格化数例2-2-3将N1=11.0101表示成浮点数例2-2-4将N2=0.00110101表示成浮点数例2-2-3将N1=11.0101表示成浮点数例2-2-4将N2=0.00110101表示成浮点数定点表示法与浮点表示法的比较数的表示范