
仓库容量有限条件下的随机存贮管理模型--全国研究生数学建模竞赛优秀.pdf

是丹****ni








在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

仓库容量有限条件下的随机存贮管理模型--全国研究生数学建模竞赛优秀.pdf
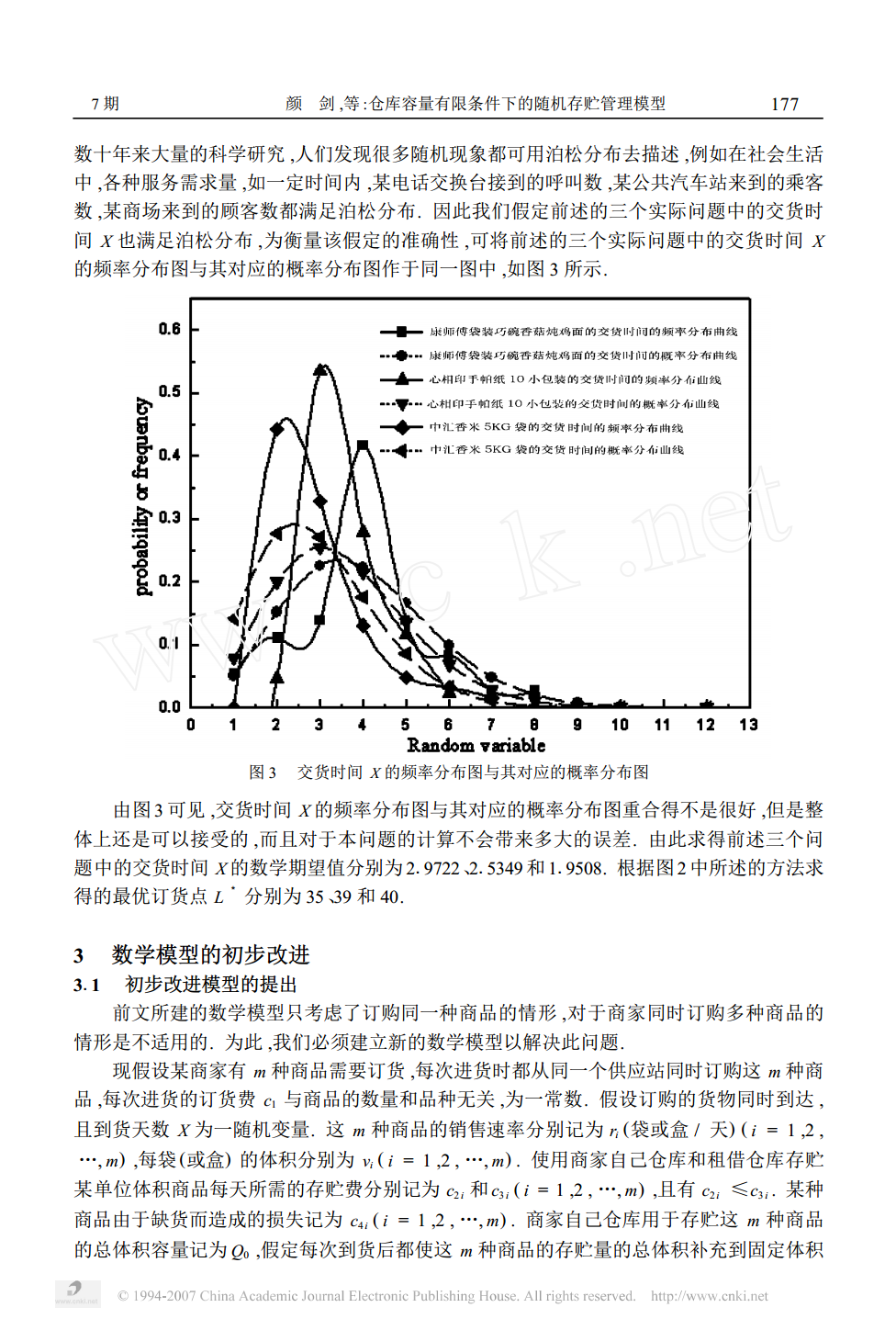
第36卷第7期数学的实践与认识Vol136No172006年7月MATHEMATICSINPRACTICEANDTHEORYJuly,2006仓库容量有限条件下的随机存贮管理模型颜剑1,周伶玲1,刘伟2(1.中南大学材料科学与工程学院,湖南长沙410083)(2.中南大学化学化工学院,湖南长沙410083)摘要:以商场的商品销售与存贮为研究对象,建立了一类在仓库容量有限条件下的存贮管理决策模型,并给出了最优存贮策略.针对某个大型超市的三种商品的真实销售数据,我们运用该模型分析求解得出了三种商品的最优订货点

仓库容量有限条件下的随机存贮管理模型--全国研究生数学建模竞赛优秀.pdf
第36卷第7期数学的实践与认识Vol136No172006年7月MATHEMATICSINPRACTICEANDTHEORYJuly,2006仓库容量有限条件下的随机存贮管理模型颜剑1,周伶玲1,刘伟2(1.中南大学材料科学与工程学院,湖南长沙410083)(2.中南大学化学化工学院,湖南长沙410083)摘要:以商场的商品销售与存贮为研究对象,建立了一类在仓库容量有限条件下的存贮管理决策模型,并给出了最优存贮策略.针对某个大型超市的三种商品的真实销售数据,我们运用该模型分析求解得出了三种商品的最优订货点

仓库容量有限条件下的随机存贮管理模型--全国研究生数学建模竞赛优秀.pdf
111133第36卷第7期数学的实践与认识Vol36No7

仓库容量有限条件下的随机存贮管理模型--全国研究生数.pdf
第36卷第7期数学的实践与认识Vol136No172006年7月MATHEMATICSINPRACTICEANDTHEORYJuly,2006仓库容量有限条件下的随机存贮管理模型颜剑1,周伶玲1,刘伟2(1.中南大学材料科学与工程学院,湖南长沙410083)(2.中南大学化学化工学院,湖南长沙410083)摘要:以商场的商品销售与存贮为研究对象,建立了一类在仓库容量有限条件下的存贮管理决策模型,并给出了最优存贮策略.针对某个大型超市的三种商品的真实销售数据,我们运用该模型分析求解得出了三种商品的最优订货点

数学建模y05D仓库容量有限条件下的随机存贮管理-王智勇.pdf
徐州空军学院:王智勇,冯达,段建国1、问题分析工厂生产需要定期地订购各种原料,商家销售要成批地购进各种商品。无论是原料或商品,都是一个怎样存贮的问题。存得少了无法满足需求,影响利润;存得太多,存贮费用就高。因此说存贮管理是降低成本、提高经济效益的有效途径和方法。根据存贮管理原理以及存贮费、订货费和缺货费的意义可知,为了保持一定的库存,要付出存贮费;为了补充库存,要付出订货费;当存贮不足发生缺货时,要付出缺货损失费。这三项费用之间是相互矛盾、相互制约的。存贮费与物资的数量和时间成正比,如降低存贮量,缩短存贮
