
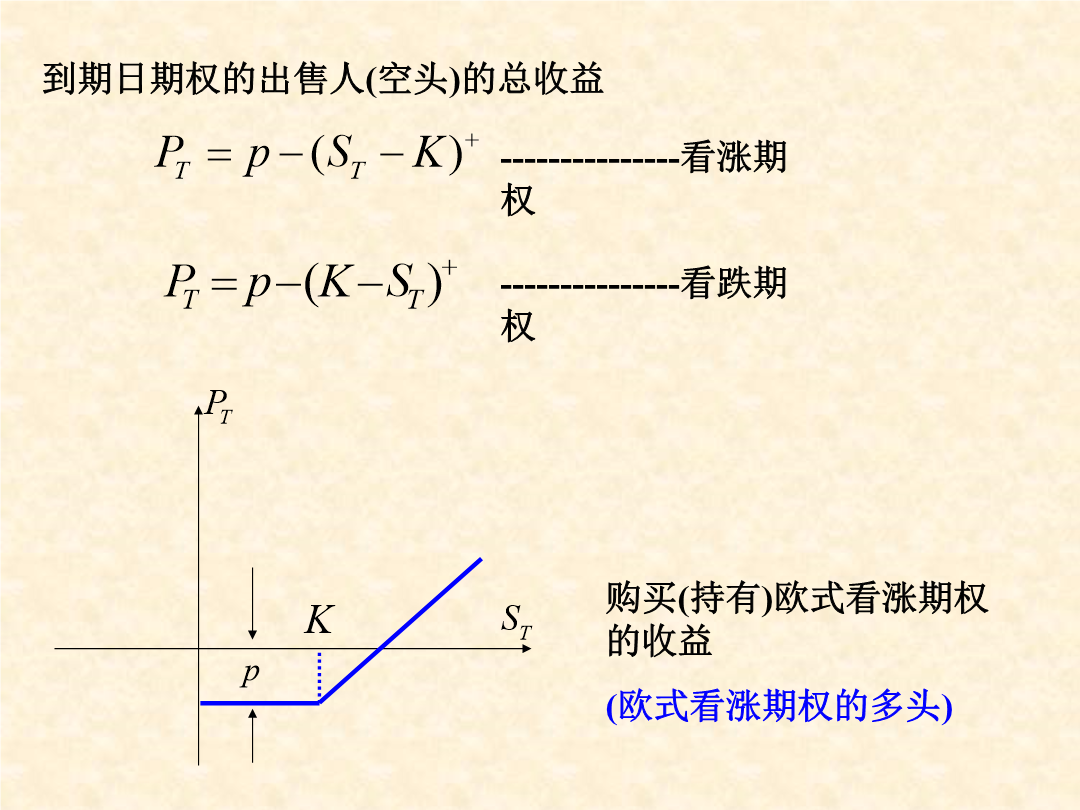
欧式期权定价.ppt

努力****晓骞








亲,该文档总共84页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

欧式期权定价.ppt
期权市场概述例如一个投资者购买一份基于DELL股票的期权合约该期权合约规定投资者在支付140美元的期权费之后就可以获得在一个月后以32.5美元/每股的价格买入100股DELL股票的权利。到时候如果DELL股票的价格高于32.5美元这个投资者就可以执行期权以32.5美元/每股的价格买入100股DELL股票从中获利显然这时DELL股票价格越高越好;如果DELL股票价格低于32.5美元该投资者就可以放弃执行期权他的全部损失就是最初支付的每股1.4美元的期权费。

欧式期权定价.ppt
期权市场概述例如一个投资者购买一份基于DELL股票的期权合约该期权合约规定投资者在支付140美元的期权费之后就可以获得在一个月后以32.5美元/每股的价格买入100股DELL股票的权利。到时候如果DELL股票的价格高于32.5美元这个投资者就可以执行期权以32.5美元/每股的价格买入100股DELL股票从中获利显然这时DELL股票价格越高越好;如果DELL股票价格低于32.5美元该投资者就可以放弃执行期权他的全部损失就是最初支付的每股1.4美元的期权费。

欧式期权定价.ppt
期权市场概述例如,一个投资者购买一份基于DELL股票的期权合约,该期权合约规定,投资者在支付140美元的期权费之后,就可以获得在一个月后以32.5美元/每股的价格买入100股DELL股票的权利。到时候,如果DELL股票的价格高于32.5美元,这个投资者就可以执行期权,以32.5美元/每股的价格买入100股DELL股票,从中获利,显然这时DELL股票价格越高越好;如果DELL股票价格低于32.5美元,该投资者就可以放弃执行期权,他的全部损失就是最初支付的每股1.4美元的期权费。而对于这个期权的卖方来说,如果

欧式期权定价.ppt
期权市场概述例如,一个投资者购买一份基于DELL股票的期权合约,该期权合约规定,投资者在支付140美元的期权费之后,就可以获得在一个月后以32.5美元/每股的价格买入100股DELL股票的权利。到时候,如果DELL股票的价格高于32.5美元,这个投资者就可以执行期权,以32.5美元/每股的价格买入100股DELL股票,从中获利,显然这时DELL股票价格越高越好;如果DELL股票价格低于32.5美元,该投资者就可以放弃执行期权,他的全部损失就是最初支付的每股1.4美元的期权费。而对于这个期权的卖方来说,如果

欧式期权的定价(常用版).doc
欧式期权的定价(常用版)(可以直接使用,可编辑完整版资料,欢迎下载)分类号________________论文选题类型UDC编号本科毕业论文(设计)题目欧式期权的定价学院物理科学与技术学院专业数学物理交叉实验班年级2021级学生姓名李林学号2021214203指导教师严国政二○一六年三月华中师范大学学位论文原创性声明本人郑重声明:所呈交的学位论文是本人在导师指导下独立进行研究工作所取得的研究成果。除了文中特别加以标注引用的内容外,本论文不包含任何其他个人或集体已经发表或撰写的成果作品。本人完全意识到本声明
